Bộ 10 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án (Đề 4)
17 câu hỏi
Điều kiện xác định của phương trình \(\frac{1}{{x\left( {{x^2} + 4} \right)}} = \frac{{x + 1}}{x} - \frac{1}{{x - 2}}\) là
\(x \ne 0,\,\,\;x\; \ne \; - 2\)và \(x \ne 2.\)
\(x \ne 0\) và \(x \ne - 2.\)
\(x \ne 0\)và \(x \ne - 4.\)
\(x \ne 0\) và \(x \ne 2.\)
Phương trình \[2x(3x - 1) + 6x - 2 = 0\] có nghiệm là
\[\left\{ {\frac{1}{3}} \right\}\].
\[\left\{ {\frac{1}{3}; - 1} \right\}\].
\[\left\{ { - 1} \right\}\].
\(\left\{ {1; - \frac{1}{3}} \right\}\)
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
\[5x - 3z = 6\].
\(5x - 8y = 0.\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Hệ phương trình nào có cùng cặp nghiệm với hệ phương trình \[\left\{ \begin{array}{l}5x + 4y = 1\\3x - 2y = 5\end{array} \right.\] ?
\[\left\{ \begin{array}{l}3x + 2y = 1\\x + y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x + 2y = 1\\x - y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x - 2y = 1\\x + y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x - 2y = 1\\x - y = 0\end{array} \right..\]
Nếu \(a,\,\,b,\,\,c\) là ba số mà \(a < b\) và \(ac > bc\) thì \(c\) là</>
số âm.
số dương.
số 0.
số tùy ý.
Với \(a > b\), chọn khẳng định sai trong các khẳng định dưới đây ?
\(a - 2 > b - 2.\)
\( - 5a > - 5b.\)
\(2a + 3 > 2b + 3.\)
\(10 - 4a < 10 - 4b.\)
Nghiệm của bất phương trình \[3\left( {x + 2} \right) \le x - 8\] là
\(x \le - 7.\)
\(x \le 7.\)
\(x \ge - 7.\)
\(x < - 7.\)
Bất phương trình nào dưới đây có nghiệm \(x \ge - \frac{3}{4}\)?
\(\frac{1}{2} + \frac{x}{3} \ge \frac{1}{4}.\)
\(3 - 0,2x < 13.\)
\(5 + 7x \ge 15.\)
\(2x - 3 \ge x + 2.\)
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha .\) Tỉ số \(\frac{{HA}}{{BA}}\) bằng:
\(\sin \alpha \).
\[\cos \alpha \].
\(\tan \alpha \).
\(\cot \alpha \).
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng:
\(\frac{{AC}}{{BC}}.\)
\(\frac{{BC}}{{AC}}.\)
\(\frac{{AB}}{{BC}}.\)
\(\frac{{AB}}{{AC}}.\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH.\) Biết \(AB = 2,5\), \(BH = 1,5.\) Số đo góc \(\widehat B\) là
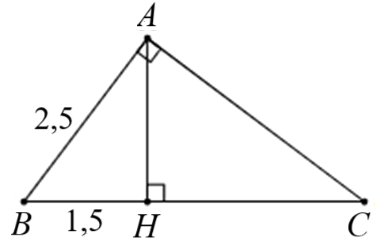
\(\widehat B = 30^\circ .\)
\(\widehat B = 53^\circ 1'.\)
\(\widehat B = 35^\circ 1'.\)
\(\widehat B = 50^\circ .\)
Cho tam giác\(ABC\)vuông tại\(A\)có \(AB = 2,5,\,\,\widehat B = 60^\circ .\) Cạnh \(AC\) có độ dài gần nhất với kết quả nào dưới đây?
\(4,33\).
\({\rm{3,4}}{\rm{.}}\)
\({\rm{1,44}}{\rm{.}}\)
\(1,3.\)
(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}x - y = 16\\2x - 5y = - 28;\end{array} \right.\]
b) \[\left\{ \begin{array}{l}x + y = 3\\3x - y = 5\end{array} \right.\];
(2,5 điểm) Giải phương trình và bất phương trình sau:
1. Giải các phương trình sau:
a) \[4x\left( {x - 3} \right) - 3x + 9 = 0\];
b) \(\frac{{12}}{{1 - 9{x^2}}} = \frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}};\)
2. Giải các bất phương trình sau:
a) \(3x - 8 > 4x - 12;\)
b) \[\frac{{2x - 1}}{3} - \frac{{x + 2}}{2} < \frac{{5x + 4}}{6};\]
e) \(2x - \frac{{x - 7}}{3} < 9.\)
(1 điểm) Trong kì thi vào THPT, hai trường A và B có tổng cộng \(500\) học sinh dự thi. Kết quả hai trường đó có \(420\) học sinh trúng tuyển. Trường A có \(80\% \) học sinh trúng tuyển, trường B có \(90\% \) học sinh trúng tuyển. Hỏi mỗi trường có bao nhiêu học sinh trúng tuyển.
(2,0 điểm)
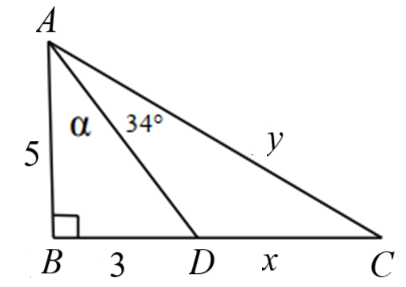
1. Cho hình vẽ bên. Tính số đo góc \(\alpha \) và các độ dài \(x,y\) (góc làm tròn đến độ, độ dài làm tròn đến hàng phần trăm).
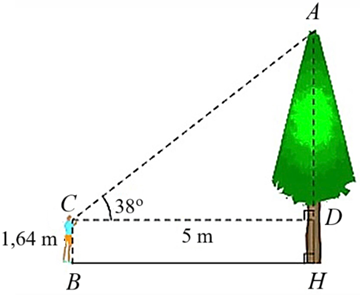
2) Để ước lượng chiều cao trong trường, bạn An đứng ở sân trường (theo phương thẳng đứng), mắt bạn An đặt tại vị trí điểm \(C\) cách mặt đất một khoảng \(CB = DH = 1,64{\rm{ m}}\)và cách cây một khoảng \(CD = BH = 5{\rm{ m}}\). Tính chiều cao \(AH\) của cây (làm tròn kết quả đến hàng phần trăm của mét), biết góc nhìn \(\widehat {ACD}\) bằng \(38^\circ \) được minh họa ở hình bên.
(0,5 điểm) Giải bất phương trình ẩn \[x\] sau: \[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} > a + b + c\] với \[a,\,\,b,\,\,c > 0\].








