Bộ 10 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án (Đề 3)
14 câu hỏi
Điều kiện xác định của phương trình \(\frac{1}{{x - 3}} - 3 = \frac{2}{{\left( {x - 3} \right)\left( {x + 4} \right)}}\) là
\[x \ne 4;{\rm{ }}x \ne - 3\].
\[x \ne 3;{\rm{ }}x \ne - 4\].
\[x \ne 3;{\rm{ }}x \ne 6\].
\[x \ne 0;{\rm{ }}x \ne - 3\].
Phương trình \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\) có nghiệm là
\[\left\{ { - 9;4} \right\}.\]
\[\left\{ 4 \right\}.\]
\[\left\{ { - 9} \right\}.\]
\[\left\{ {9;4} \right\}.\]
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}3x + 4y = 42\\10x - 9y = 6\end{array} \right.?\]
\[\left( {6;\,\, - 6} \right)\].
\[\left( {6;\,\,6} \right)\].
\[\left( { - \frac{{354}}{{13}};\,\,\frac{{402}}{{13}}} \right)\].
\[\left( {\frac{{354}}{{13}};\,\,\frac{{402}}{{13}}} \right)\].
Nếu \(a,\,\,b,\,\,c\) là ba số mà \(a < b\) và \(ac > bc\) thì \(c\) là</>
số âm.
số dương.
số 0.
số tùy ý.
Với ba số \(a,b\) và \(c < 0\), các khẳng định sau khẳng định nào đúng</>?
Nếu \[a > b\] thì \(ac > bc.\)
Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
Nếu \(a > b\) thì \(ac < bc.\)
Nếu \(a > b\) thì \(a + c < b + c.\)
Bất phương trình \[2x - 1 \le x + 4\] có nghiệm là
\[x \le 5.\]
\[x \ge 5.\]
\[x \le - 5.\]
\[x < 5.\]
Nghiệm \[x = 5\] thỏa mãn bất phương trình nào dưới đây?
\[5 + 7x \le 11.\]
\[2,5x - 6 > 9 + 4x.\]
\[5 + 7x \ge 15.\]
\[3 - 0,2x > 13.\]
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng:
\(\frac{{AC}}{{BC}}.\)
\(\frac{{BC}}{{AC}}.\)
\(\frac{{AB}}{{BC}}.\)
\(\frac{{AB}}{{AC}}.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?
\(12,45\)cm.
\(15,56\,\,{\rm{cm}}{\rm{.}}\)
\(6,43\,\,{\rm{cm}}{\rm{.}}\)
\(8\)cm.
(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}2x + 5y = 8\\2x - 3y = 0\end{array} \right.\];
b) \[\left\{ \begin{array}{l}2x + y = 4\\5x - y = 10\end{array} \right.\].
(2,5 điểm)
1. Giải các phương trình sau:
a) \[2x(3x - 1) + 6x - 2 = 0\];
b) \(\frac{2}{{x - 3}} - \frac{3}{{x + 3}} = \frac{{3x + 5}}{{{x^2} - 9}}\).
2. Giải các bất phương trình sau:
a) \(3x - 8 > 4x - 12;\)
b) \(\frac{2}{3}\left( {2x + 3} \right) < 7 - 4x;\)
c) \(2x + 3\left( {x + 1} \right) > 5x - \left( {2x - 4} \right).\)
(1 điểm) Một xe máy khởi hành cùng một lúc với hai tỉnh cách nhau \(200{\rm{ km,}}\) đi ngược chiều và gặp nhau sau 2 giờ. Tìm vận tốc của ô tô và xe máy, biết rằng nếu vận tốc của ô tô tăng thêm \(10{\rm{ km/h}}\)và vận tốc của xe máy giảm đi \(5{\rm{ km/h}}\) thì vận tốc của ô tô bằng 2 lần vận tốc của xe máy.
(2 điểm)
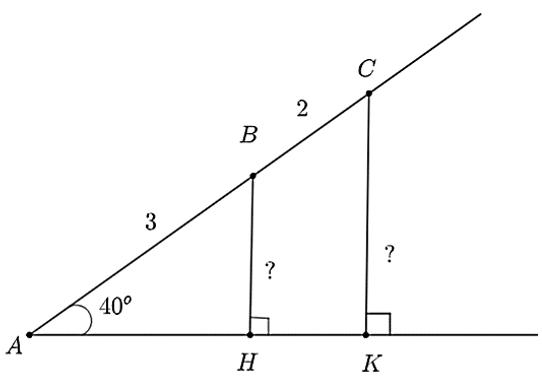
1. Cho hình vẽ dưới đây, tính độ dài các cạnh \(BH,CK,AK.\) (kết quả được làm tròn đến hàng phần mười).
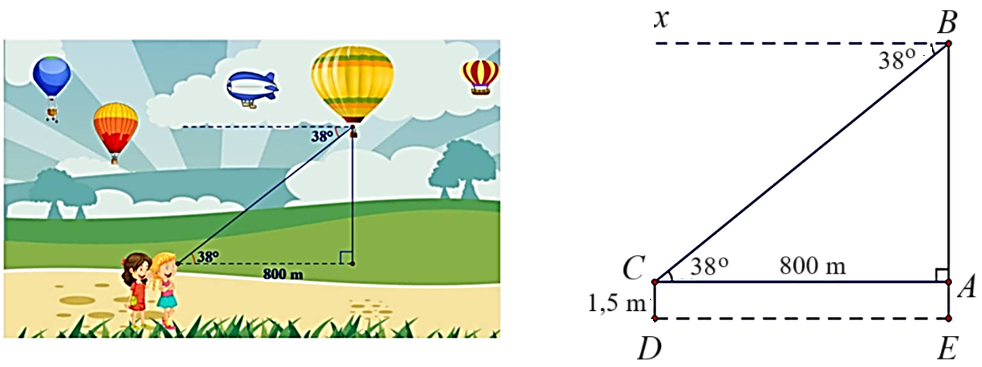
2. Một người đứng cách nơi thả khinh khí cầu 800 m nhìn thấy nó với góc nghiêng \(38^\circ .\) Tính độ cao của khinh khí cầu so với mặt đất. Cho biết khoảng cách từ mặt đất đến mắt người đó là \(1,5\,\,{\rm{m}}\) (kết quả làm tròn đến hàng phần mười).
(0,5 điểm) Cho các số thực dương \(x,\,\,y,\,\,z\) thỏa mãn \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 4.\) Chứng bất đẳng thức sau:
\(\frac{1}{{2x + y + z}} + \frac{1}{{x + 2y + z}} + \frac{1}{{x + y + 2z}} \le 1.\)








