Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án - Đề 4
38 câu hỏi
Trong các biểu thức sau, biểu thức nào là đơn thức?
\(\frac{1}{x} + y\).
\( - \frac{{{x^2}z}}{5}\).
\(\left( {2 - x} \right){y^2}\).
\(\sqrt {xyz} \).
Khi nhân đa thức \(M + N\) với đa thức \(P\)ta được kết quả là
\[MP + NP\].
\[MP + N\].
\[MN + NP\].
\[M + NP\].
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\).
Đơn thức \(B\) và đơn thức \(C\).
Đơn thức \(A\) và đơn thức \(B\).
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Giá trị của biểu thức \(A = {x^4} + 4{x^2}y - 6z\) tại \(x = 4,y = - 5,z = - 2\) là
\( - 76\).
\( - 52\).
\( - 25\).
\(37\).
Cho \({x^3} + 12{x^2} + 48x + 64 = {\left( {x + a} \right)^3}\). Giá trị của \(a\) là
\( - 64\).
64.
\( - 4\).
4.
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
\(7xy\left( {2x - 3y + 4xy} \right)\).
\(xy\left( {14x - 21y + 28xy} \right)\).
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
Phân thức nào sau đây không phải là phân thức đối của phân thức \(\frac{{1 - x}}{x}\)?
\( - \frac{{1 - x}}{x}\).
\(\frac{{ - \left( {1 - x} \right)}}{x}\).
\(\frac{{x - 1}}{x}\).
\(\frac{{x + 1}}{x}\).
Mẫu thức chung của hai phân thức \(\frac{{3x}}{{{x^2} - 4}}\) và \(\frac{x}{{x + 2}}\) là
\[{x^2} - 4\].
\[x + 2\].
\[x - 2\].
\[\left( {{x^2} - 4} \right)\left( {x + 2} \right)\].
Hình chóp tam giác đều có bao nhiêu mặt?
3.
4.
5.1
6.
Đặc điểm nào sau đây là sai đối với hình chóp tam giác đều \(S.ABC?\)
Đáy \(ABC\) là tam giác đều.
\(SA = SB = SC\).
Tam giác \(SBC\) là tam giác đều.
\(\Delta SAB = \Delta SBC = \Delta SCA\).
Cho tam giác \(ABC\) vuông có cạnh huyền \(AB = \sqrt {117} \;\;{\rm{cm}}{\rm{,}}\,\,BC = 6\;\;{\rm{cm}}.\) Gọi \(K\) là trung điểm của đoạn thẳng \(AC\). Độ dài \(BK\) là
\(3\;\;{\rm{cm}}\).
\(4,5\;\;{\rm{cm}}\).
\(7,5\;\;{\rm{cm}}\).
\(10\;\;{\rm{cm}}\).
Tổng số đo các góc trong tứ giác bằng
\(90^\circ \).
\(120^\circ \).
\(180^\circ \).
\(360^\circ \).
Cho hai đa thức:
\(A = {x^2}y + 5xy - 1\) và \(B = 3y\left( {3y - x} \right) + \left( { - 2{x^2}{y^2} - 6x{y^3} + 4xy} \right):\frac{2}{3}xy\).
a)Đa thức \(A\)có bậc là 2.
b) Đa thức \(B\)không chia hết cho 6.
c) Với \(x = \frac{1}{2};\)\(y = 4\) thì \(B = - 6\).
d) Tổng của hai đa thức \(A\) và \(B\) có hạng tử tự do là 6.
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m}}{\rm{,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm}}{\rm{,}}\)chiều cao \(90{\rm{ cm}}\)(như hình vẽ).
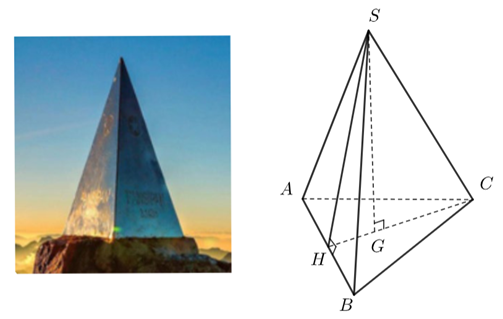
a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.
b) Độ dài cạnh \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).
c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).
d) Diện tích xung quanh của hình chóp \(S.ABC\) là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
Kết quả của phép chia \(\left( {5{x^5}{y^4}z + \frac{1}{2}{x^4}{y^2}{z^3} - 2x{y^3}{z^2}} \right):\frac{1}{4}x{y^2}z\) là đa thức bậc mấy?
Tìm giá trị của \(x\) thỏa mãn\[{x^3} + 9{x^2} + 27x + 19 = 0\].
Một khối bê tông có dạng như hình vẽ bên. Phần đáy của bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh 40 cm, chiều cao 25 m. Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao 100 cm. Tính thể tích của khối bê tông đó (làm tròn kết quả đến hàng đơn vị với đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{3}}}).\]
![Một khối bê tông có dạng như hình vẽ bên. Phần đáy của bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh 40 cm, chiều cao 25 m. Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao 100 cm. Tính thể tích của khối bê tông đó (làm tròn kết quả đến hàng đơn vị với đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{3}}}).\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid9-1750320212.png)
Tìm \(x\) trong hình vẽ bên dưới (đơn vị: độ). 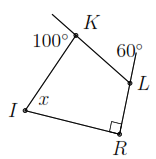
Cho biểu thức \(A = \frac{4}{{{x^2} + x + 1}}\) và \(B = \frac{2}{{1 - x}} + \frac{{2{x^2} + 4x}}{{{x^3} - 1}}\) với \(x \ne 1.\)
a) Tính giá trị của biểu thức \(A\) khi \(x = - 2.\)
b) Tìm biểu thức \(C\) biết \(A = B + C\).
c) Chứng minh giá trị của biểu thức \(C\) luôn nhận giá trị dương với mọi \(x \ne 0,x \ne 1.\)
1. Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\]đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\]Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\)(xem hình vẽ).Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\]có “an toàn” không?![Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid0-1750320479.png)
2.Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao \(21{\rm{ m}}{\rm{,}}\) độ dài cạnh đáy là \(34{\rm{ m}}\).
![Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không? (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid1-1750320488.png)
Tính tổng diện tích của các tấm kính để phủ kín bốn mặt bên của bảo tàng này (các kết quả làm tròn đến hàng đơn vị).
Đa thức nào sau đây chưa thu gọn?
\[4{x^2} + x - y\];
\[{x^4}y + x - 2y{x^4}\];
\[ - {x^3}y + \frac{2}{5}{y^2}\];
\[\frac{{x + 2y}}{5}\].
Tích của hai đơn thức \(\frac{1}{2}x{y^3}\) và \(x\left( { - 8y} \right)x{z^2}\) có phần hệ số là
\(\frac{1}{2}\);
\( - 8\);
\( - 4\);
\(7\).
Biết \(M + 5{x^2} - 2xy = 6{x^2} + 10xy - {y^2}\). Đa thức \(M\) là
\(M = {x^2} + 12xy - {y^2}\);
\(M = {x^2} - 12xy - {y^2}\);
\(M = {x^2} - 12xy + {y^2}\);
\(M = - {x^2} - 12xy + {y^2}\).
Các đơn thức điền vào ô trống trong khai triển lần lượt là
\(3b\) và \(3{b^3}\);
\(b\) và \(3{b^3}\);
\(3b\) và \(27{b^3}\);
\(3b\) và \(9{b^2}\).
Kết quả của biểu thức \({\left( {x - 5} \right)^2} - {\left( {x + 5} \right)^2}\) là
\( - 20x\)
\(50\)
\(20x\);
\(2{x^2} + 50\).
Phân tích đa thức \({x^3} - 2{x^2} + x\) thành nhân tử ta được
\(x{\left( {x - 1} \right)^2}\);
\({x^2}\left( {x - 1} \right)\);
\(x\left( {{x^2} - 1} \right)\);
\(x{\left( {x + 1} \right)^2}\).
Đâu là tính chất đúng của phân thức đại số?
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\);
\(\frac{A}{B} = \frac{{A \cdot M}}{B}\,\,\left( {B,M \ne 0} \right)\);
\(\frac{A}{B} = \frac{A}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\);
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot N}}\,\,\left( {B,M,N \ne 0,N \ne M} \right)\).
Thực hiện phép tính \(\frac{{x - 1}}{{x - y}} + \frac{{1 - y}}{{y - x}}\) ta được kết quả là
\(0\);
\(\frac{{x - y + 2}}{{x - y}}\);
\(\frac{{x + y - 2}}{{x - y}}\);
\(1\).
Hình chóp tứ giác đều có bao nhiêu đường trung đoạn?
\(1\);
\(2\);
\(3\);
\(4\).
Hình chóp tam giác đều và hình chóp tứ giác đều có chung đặc điểm nào sau đây?
Đáy là tam giác đều;
Đáy là hình vuông;
Các cạnh bên bằng nhau;
Mặt bên là các tam giác đều.
Cho tam giác \(ABC\) có đường cao \(AH.\) Biết \(AC = 15\;\;{\rm{cm}},\,\,AH = 12\;\;{\rm{cm}}{\rm{,}}\,\,BH = 9\;\;{\rm{cm}}.\) Hỏi tam giác \(ABC\) là tam giác gì?
Tam giác vuông;
Tam giác cân;
Tam giác đều;
Tam giác tù.
Các góc của tứ giác có thể là
4 góc nhọn;
4 góc tù;
2 góc vuông, 1 góc nhọn và 1 góc tù;
1 góc vuông và 3 góc nhọn.
Thu gọn biểu thức:
a) \(\left( {30{x^4}{y^3} - 25{x^2}{y^3} - 3{x^4}{y^4}} \right):5{x^2}{y^3};\) b) \({x^3}{y^4}\left( {{x^2} - 2{y^3}} \right) - 2{x^3}{y^3}\left( {{x^4} - {y^4}} \right).\)
Phân tích đa thức thành nhân tử:
a) \(5{x^2}\left( {x - y} \right) - 15xy\left( {y - x} \right)\); b) \({\left( {x + y} \right)^2} - 6\left( {x + y} \right) + 9\); c) \({x^2} - 5x + 6\).
Cho \[P = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} + \frac{{2x + 1}}{{1 - {x^3}}}\] với \(x \ne 1.\)
a) Rút gọn biểu thức \(P.\)
b) Tính giá trị của biểu thức \(P\) tại \(x = 2.\)
c) Chứng minh \(P > 0\) với \(x > 0,\,x \ne 1.\)
Vẽ, cắt và gấp mảnh bìa như đã chỉ ra ở hình bên dưới để được hình chóp tứ giác đều.
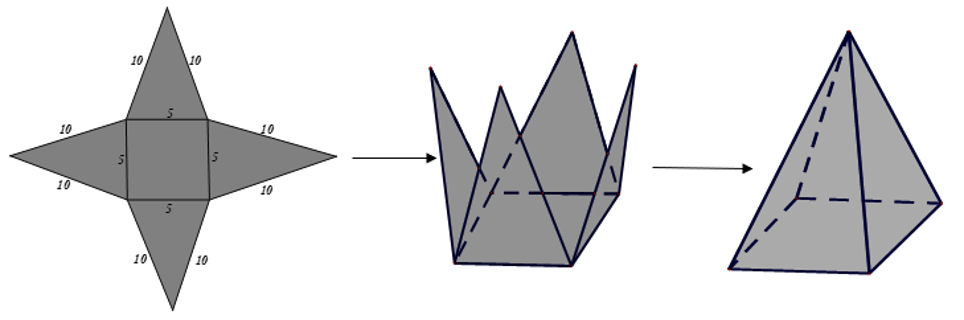
a) Trong hình chóp tứ giác đều trên có bao nhiêu tam giác cân bằng nhau?
b) Tính diện tích tất cả các mặt của hình chóp tứ giác đều này. Biết độ dài trung đoạn của hình chóp tứ giác đều là 9,68 cm.
a) Tìm \(x\) trong hình vẽ bên.b) Một công ty muốn làm một đường ống dẫn từ nhà máy \(C\) trên bờ biển đến một điểm \(B\) trên đất liền. Điểm \(A\) trên đảo cách điểm \(B\) là \(9\,\;{\rm{km}}.\) Giá để xây dựng đường ống từ nhà máy (điểm \(C)\) đến điểm \(B\) trên đất liền là \(5\,\,000\,\,{\rm{USD}}/{\rm{km}}.\) Khoảng cách từ \(A\) đến \(C\) là \(12\;\,{\rm{km}}{\rm{.}}\) Em hãy tính chi phí làm đường ống từ điểm \(C\) tới điểm \(B\) của công ty trên bằng tiền VNĐ (kết quả làm tròn đến hàng nghìn). Biết \(1\,\,{\rm{USD}} = 24\,\,300\) VNĐ tại thời điểm đó.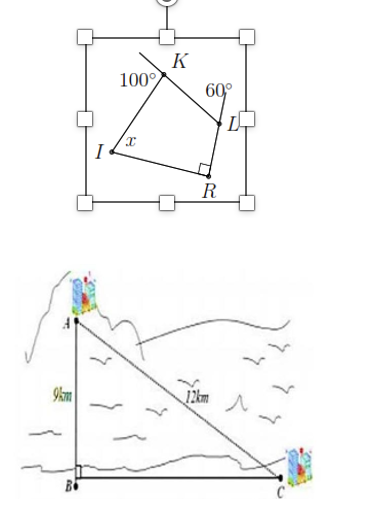
Cho \(x,y,z\) là ba số thỏa mãn điều kiện:
\[2{x^2} + {y^2} + {z^2} - 2xy - 2xz + yz - 3y - 5z + 17 = 0.\]
Tính giá trị của biểu thức \(S = {\left( {x - 4} \right)^{2023}} + {\left( {y - 4} \right)^{2025}} + {\left( {z - 4} \right)^{2027}}.\)








