Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án - Đề 3
38 câu hỏi
Biểu thức nào không phảilà đa thức trong các biểu thức sau?
\(2{x^2}y + 3 + xy\).
\(\frac{{x + y}}{2}\).
\(2 - \frac{{x + 1}}{{x - 1}}\).
\(x\left( {x + 2y} \right)\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3{x^2}y\)?
\(3{x^2}yz\).
\(\frac{1}{2}xyx\).
\(x{y^2}\).
\( - 3{x^2}z\).
Bậc của đa thức \({x^2}{y^5} - {x^2}{y^4} + {y^6} + 1\) là
\[4\].
\(5\).
\(6\).
\(7\).
Hệ số của \[{x^4}\] trong đa thức \[A = \left( {{x^3} - 2{x^2} + x - 1} \right)\left( {5{x^3} - x} \right)\]là
\[4\].
\[ - 4\].
\[ - 6\].
\[6\].
Hằng đẳng thức bình phương của một hiệu là
\[{\left( {A + B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B - {B^2}\].
Khai triển của \({x^3} - 27\) là
\(\left( {x - 3} \right)\left( {{x^2} - 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 6x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} - 6x + 9} \right)\).
Đâu là tính chất đúng của phân thức đại số?
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
\(\frac{A}{B} = \frac{{A \cdot M}}{B}\,\,\left( {B,M \ne 0} \right)\).
\(\frac{A}{B} = \frac{A}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot N}}\,\,\left( {B,M \ne 0,N \ne M} \right)\).
Phân thức \(\frac{{ - x - y}}{3}\) bằng với phân thức nào sau đây?
\(\frac{{x - y}}{{ - 3}}\).
\(\frac{{x + y}}{3}\).
\(\frac{{x - y}}{3}\).
\(\frac{{x + y}}{{ - 3}}\).
Cho các miếng bìa sau:
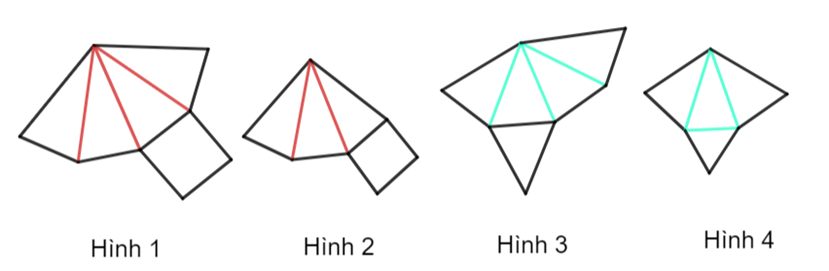
Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Diện tích xung quanh của hình chóp \(S.ABCD\) (hình bên) gồm diện tích những mặt nào?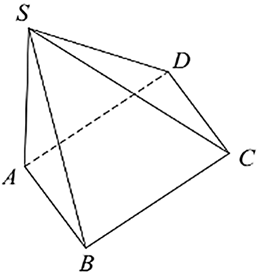
Mặt \(SBC,\,\,ABCD,\,\,SAB\).
Mặt \(SAB,\,\,SBC,\,\,SCD,\,\,SDA\).
Mặt \(SAB,\,\,SAD,\,\,SBC,\,\,ABCD\).
Mặt \(ABCD.\)
Một cây cao \[12\,\,{\rm{m}}\]mọc cạnh bờ sông. Trên đỉnh cây có một con chim đang đậu và chuẩn bị sà xuống bắt con cá trên mặt nước (như Hình 1 và được mô phỏng như Hình 2). Hỏi con chim sẽ bay một đoạn ngắn nhất bằng bao nhiêu mét thì bắt được con cá? (Biết con cá cách gốc cây \[5\,\,{\rm{m}}\] và nước cao mấp mé bờ sông). 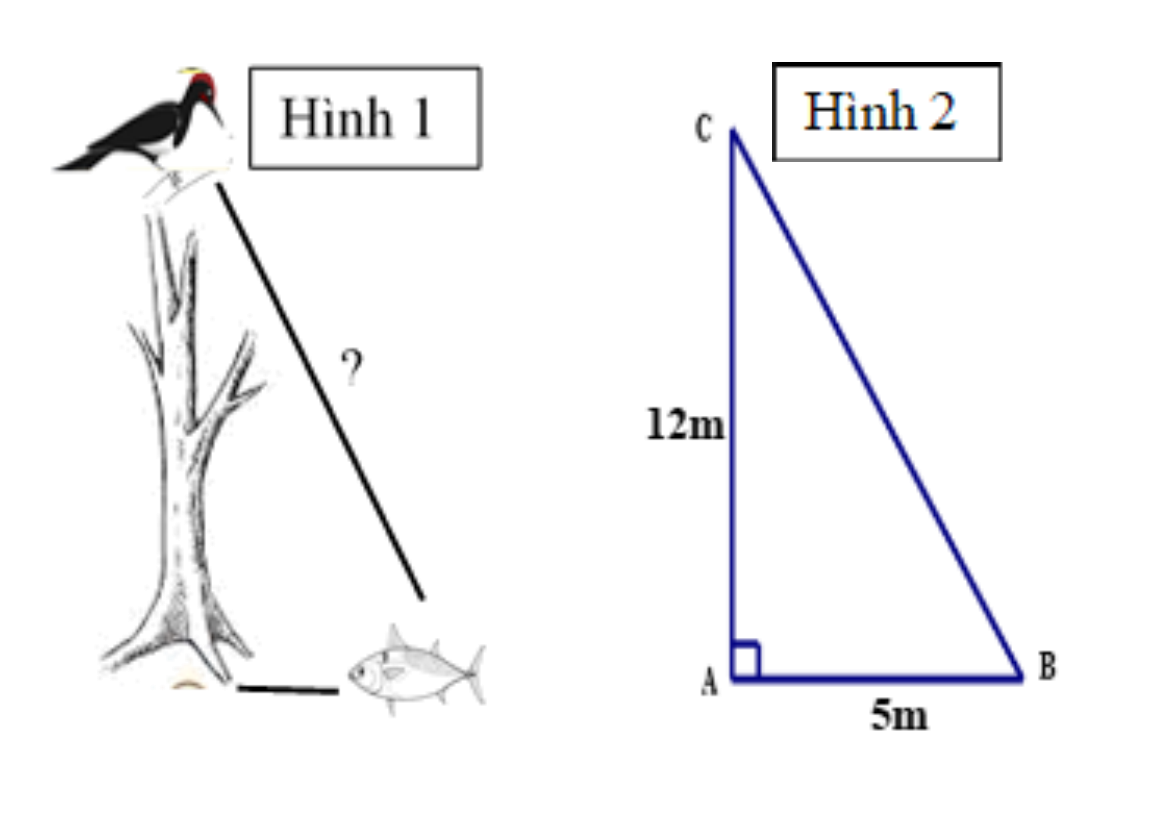
\(12\;\;{\rm{cm}}\).
\(13\,\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
\(AB\) và \(BC\) là hai cạnh kề nhau.
\(BC\) và \(AD\) là hai cạnh đối nhau.
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau.
\(AC\) và \(BD\) là hai đường chéo.
Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5{x^3}{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy.\)
a) Biểu thức \(A\) là đơn thức bậc 3.
b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)
c) Đa thức \(B\) có hai hạng tử.
d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)
Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2 m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn tất cả các mặt của hộp gỗ. Cứ mỗi mét vuông sơn cần trả \[30\,\,000\] đồng (tiền sơn và tiền công).
a) Diện tích mặt đáy hộp gỗ là \(4\,\,{{\rm{m}}^{\rm{2}}}\).
b) Diện tích xung quanh của khối gỗ là \(24\,\,{{\rm{m}}^{\rm{2}}}\).
c) Diện tích cần sơn là\(16{\rm{ }}{{\rm{m}}^2}\).
d) Chi phí bác Khôi cần phải trả là \(420\,\,000\) đồng.
![Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2 m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn tất cả các mặt của hộp gỗ. Cứ mỗi mét vuông sơn cần trả \[30\,\,000\] đồng (tiền sơn và tiền công). a) Diện tích mặt đáy hộp gỗ là \(4\,\,{{\rm{m}}^{\rm{2}}}\). b) Diện tích xung quanh của khối gỗ là \(24\,\,{{\rm{m}}^{\rm{2}}}\). c) Diện tích cần sơn là \(16{\rm{ }}{{\rm{m}}^2}\). d) Chi phí bác Khôi cần phải trả là \(420\,\,000\) đồng. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid3-1750319090.png)
Cho đa thức \(A = - \frac{1}{3}x{y^2} + \frac{1}{2}{x^2}y + x{y^2} - \frac{3}{4}{x^2}y.\) Tính giá trị của \(A\) tại \(x = - 2;y = 3\).
Có bao nhiêu giá trị \(x\) thỏa mãn \[12{x^3}--27x = 0\]?
Cho hình hộp chữ nhật có các kích thước như hình vẽ.
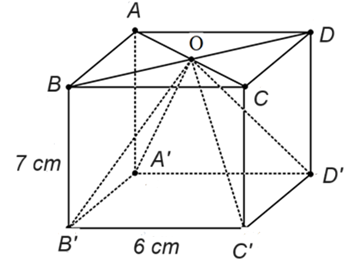
Tính thể tích hình chóp tam giác đều\(O.A'B'C'D'\) (đơn vị: \({\rm{c}}{{\rm{m}}^{\rm{3}}}).\)
Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\].
![Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\]. Tính số đo \[\widehat {{C_1}}\] (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid5-1750319289.png)
Tính số đo \[\widehat {{C_1}}\] (đơn vị: độ).
Cho \[P = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} + \frac{{2x + 1}}{{1 - {x^3}}}\] với \(x \ne 1.\)
a) Rút gọn biểu thức \(P.\)
b) Tính giá trị của biểu thức \(P\) tại \(x = 2.\)
c) Chứng minh \(P > 0\) với \(x > 0\,;\,\,x \ne 1.\)
1.Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\]\[(A\]là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\]nếu \[BC = 5\,\,{\rm{cm}}\]thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao? 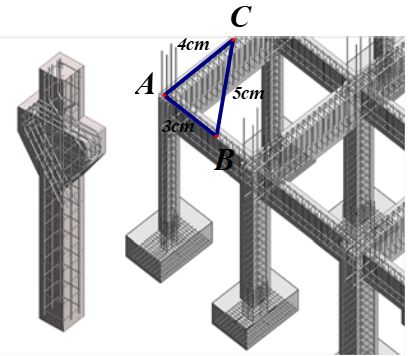
2. Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm}}{\rm{,}}\) chiều cao \({\rm{2}}{\rm{,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\)
![1. Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\] \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid6-1750319356.png)
Biểu thức nào sau đây là đa thức?
\[\frac{{x + 2y}}{3}\];
\[x + \frac{1}{y}\];
\[ - x + \frac{2}{x}y - 3{y^2}\];
\[\frac{1}{{2x}} + {y^2}\].
Cặp đơn thức nào dưới đây là hai đơn thức đồng dạng?
\(12{x^4}{y^4}\) và \(12{x^4}{y^6}\);
\( - 12{x^4}{y^4}\) và \(12{x^6}{y^6}\);
\(12{x^6}{y^4}\) và \( - 2{x^6}{y^4}\);
\(12{x^4}{y^6}\) và \(12{x^6}{y^6}\).
Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức nào dưới đây?
\(3{x^4}\);
\( - 3{x^4}\);
\( - 2{x^3}y\);
\(2x{y^3}\).
Kết quả của phép nhân \(\left( {{x^2} - 2x + 1} \right)\left( {x - 1} \right)\) là
\({x^3} - 3{x^2} + 3x - 1\);
\({x^3} + 3{x^2} + 3x - 1\);
\({x^3} - 3{x^2} + 3x + 1\);
\({x^3} + 3{x^2} + 3x + 1\).
Kết quả của biểu thức \({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4\) là
\({x^2} + 16\);
\({x^2} + 8x + 16\);
\({x^2} - 4x\);
\({x^2}\).
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
\(7xy\left( {2x - 3y + 4xy} \right)\);
\(xy\left( {14x - 21y + 28xy} \right)\);
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\);
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
Biểu thức nào sau đây không phải là phân thức đại số?
\(\frac{1}{x}\);
\(x\);
\(\frac{0}{x}\);
\(\frac{x}{0}\).
Phân thức nào sau đây không phải là phân thức đối của phân thức \(\frac{{1 - x}}{x}\)?
\(\frac{{x + 1}}{x}\);
\(\frac{{ - \left( {1 - x} \right)}}{x}\);
\( - \frac{{1 - x}}{x}\);
\(\frac{{x - 1}}{x}\).
Đặc điểm nào sau đây là sai đối với hình chóp tam giác đều \(S.ABC?\)
Đáy \(ABC\) là tam giác đều;
\(SA = SB = SC\);
Tam giác \(SBC\) là tam giác đều;
\(\Delta SAB = \Delta SBC = \Delta SCA\).
Diện tích xung quanh của hình chóp \(S.ABCD\) (hình bên) gồm diện tích những mặt nào?
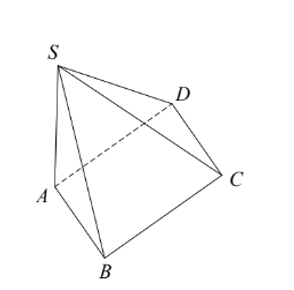
Mặt \(SBC,\,\,ABCD,\,\,SAB\);
Mặt \(SAB,SBC,SCD,SDA\);
Mặt \(SAB,SAD,SBC,ABCD\);
Mặt \(ABCD\).
Cho tam giác \(ABC\) vuông có cạnh huyền \(AB = \sqrt {117} \;\;{\rm{cm}}\) và cạnh góc vuông \(BC = 6\;\;{\rm{cm}}.\) Gọi \(K\) là trung điểm của đoạn thẳng \(AC\). Độ dài \(BK\) là
\(3\;\;{\rm{cm}}\);
\(4,5\;\;{\rm{cm}}\);
\(7,5\;\;{\rm{cm}}\);
\(10\;\;{\rm{cm}}\).
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
\(AB\) và \(BC\) là hai cạnh kề nhau;
\(BC\) và \(AD\) là hai cạnh đối nhau;
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau;
\(AC\) và \(BD\) là hai đường chéo.
Thu gọn biểu thức:
a) \(\left( { - 9{x^2}{y^3} + 6{x^3}{y^2} - 4x{y^2}} \right):3x{y^2};\) b) \(\frac{1}{2}xy\left( {{x^5} - {y^3}} \right) - {x^2}y\left( {\frac{1}{4}{x^4} - {y^3}} \right).\)
Phân tích đa thức thành nhân tử:
a) \[3x\left( {3 - x} \right) - 6\left( {x - 3} \right)\]; b) \({\left( {{x^2} + 1} \right)^2} - 4{x^2}\); c) \[{x^6} + {x^3} - {x^2} - 1\].
Cho \(A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}\) với \(x \ne \pm 2.\)
a) Rút gọn biểu thức \(A.\)
b) Tính giá trị của \(A\) khi \(x = 4.\)
c) Tìm giá trị nguyên của \(x\) để \(A\) nhận giá trị nguyên dương.
Hình ảnh bên là ảnh của một lọ nước hoa hình kim tự tháp. Khi đậy nắp, lọ có dạng hình chóp tứ giác đều (tính cả thân lọ và nắp lọ) trong đó nắp lọ cũng là hình chóp tứ giác đều có chiều cao 5 cm, cạnh đáy 2,5 cm. Chiều cao thân lọ và cạnh đáy lọ đều bằng chiều cao của nắp lọ. Bỏ qua độ dày của vỏ.
a) Tính thể tích của lọ nước hoa hình kim tự tháp đó.
b) Tính dung tích của lọ nước hoa đó ra đơn vị mi – li – lít (làm tròn kết quả đến hàng đơn vị).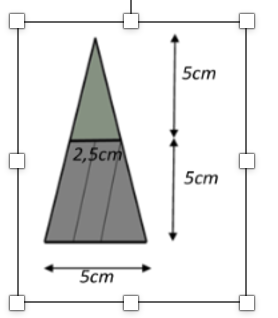
Một hồ bơi có dạng tứ giác \(ABCD\) được mô tả như hình vẽ bên. Biết \(AC\) là tia phân giác \(\widehat {BAD}\) và \(\widehat {DAC} = 40^\circ \).
a) Tính \(\widehat {BCD}.\)
b) Biết \(AB = 7,66\) m và \(BC = 6,43\) m. Một vận động viên bơi lội muốn bơi từ \(A\) đến \(C\) trong 20 giây thì cần bơi với vận tốc là bao nhiêu (làm tròn kết quả đến hàng phần mười)?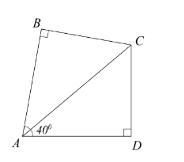
Cho \(x,y\) thỏa mãn \({x^2} + 2xy + 6x + 6y + 2{y^2} + 8 = 0.\) Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \(P = x + y + 2024.\)








