Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án - Đề 2
38 câu hỏi
Đa thức nào sau đây chưa thu gọn?
\[4{x^2} + x - y\].
\[{x^4}y + x - 2y{x^4}\].
\[ - {x^3}y + \frac{2}{5}{y^2}\].
\[\frac{{x + 2y}}{5}\].
Bậc của biểu thức \(A = 2{x^2}y \cdot 5x{y^3}\) là
\(5\).
\(6\).
\(7\).
\(8\).
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\).
Đơn thức \(B\) và đơn thức \(C\).
Đơn thức \(A\) và đơn thức \(B\).
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Cho biểu thức \(H = \left( {2x - 3} \right)\left( {x + 7} \right) - 2x\left( {x + 5} \right) - x\). Khẳng định nào sau đây là đúng?
\(H = 21 - x\).
\(H > 0\).
\(H < - 1\).
\(10 < H < 20\).
Đẳng thức nào sau đây là hằng đẳng thức?
\({x^2} - x = - x + {x^2}\).
\(x\left( {x - 1} \right) = x - {x^2}\).
\({\left( {a - b} \right)^2} = - {\left( {b - a} \right)^2}\).
\(a - 2 = 2 - a\).
Kết quả phân tích đa thức \(6{x^2}y - 12x{y^2}\) là
\(6xy\left( {x + y} \right)\).
\(6xy\left( {x - y} \right)\).
\(6xy\left( {x + 2y} \right)\).
\(6xy\left( {x - 2y} \right)\).
Phân thức \(\frac{A}{B} = \frac{C}{D}\,\,\left( {A,\,\,B \ne 0} \right)\) khi
\(AB = CD\).
\(AD = BC\).
\(\frac{A}{D} = \frac{C}{B}\).
\(\frac{A}{D} = \frac{B}{C}\).
Phân thức \(\frac{{1 - x}}{{y - x}}\) bằng với phân thức nào sau đây?
\(\frac{{x - 1}}{{y - x}}\).
\(\frac{{1 - x}}{{x - y}}\).
\(\frac{{x - 1}}{{x - y}}\).
\(\frac{{y - x}}{{1 - x}}\).
Khẳng định nào sau đây là đúng?
Hình chóp tam giác đều có 3 mặt.
Hình chóp tứ giác đều có 4 đỉnh.
Hình chóp tứ giác đều có đáy là hình thoi.
Hình chóp tam giác đều có 6 cạnh.
Một hình chóp tứ giác đều có cạnh đáy là \(a\) và độ dài trung đoạn là \(b\) thì có diện tích xung quanh là
\({S_{xq}} = 2ab.\)
\({S_{xq}} = ab.\)
\({S_{xq}} = \frac{1}{2}ab.\)
\({S_{xq}} = 4ab.\)
Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AH.\)Biết \(AH = 4\;\;{\rm{cm}},\,\,AB = 5\;\;{\rm{cm}}.\) Chu vi tam giác \(ABC\) bằng
\(16\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
\(12\;\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
Đường chéo của tứ giác lồi \(ABCD\)là 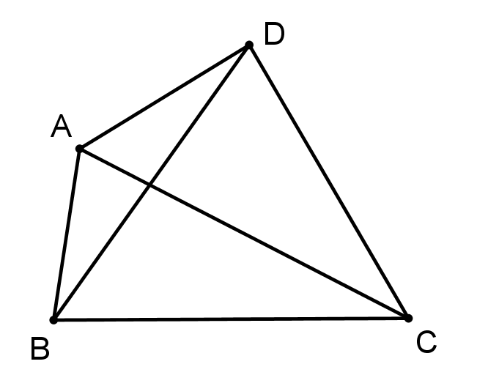
\[AB,\,\,CD\].
\[BC,\,\,CD\].
\(AC,\,\,BD\).
\(AC,\,\,CD\).
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn \(B = A + M\,;\, & P = \left( {x - 3} \right)M - y - \left( {x + y} \right)\left( {xy - 3y} \right).\)
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Hình vẽ dưới đây mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng \[1{\rm{ m}}\,;\] phần trên có dạng hình chóp tứ giác đều với chiều cao bằng \[0,6\,\,{\rm{m}}.\] Biết rằng \(1{\rm{ }}{{\rm{m}}^3}\) bê tông mác 200 cần khoảng \[350,55\,\,{\rm{kg}}\] xi măng và \[185\,\,l\] nước.
a) Thể tích phần trên (có dạng hình chóp tứ giác đều) của khối bê tông là\(0,2{\rm{ c}}{{\rm{m}}^3}.\)![Hình vẽ dưới đây mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng \[1{\rm{ m}}\,;\] phần trên có dạng hình chóp tứ giác đều với chiều cao bằng \[0,6\,\,{\rm{m}}.\] Biết rằng \(1{\rm{ }}{{\rm{m}}^3}\) bê tông mác 200 cần khoảng \[350,55\,\,{\rm{kg}}\] xi măng và \[185\,\,l\] nước. a) Thể tích phần trên (có dạng hình chóp tứ giác đều) của khối bê tông là \(0,2{\rm{ c}}{{\rm{m}}^3}.\) b) Thể tích của khối bê tông là \(1,2{\rm{ c}}{{\rm{m}}^3}.\) c) Khối lượng xi măng cần dùng để làm khối bê tông đó là \[0,5\] tấn. d) Lượng nước cần dùng để làm khối bê tông đó là \(0,185{\rm{ }}{{\rm{m}}^3}.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid0-1750305801.png)
b) Thể tích của khối bê tông là \(1,2{\rm{ c}}{{\rm{m}}^3}.\)
c) Khối lượng xi măng cần dùng để làm khối bê tông đó là\[0,5\] tấn.
d) Lượng nước cần dùng để làm khối bê tông đó là\(0,185{\rm{ }}{{\rm{m}}^3}.\)
Xác định phần hệ số của tích của hai đơn thức \(\frac{1}{2}x{y^3}\) và \(x\left( { - 8y} \right)x{z^2}\).
Giá trị của biểu thức \[A = {\left( {3x + 1} \right)^2} + {\left( {3x--1} \right)^2}--2\left( {3x--1} \right)\left( {3x + 1} \right)\] bằng bao nhiêu?
Cho hình chóp tứ giác đều có thể tích bằng \({\rm{50}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\) chiều cao là \({\rm{6}}\;{\rm{cm}}{\rm{.}}\) Độ dài cạnh đáy của hình chóp đó(đơn vị:\({\rm{cm}}\)).
Cho tứ giác \[ABCD\] có \(\widehat A = 50^\circ \,;\,\,\widehat B = 130^\circ \,;\,\,\widehat C = 80^\circ \). Tính số đo của \(\widehat D\) (đơn vị: độ).
![Cho tứ giác \[ABCD\] có \(\widehat A = 50^\circ \,;\,\,\widehat B = 130^\circ \,;\,\,\widehat C = 80^\circ \). Tính số đo của \(\widehat D\) (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid1-1750305887.png)
1. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị)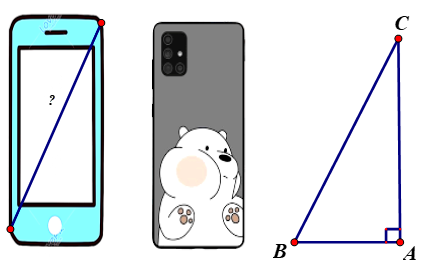
2. Một chiếc lều ở trại hè cho học sinh có dạng hình chóp tứ giác đều với chiều cao bằng \[2,8\,\,{\rm{m}};\] độ dài cạnh đáy bằng \[3\,{\rm{m}}\,{\rm{.}}\]
a) Tính thể tích không khí bên trong của chiếc lều.
b) Người ta muốn sơn phủ bên ngoài cả bốn mặt xung quanh của lều và không sơn phủ phần làm cửa có diện tích là\[5\,\,{{\rm{m}}^2}.\] Biết độ dài trung đoạn của lều là \[3,18\,\,{\rm{m}}\]và cứ mỗi mét vuông sơn cần trả \[35\,\,000\] đồng. Tính số tiền cần phải trả để hoàn thành việc sơn phủ cho lều.
![1. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị) 2. Một chiếc lều ở trại hè cho học sinh có dạng hình chóp tứ giác đều với chiều cao bằng \[2,8\,\,{\rm{m}};\] độ dài cạnh đáy bằng \[3\,{\rm{m}}\,{\rm{.}}\] a) Tính thể tích không khí bên trong của chiếc lều. b) Người ta muốn sơn phủ bên ngoài cả bốn mặt xung quanh của lều và không sơn phủ phần làm cửa có diện tích là \[5\,\,{{\rm{m}}^2}.\] Biết độ dài trung đoạn của lều là \[3,18\,\,{\rm{m}}\] và cứ mỗi mét vuông sơn cần trả \[35\,\,000\] đồng. Tính số tiền cần phải trả để hoàn thành việc sơn phủ cho lều. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid2-1750305977.png)
Cho biểu thức \(A = \frac{4}{{{x^2} + x + 1}}\) và \(B = \frac{2}{{1 - x}} + \frac{{2{x^2} + 4x}}{{{x^3} - 1}}\) với \(x \ne 1.\)
a) Tính giá trị của biểu thức \(A\) khi \(x = - 2.\)
b) Tìm biểu thức \(C\) biết \(A = B + C\).
c) Chứng minh giá trị của biểu thức \(C\) luôn nhận giá trị dương với mọi \(x \ne 0,x \ne 1.\)
Biểu thức nào sau đây là đơn thức?
\[\left( {1 + x} \right){x^3}\];
\[x + 2y\];
\(\left( {xy + z} \right)t\);
\(3x{y^2}{z^5}\).
Bậc của đa thức \(M = {x^8} + {x^2}{y^7} - {y^5} + x\) là
\(1\);
\(5\);
\(8\);
\(9\).
Giá trị của đa thức \[2{x^2}y + 3x{y^2} - 2y{x^2} - 2{y^2}x + 3\] tại \(x = \frac{{ - 2}}{3};\,\,y = \frac{1}{2}\) là
\[\frac{{ - 17}}{6}\];
\[\frac{{17}}{6}\];
\[\frac{{ - 19}}{6}\];
\[\frac{{19}}{6}\].
Đẳng thức nào sau đây là hằng đẳng thức?
\[{x^2} - {x^3} = {x^3} - {x^2}\];
\(x\left( {x - 1} \right) = x - {x^2}\);
\({\left( {a - b} \right)^2} = {\left( {b - a} \right)^2}\);
\(a - 2 = 2 - a\).
Điền vào chỗ trống sau:
\(2\);
\(4\);
\(8\);
\(16\).
Biết \({x^3} + 125 = A.B\) và \(A\) là đa thức có bậc bằng 1. Khi đó biểu thức \(B\) là
\({x^2} - 5x + 25\);
\({x^2} + 5x + 25\);
\({x^2} - 10x + 25\);
\({x^2} + 10x + 25\).
Phân thức \(\frac{A}{B} = \frac{C}{D}\,\,\left( {B,\,\,D \ne 0} \right)\) khi
\(AB = CD\);
\(AD = BC\);
\(\frac{A}{D} = \frac{C}{B}\);
\(\frac{A}{D} = \frac{B}{C}\).
Kết quả nào sau đây là sai?
\(\frac{{4{x^2} - 5z}}{{3xy}} + \frac{{4{x^2} + 5z}}{{3xy}} = \frac{{8x}}{{3y}}\);
\(\frac{{x + 3}}{{x - y}} + \frac{x}{{y - x}} - \frac{{x - 3}}{{x - y}} = \frac{{ - x + 6}}{{x - y}}\);
\[\frac{{3{a^2} - 5ab}}{{{a^2} - {b^2}}} + \frac{{2{a^2} - 4{b^2}}}{{{b^2} - {a^2}}} + \frac{{7ab - 3{b^2}}}{{{a^2} - {b^2}}} = \frac{{5a + 7b}}{{a + b}}\];
\(\frac{3}{{x + 3}} - \frac{{x - 6}}{{{x^2} + 3x}} = \frac{2}{x}\).
Hình chóp tam giác đều không có đặc điểm nào sau đây?
Có các cạnh bên bằng nhau;
Có đáy là hình vuông;
Có các mặt bên là các tam giác cân;
Có chân đường vuông góc của đỉnh là tâm đường tròn ngoại tiếp tam giác đáy.
Cho hình vẽ bên, trung đoạn của hình chóp tứ giác \(S.MNPQ\) là
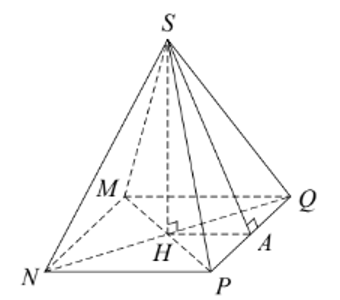
\(SH\);
\(SA\);
\(HA\);
\(NQ\) hoặc \(MP\).
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau?
\(15\;\;{\rm{cm}};\,\,8\;\;{\rm{cm;}}\,\,{\rm{18}}\;\;{\rm{cm}}\);
\[21\;\;{\rm{dm}};\,\,20\;\;{\rm{dm;}}\,\,29\;\;{\rm{dm}}\];
\(5\;\;{\rm{m}};\,\,6\;\;{\rm{m;}}\,\,{\rm{8}}\;\;{\rm{m}}\);
\(2\;\;{\rm{cm}};\,\,3\;\;{\rm{cm;}}\,\,4\;\;{\rm{cm}}\).
Cho hình vẽ bên.
Khẳng định nào sau đây là khẳng định sai?
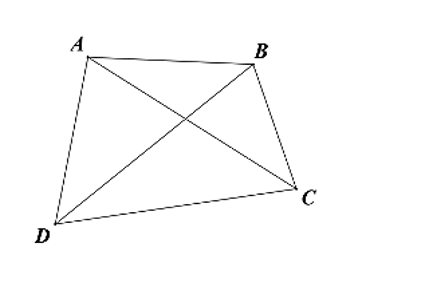
Hai đỉnh kề với đỉnh \(A\) là \(B\) và \(D\);
Hai đỉnh đối nhau là \(A\) và \(C;\) \(B\) và \(D\);
Tứ giác \(ABCD\) có 2 đường chéo;
Các cạnh của tứ giác là \(AB,\,\,BC,\)\(CD,\,\,DA,\) \(AC,\) \(BD\).
Thu gọn biểu thức:
a) \(\left( {4{x^4} - 8{x^2}{y^2} + 12{x^5}y} \right):\left( { - 4{x^2}} \right);\) b) \({x^2}\left( {x - {y^2}} \right) - xy\left( {1 - xy} \right) - {x^3}.\)
Phân tích đa thức thành nhân tử:
a) \[10{x^2}\left( {2x - y} \right) + 6xy\left( {y - 2x} \right);\] b) \({x^2} - 2x + 1 - {y^2}\); c) \[{x^2} - 8x + 12\].
Cho biểu thức \(A = \frac{{x + 15}}{{{x^2} - 9}} + \frac{2}{{x + 3}}\)với \(x \ne \pm 3\).
a) Rút gọn biểu thức \(A\).
b) Tìm \(x\) để \(A\) có giá trị bằng \(\frac{{ - 1}}{2}\).
c) Tìm số tự nhiên \[x\] để \(A\) có giá trị nguyên.
Kim tự tháp là một công trình kiến trúc tuyệt đẹp bằng kính tọa lạc ngay lối vào của bảo tàng Louvre, Pari. Kim tự tháp có dạng là hình chóp tứ giác đều với chiều cao 21 m và độ dài cạnh đáy là 34 m. Các mặt bên của kim tự tháp là các tam giác đều (xem hình ảnh minh họa bên).

a) Tính thể tích của kim tự tháp Louvre.
b) Hỏi nếu sử dụng loại gạch hình vuông có cạnh là 60 cm để lót sàn thì cần bao nhiêu viên gạch? Biết diện tích của các đường rãnh giữa các viên gạch lót sàn là 156 m2.
a) Cho tứ giác \(ABCD\) có \(\widehat {C\,} = 60^\circ ,\widehat {D\,} = 80^\circ ,\widehat {A\,\,} - \widehat {B\,} = 10^\circ .\) Tính số đo của \(\widehat {A\,\,}.\)
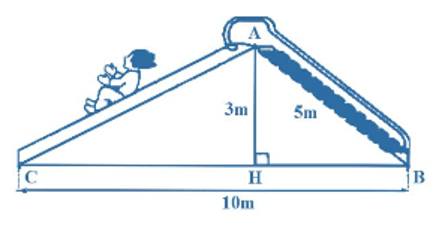
b) Tính chiều dài đường trượt \(AC\) trong hình vẽ bên (kết quả làm tròn hàng phần mười).
Cho các số \(x,y\) thỏa mãn đẳng thức: \(5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0.\) Tính giá trị của biểu thức \(M = {\left( {x + y} \right)^{2023}} + {\left( {x - 2} \right)^{2024}} + {\left( {y + 1} \right)^{2025}}\).








