Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án - Đề 1
38 câu hỏi
Đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) (với \(a,\,\,b\) là hằng số) có hệ số là
\[ - 36{a^2}{b^2}\].
\[ - 36\].
\[36{a^2}{b^2}\].
\[ - 36{a^2}\].
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3{x^2}y\)?
\(3{x^2}yz\).
\(\frac{1}{2}xyx\).
\(x{y^2}\).
\( - 3{x^2}z\).
Tích của đa thức \[6xy\]và đa thức \[2{x^2} - 3y\]là đa thức
\[12{x^2}y + 18x{y^2}\].
\[12{x^3}y - 18x{y^2}\].
\[12{x^3}y + 18x{y^2}\].
\[12{x^2}y - 18x{y^2}\].
Điều kiện của số tự nhiên \(n\)để phép chia \(\left( {4{x^{10}}y - x{y^7} + {x^5}{y^4}} \right):2{x^n}{y^n}\)là phép chia hết là
\(n = 0\).
\(n = 1\).
\(n = 5\).
\(n \in \left\{ {0\,;\,\,1} \right\}\).
Hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) có tên là
bình phương của một tổng.
bình phương của một hiệu.
tổng hai bình phương.
hiệu hai bình phương.
Kết quả của khai triển phép tính \({\left( {\frac{1}{2}x - 1} \right)^2}\) là
\(\frac{1}{2}{x^2} - \frac{1}{2}x + 1\).
\(\frac{1}{4}{x^2} - 1\).
\(\frac{1}{4}{x^2} - \frac{1}{2}x + 1\).
\(\frac{1}{4}{x^2} - x + 1\).
Phân thức\(\frac{A}{B}\) xác định khi nào?
\(B < 0\).
\(B = 0\).
\(B \ne 0\).
\(B > 0\).
Phân thức nào sau đây bằng với phân thức \(\frac{y}{{3x}}\) (với giả thiết các phân thức đều có nghĩa)?
\(\frac{{3{y^2}}}{{9x{y^2}}}\).
\(\frac{{{y^2}}}{{9x{y^2}}}\).
\(\frac{{3{y^2}}}{{9xy}}\).
\(\frac{{3y}}{{9x{y^2}}}\).
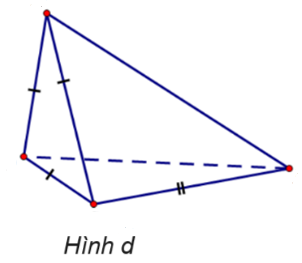
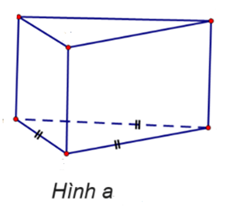
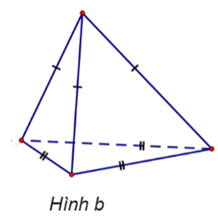
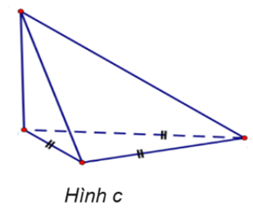
Cho các hình vẽ sau:
 |  |  |
|
Trong những hình dưới đây, những hình nào là hình chóp tam giác đều?
Hình a.
Hình b.
Hình c.
Hình d.
Thể tích của hình chóp tam giác đều bằng
diện tích đáy nhân với chiều cao.
\(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(\frac{1}{2}\) chiều cao nhân với diện tích đáy.
\(\frac{3}{2}\) diện tích đáy nhân với chiều cao.
Độ dài cạnh \(BC\) trong \(\Delta ABC\) cân tại \(A\) ở hình vẽ bên là 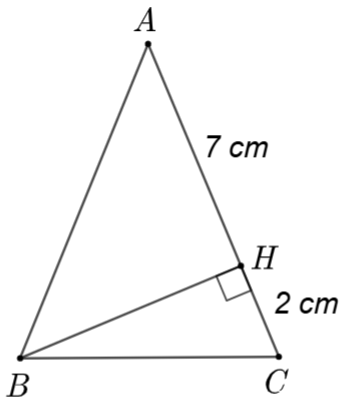
\(4\;\;{\rm{cm}}\).
\(5\;\;{\rm{cm}}\).
\(6\;\;{\rm{cm}}\).
\(7\;\;{\rm{cm}}\).
Trong các khẳng định sau, khẳng định nào đúng?
Tứ giác có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 3 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 4 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 1 đường chéo, 4 đỉnh và 4 góc.
Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5{x^3}{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy.\)
a) Biểu thức \(A\) là đơn thức bậc 3.
b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)
c) Đa thức \(B\) có hai hạng tử.
d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)
Bạn Uyên dự định làm 4 hộp quà có dạng hình chóp tứ giác đều như hình bên có cạnh đáy \(6{\rm{ cm}}{\rm{,}}\) chiều cao của mặt bên xuất phát từ đỉnh là \(4{\rm{ cm}}{\rm{.}}\)
a) Mỗi hộp quà có 5 mặt.
b) Diện tích xung quanh của một hộp quà là\(48{\rm{ c}}{{\rm{m}}^2}\).
c) Diện tích các mặt của hộp quà là\(60{\rm{ c}}{{\rm{m}}^2}\).
d) Diện tích giấy mà bạn Uyên cần dùng để làm 4 hộp quà \(240{\rm{ c}}{{\rm{m}}^2}.\)
Cho \(B - \left( {5{x^2} - 2xyz} \right) = 2{x^2} + 2xyz + 1\). Hạng tử tự do của đa thức \(B\) là bao nhiêu?
Cho biểu thức \[{x^3} - 9{x^2} + 27x - m\] là lập phương của một tổng. Tính giá trị của\(m.\)
Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
![Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid4-1750305079.png)
Cho tứ giác \(MNPQ\) có \(\widehat N = \widehat M + 10^\circ ,\)\(\widehat P = \widehat N + 10^\circ ,\)\(\widehat Q = \widehat P + 10^\circ .\)Tính số đo của \(\widehat M\) của tứ giác \(MNPQ\) (đơn vị: độ).
Cho biểu thức \(A = \frac{{{x^2}}}{{{x^2} - 4}} - \frac{x}{{x - 2}} - \frac{2}{{x + 2}}.\)
a) Viết điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A\).
c) Tìm giá trị của \(x\) để \(A = 2.\)
1. Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
![1. Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid5-1750305147.png)
2. Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là \[20{\rm{ cm}}.\]
a) Tính độ dài trung đoạn của hình chóp.
b) Tính diện tích xung quanh của chiếc đèn.
c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là \[1{\rm{ m}}\] là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí \(A)\) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?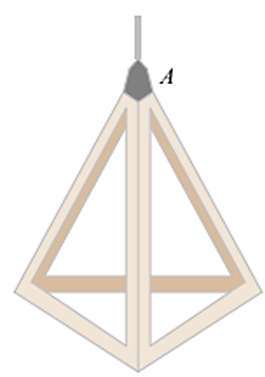
Trong các biểu thức sau, biểu thức nào là đơn thức?
\(\frac{1}{x} + y\);
\( - \frac{{{x^2}z}}{5}\);
\(\left( {2 - x} \right){y^2}\);
\(\sqrt {xyz} \).
Đa thức nào sau đây không phải là đa thức bậc 4?
\(4x{y^2}z\);
\({x^4} - {3^5}\);
\(x{y^2} + xyzt\);
\({x^4} - \frac{1}{2}x{y^3}z\).
Cho đa thức \(A = - \frac{1}{3}x{y^2} + \frac{1}{2}{x^2}y + x{y^2} - \frac{3}{4}{x^2}y.\) Giá trị của \(A\) tại \(x = - 2;y = 3\) là
\(A = - \frac{{15}}{{13}}\);
\(A = - 12\);
\(A = - 15\);
\(A = 14\).
Khẳng định nào sau đây là đúng?
\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) = {x^3} + {\left( {2y} \right)^3}\);
\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) = {x^3} - {\left( {4y} \right)^3}\);
\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) = {x^3} + {\left( {4y} \right)^3}\);
\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) = {x^3} - {\left( {2y} \right)^3}\).
Điền vào chỗ trống sau:
\(2x\);
\(4x\);
\(2\);
\(4\).
Kết quả phân tích đa thức \(6{x^2}y - 12x{y^2}\) là
\(6xy\left( {x - 2y} \right)\);
\(6xy\left( {x - y} \right)\);
\(6xy\left( {x + 2y} \right)\);
\(6xy\left( {x + y} \right)\).
Phân thức \(\frac{A}{B}\) xác định khi nào?
\(B < 0\);
\(B = 0\);
\(B \ne 0\);
\(B > 0\).
Ta không nên quy đồng cho bài toán nào dưới đây?
\(\frac{1}{{x - 1}} - \frac{x}{{1 - x}}\);
\(\frac{2}{{x - y}} - \frac{3}{{x + y}}\);
\(x - \frac{1}{{x + y}}\);
\(\frac{1}{{a - 1}} + \frac{1}{{{a^2} - 1}}\).
Hình chóp tứ giác đều có mặt bên là hình gì?
Tam giác cân;
Tam giác đều;
Hình chữ nhật;
Hình vuông.
Cho hình chóp tam giác đều \(A.BCD\) như hình vẽ bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp?
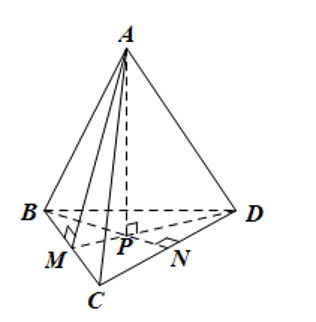
\(AC\);
\(AM\);
\(BN\);
\(AP\).
Độ dài cạnh \(BC\) trong \(\Delta ABC\) cân tại \(A\) ở hình vẽ bên là
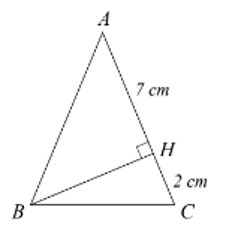
\(4\;\;{\rm{cm}}\);
\(5\;\;{\rm{cm}}\);
\(6\;\;{\rm{cm}}\);
\(7\;\;{\rm{cm}}\).
Tổng số đo các góc trong tứ giác bằng
\(90^\circ \);
\(120^\circ \);
\(180^\circ \);
\(360^\circ \).
Thu gọn biểu thức:
a) \(\left( { - 12{x^{13}}{y^{15}} + 6{x^{10}}{y^{14}}} \right):\left( { - 3{x^{10}}{y^{14}}} \right);\) b) \[\left( {x - y} \right)\left( {{x^2} - 2x + y} \right) - {x^3} + {x^2}y.\]
Phân tích đa thức thành nhân tử:
a) \[xy + {y^2}--x--y;\] b) \({\left( {{x^2}{y^2} - 8} \right)^2} - 1;\) c) \[{x^2}--7x--8.\]
Cho biểu thức \(A = \frac{{{x^2}}}{{{x^2} - 4}} - \frac{x}{{x - 2}} - \frac{2}{{x + 2}}.\)
a) Viết điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A\).
c) Tìm giá trị của \(x\) để \(A = 2.\)
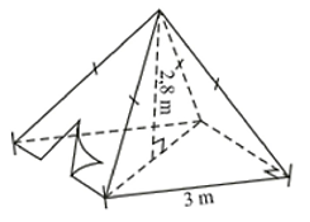
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như hình bên.
a) Tính thể tích không khí bên trong chiếc lều.
b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\;\;{\rm{m}}\) và giá vải là \(15\,\,000\) đồng/m2. Ngoài ra, nếu mua vải với hóa đơn trên \(20\) m2 thì được giảm giá \(5\% \) trên tổng hóa đơn.
Một chiếc diều được mô tả như hình vẽ bên.
a) Tính số đo góc \(D\) ở đuôi chiếc diều biết các góc ở đỉnh \(\widehat {A\,\,} = \widehat {B\,} = \widehat {C\,} = 102^\circ .\)
b) Tính độ dài khung gỗ đường chéo \(BD\) biết \(OD = 26,7\;\;{\rm{cm}}\) (làm tròn kết quả đến hàng phần mười).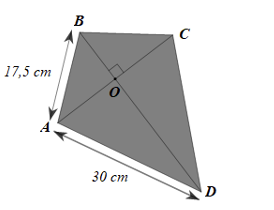
Tìm giá trị nhỏ nhất của biểu thức \(M = {x^2} - 2x\left( {y + 1} \right) + 3{y^2} + 2025.\)