Bộ 10 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 3
38 câu hỏi
Cho góc lượng giác \(\left( {Oa,Ob} \right)\) có số đo là \(50^\circ .\) Hỏi số đo của góc lượng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là \(Oa\) và tia cuối là \(Ob?\)
\({\alpha _1} = 140^\circ .\)
\({\alpha _2} = 410^\circ .\)
\({\alpha _3} = 320^\circ .\)
\({\alpha _4} = 230^\circ .\)
Đổi số đo của góc \(\alpha = \frac{\pi }{3}\) sang độ.
\(\alpha = 90^\circ .\)
\(\alpha = 30^\circ .\)
\(\alpha = 60^\circ .\)
\(\alpha = 45^\circ .\)
Chọn khẳng định đúng.
\(\sin \left( {x + y} \right) = \sin x\cos y + \cos x\sin y\).
\(\cos \left( {x - y} \right) = \cos x\cos y - \sin x\sin y\).
\(\cos \left( {x + y} \right) = \cos x\cos y + \sin x\sin y\).
\(\sin \left( {x - y} \right) = \sin x\cos y + \cos x\sin y\).
Khẳng định nào dưới đây sai?
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\cos 2a = 2\cos a - 1\).
\(\sin 2a = 2\sin a\cos a\).
\(\cos 2a = {\cos ^2}a - {\sin ^2}a\).
Mệnh đề nào dưới đây là sai?
Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \[y = \tan x\] tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi .\)
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
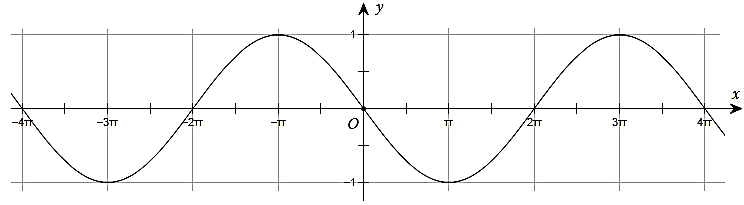
Hỏi hàm số đó là hàm số nào?
\(y = \sin \frac{x}{2}.\)
\(y = \cos \frac{x}{2}.\)
\(y = - \cos \frac{x}{4}.\)
\(y = \sin \left( { - \frac{x}{2}} \right).\)
Trong các hàm số sau, hàm số nào là hàm số chẵn?
\(y = \sin x.\)
\(y = \cos x.\)
\(y = \tan x.\)
\(y = \cot x.\)
Hai phương trình được gọi là tương đương khi
chúng có cùng số nghiệm.
chúng có cùng tập nghiệm.
chúng cùng có nghiệm.
chúng cùng có duy nhất một nghiệm.
Nghiệm của phương trình: \(1 + \tan x = 0\).
\(x = \frac{\pi }{4} + k\pi \,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{4} + k\pi \,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Phương trình \[\sin x = \frac{1}{2}\] có nghiệm thỏa mãn \[\frac{{ - \pi }}{2} \le x \le \frac{\pi }{2}\] là
\[x = \frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}\].
\[x = \frac{\pi }{6}\].
\[x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\].
\[x = \frac{\pi }{3}\].
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{a{n^2}}}{{n + 1}}\) (\(a\) là hằng số), \({u_{n + 1}}\) là số hạng nào sau đây?
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 2}}\).
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 1}}\).
\({u_{n + 1}} = \frac{{a.{n^2} + 1}}{{n + 1}}\).
\({u_{n + 1}} = \frac{{a{n^2}}}{{n + 2}}\).
Cho dãy số \[\left( {{u_n}} \right)\] với \[{u_n} = \frac{n}{{{3^n} - 1}}\]. Ba số hạng đầu tiên của dãy số lần lượt là
\[\frac{1}{2};\frac{1}{4};\frac{3}{{27}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{26}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{25}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{28}}\].
Khẳng định nào sau đây là sai?
Dãy số \( - \frac{1}{2};\,0;\,\frac{1}{2};\,1;\frac{3}{2};.....\) là một cấp số cộng: \(\left\{ \begin{array}{l}{u_1} = - \frac{1}{2}\\d = \frac{1}{2}\end{array} \right.\).
Dãy số \(\frac{1}{2};\,\frac{1}{{{2^2}}};\,\frac{1}{{{2^3}}};.....\) là một cấp số cộng:\(\left\{ \begin{array}{l}{u_1} = \frac{1}{2}\\d = \frac{1}{2}\end{array} \right.\).
Dãy số :\[\;--{\rm{ }}2;{\rm{ }}--{\rm{ }}2;{\rm{ }}--{\rm{ }}2;{\rm{ }}--{\rm{ }}2;{\rm{ }} \ldots \;\]là cấp số cộng \(\left\{ \begin{array}{l}{u_1} = - 2\\d = 0\end{array} \right.\).
Dãy số: \[0,1;{\rm{ }}0,01;{\rm{ }}0,001;{\rm{ }}0,0001;{\rm{ }} \ldots \]không phải là một cấp số cộng.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 5\) và \(d = 3.\) Mệnh đề nào sau đây đúng?
\({u_{15}} = 34.\)
\({u_{15}} = 45.\)
\({u_{13}} = 31.\)
\({u_{10}} = 35.\)
Cho dãy số: –1; 1; –1; 1; –1; … Khẳng định nào sau đây là đúng?
Dãy số này không phải là cấp số nhân.
Số hạng tổng quát \({u_n} = {1^n} = 1\).
Dãy số này là cấp số nhân có \({u_1} = - 1,\,q = - 1\).
Số hạng tổng quát \({u_n} = {\left( { - 1} \right)^{2n}}\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \[{u_1} = 3\] và \({u_2} = - 6\). Công bội \(q\) của cấp số nhân đó là
\[2\].
\[ - 2\].
\[ - 9\].
\[9\].
Điều tra về chiều cao của 100 học sinh lớp 11 trường THPT Nguyễn Xuân Ôn, ta được kết quả:
Chiều cao (cm) | \(\left[ {150;152} \right)\) | \(\left[ {152;154} \right)\) | \(\left[ {154;156} \right)\) | \(\left[ {156;158} \right)\) | \(\left[ {158;160} \right)\) | \(\left[ {160;162} \right)\) | \(\left[ {162;168} \right)\) |
Số học sinh | 5 | 10 | 45 | 20 | 16 | 3 | 1 |
Mẫu số liệu trên có bao nhiêu nhóm?
7.
6.
5.
8.
Cho mẫu số liệu ghép nhóm trong đó có một nhóm là \(\left[ {200;\,235} \right)\). Độ dài của nhóm này là
200.
235.
5.
35.
Khảo sát thời gian sử dụng điện thoại di động trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Thời gian sử dụng điện thoại (giờ) | \(\left[ {1;2} \right)\) | \(\left[ {2;3} \right)\) | \(\left[ {3;4} \right)\) | \(\left[ {4;\,5} \right)\) |
Số học sinh | 10 | 30 | 7 | 3 |
Mẫu số liệu này có số mốt là
0.
1.
2.
3.
Cho mẫu số liệu ghép nhóm có cỡ mẫu \(n\) như sau:

Giả sử nhóm chứa trung vị là nhóm thứ \(p\): \(\left[ {{a_p};\,{a_{p + 1}}} \right)\), \({m_p}\) là tần số nhóm \(p\). Công thức tính trung vị của mẫu số liệu ghép nhóm này là
\({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
\({M_e} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
\({M_e} = {a_p} + \frac{{\frac{{3n}}{2} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
\({M_e} = {a_p} + \frac{{\frac{n}{2} - {m_p}}}{{{m_1} + ... + {m_{p - 1}}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
Cho góc \(\alpha \) thỏa \({\rm{cot}}\alpha = \frac{3}{4}\) và \(0^\circ < \alpha < 90^\circ .\) Khẳng định nào sau đây đúng?
\[{\rm{cos}}\alpha = - \frac{4}{5}.\]
\[{\rm{cos}}\alpha = \frac{4}{5}.\]
\(\sin \alpha = \frac{4}{5}.\)
\({\rm{sin}}\alpha = - \frac{4}{5}.\)
Biến đổi biểu thức \[A = 4\sin x.\sin 2x.\sin 3x\] thành tổng.
\[A = - \sin 4x + \cos 2x - \sin 6x\].
\[A = \sin 4x - \cos 2x - \sin 6x\].
\[A = \sin 4x - \sin 2x + \sin 6x\].
\[A = \sin 4x + \sin 2x - \sin 6x\].
Cho \(\alpha ,\,\,\beta \) là hai góc nhọn thỏa mãn \(\tan \alpha = \frac{1}{7}\), \(\tan \beta = \frac{3}{4}\). Góc \(\alpha + \,\beta \) có giá trị bằng
\(\frac{\pi }{6}\).
\(\frac{\pi }{4}\).
\(\frac{\pi }{3}\).
\[\frac{\pi }{2}\].
Tìm tập giá trị \(T\) của hàm số \[y = 5 - 3\sin x.\]
\(T = \left[ { - 1;1} \right].\)
\(T = \left[ { - 3;3} \right].\)
\(T = \left[ {2;8} \right].\)
\(T = \left[ {5;8} \right].\)
Tìm tập xác định \(D\) của hàm số \[y = \frac{{\cos x}}{{\sin \left( {x - \frac{\pi }{2}} \right)}}.\]
\[D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},\,k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k\pi ,\,k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {\pi + 2k\pi ,\,k \in \mathbb{Z}} \right\}.\]
Phương trình \(m.\cos x - 1 = 0\) có nghiệm khi \(m\) thỏa mãn điều kiện
\[\left[ \begin{array}{l}m \le - 1\\m \ge 1\end{array} \right.\].
\[m \ge - 1\]
\[m \ge 1\].
\[\left\{ \begin{array}{l}m \ge - 1\\m \le 1\end{array} \right.\].
Phương trình \[3\cot x - \sqrt 3 = 0\] có nghiệm là
\[x = \frac{\pi }{6} + k\pi \],\[k \in \mathbb{Z}\].
\[x = \frac{\pi }{3} + k\pi \],\[k \in \mathbb{Z}\].
\[x = \frac{\pi }{3} + k2\pi \],\[k \in \mathbb{Z}\].
Vô nghiệm.
Trong các dãy số sau, dãy số nào không là dãy số bị chặn?
\(\left( {{a_n}} \right)\) với \({a_n} = {3^n}\).
\(\left( {{u_n}} \right)\) với \({u_n} = \sin \left( {n\frac{\pi }{2}} \right)\).
\(\left( {{b_n}} \right):2,4,6,8,10\).
\(\left( {{v_n}} \right)\) với \({v_n} = \frac{1}{{n + 1}}\).
Xét dãy số :\(1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{{16}}...\). Tìm công thức số hạng tổng quát của dãy số trên.
\({a_n} = \frac{1}{{{2^n}}}\).
\({b_n} = \frac{1}{{{2^{n - 1}}}}\).
\({c_n} = - \frac{1}{2}n + \frac{3}{2}\).
\({d_n} = \frac{1}{8}{n^2} - \frac{7}{8}n + \frac{7}{4}\).
Cho dãy số \(\left( {{u_n}} \right)\) có: \[{u_1} = - 3;d = \frac{1}{2}\]. Khẳng định nào sau đây là đúng?
\[{u_n} = - 3 + \frac{1}{2}\left( {n + 1} \right)\].
\[{u_n} = - 3 + \frac{1}{2}n - 1\].
\[{u_n} = - 3 + \frac{1}{2}\left( {n - 1} \right)\].
\[{u_n} = n\left( { - 3 + \frac{1}{4}\left( {n - 1} \right)} \right)\].
Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?
\(1635.\)
\(1792\).
\(2055\).
\(3125\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) yà \(q = 2\). Tống \(n\) số hạng đầu tiên của cấp số nhân đã cho bằng \( - 1533\). Tìm \(n.\)
\(n = 9\).
\(n = 10\).
\(n = 11\).
\(n = 12\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có các số hạng khác không, tìm \({u_1}\) biết: \(\left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} = 15}\\{u_1^2 + u_2^2 + u_3^2 + u_4^2 = 85}\end{array}} \right.\).
\({u_1} = 1,{u_1} = 2\).
\({u_1} = 1,{u_1} = 8\).
\({u_1} = 1,{u_1} = 5\).
\({u_1} = 1,{u_1} = 9.\)
Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Mốt của mẫu số liệu ghép nhóm này là
\({M_o} = 131,02\).
\({M_o} = 130,23\).
\({M_o} = 129,02\).
\({M_o} = 132,04\).
Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của \(30\) củ khoai từ như sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là
\({Q_1} = 85,5\).
\({Q_1} = 87,5\).
\({Q_1} = 86,5\).
\({Q_1} = 86,75\).
III. Hướng dẫn giải tự luận
(1 điểm) Giải các phương trình lượng giác sau:
a) \({\sin ^2}x + 5\sin x\cos x + 6{\cos ^2}x = 6\).
b) \(\cos 3x - \sin 2x - \cos x = 0\).
(1 điểm) Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 29 + 3{\rm{sin}}\frac{\pi }{{12}}\left( {t - 9} \right)\)với \(h\) tính bằng độ \({\rm{C}}\) và \(t\) là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ \({\rm{C}}\) và vào lúc mấy giờ?
(1 điểm)Biết rằng tồn tại đúng ba giá trị \({m_1},\,{m_2},\,{m_3}\) của tham số \(m\) để phương trình \({x^3} - 9{x^2} + 23x + {m^3} - 4{m^2} + m - 9 = 0\) có ba nghiệm phân biệt lập thành một cấp số cộng. Tính giá trị của biểu thức \(P = m_1^3 + m_2^3 + m_3^3\).








