Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 9
28 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Cho mệnh đề: “Nếu \[a + b < 2\] thì một trong hai số \[a\] hoặc \[b\] nhỏ hơn 1”. Mệnh đề có thể được phát biểu lại bằng cách nào sau đây?
“Điều kiện đủ để một trong hai số a hoặc b nhỏ hơn 1 là \(a + b < 2\)”;
“Điều kiện đủ để \[a + b < 2\] là một trong hai số \[a\] hoặc \[b\] nhỏ hơn 1”;
“Điều kiện cần và đủ để \(a + b < 2\) là một trong hai số a hoặc b nhỏ hơn 1”;
“Điều kiện cần và đủ để một trong hai số \[a\] hoặc \[b\] nhỏ hơn 1 là \[a + b < 2\]”.
Cho mệnh đề .Tìm mệnh đề phủ định của mệnh đề \(P\).
;
;
;
.
Cho các mệnh đề sau đây:
\[\left( I \right):\] Nếu tam giác \(ABC\) đều thì \(AB = AC.\)
\[\left( {II} \right):\] Nếu \(a + b\) là số chẵn thì \(a\) và \(b\) là các số chẵn.
\[\left( {III} \right):\] Nếu tam giác \(ABC\) có tổng hai góc bằng \(90^\circ \) thì tam giác \(ABC\) vuông cân.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
0.
3.
2.
\(1\).
Phát biểu nào sau đây là mệnh đề?
Dịch covid thật khủng khiếp!;
Số \(3\) là số may mắn của tôi;
Trái Đất là một hành tinh trong hệ mặt trời;
Hố đen vũ trụ thật bí ẩn.
Tập hợp \[A = \left\{ {x \in \mathbb{R}\left| { - 2 \le x < 11} \right.} \right\}\] bằng tập hợp nào dưới đây?
\[A = \left[ { - 2\,;\,11} \right)\];
\[A = \left[ { - 2\,;\,10} \right]\];
\[A = \left\{ { - 2; - 1;0;1;2;3;4;5;6;7;8;9;10} \right\}\];
\[A = \left( { - 2\,;\,11} \right]\].
Cho \(x\) là một phần tử của tập hợp \(A\). Cách viết nào sau đây là đúng?
\(x \subset A\);
\(\left\{ x \right\} \in A\);
\(x \in A\);
\(A \subset \left\{ x \right\}\).
Cho hai tập hợp \(M = \left\{ {x \in \mathbb{Z},\left| {x - 1} \right| - 5 \le 1} \right\}\). Có bao nhiêu số nguyên thuộc tập hợp \(M\)?
\(8\);
\(14\);
Vô số;
\(7\).
Gọi \(M\) là giá trị lớn nhất và \(m\) là giá trị nhỏ nhất của biểu thức \(F\left( {x;\,y} \right) = 4x - 3y\) trên miền nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \ge 3\\x - y \le 5\\y \le 5\end{array} \right.\) được biểu diễn bởi hình vẽ sau:
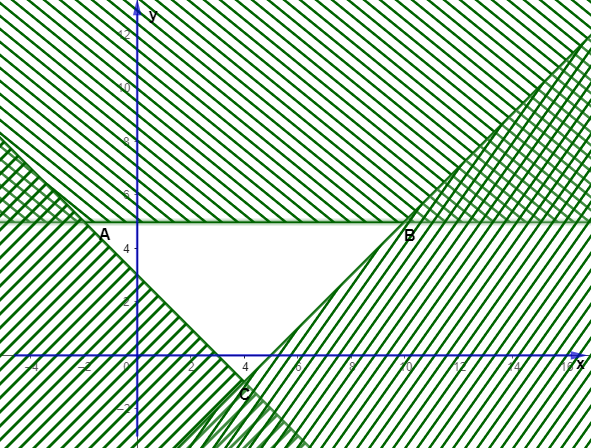
Giá trị \(M - m\) bằng
\(2\);
\(4\);
\(48\);
\(25\).
Cho \(A\) và \(B\) là hai tập hợp khác rỗng. Phát biểu nào dưới đây là sai?
\(\left( {A \cap B} \right) \subset B\);
\(\left( {A\backslash B} \right) \subset B\);
\(B \subset \left( {A \cup B} \right)\)
\(\left( {B\backslash A} \right) \subset B\).
Bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(x - {12^2}y > 7\);
\(3x + 4{y^2} \le 7\);
\(\frac{2}{x} - 7y > 90\)
\(xy \ge - 9\).
Trong các hình dưới đây, hình nào biểu diễn miền nghiệm của bất phương trình \(\frac{1}{2}x - 3y \ge - 3\)?
A. 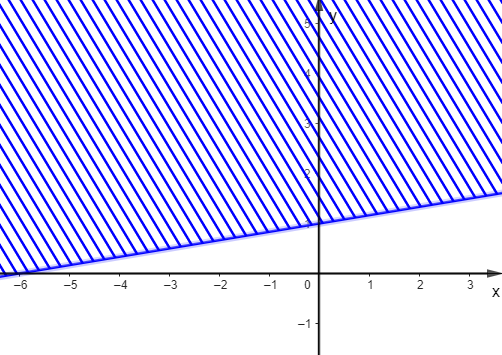 ;
;
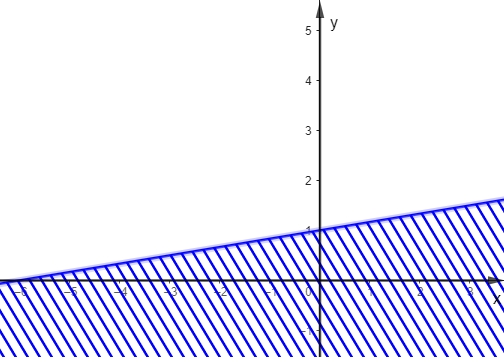
C. 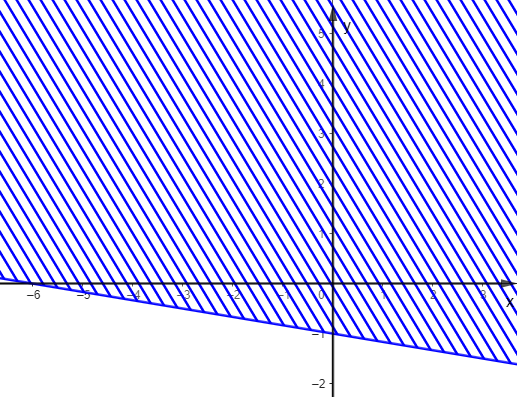 ;
;
D. 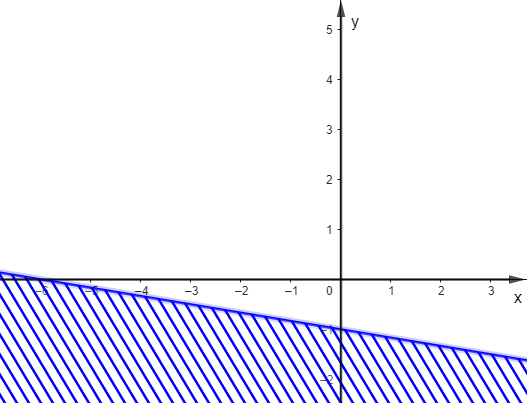 .
.
Cho bất phương trình bậc nhất hai ẩn: \(3mx - y < m + 1\). Với giá trị nào của tham số \(m\) thỏa mãn cặp \(\left( {0;\,\, - 2} \right)\) là nghiệm của bất phương trình đã cho?
\(m = \frac{5}{4}\);
\(m = - \frac{1}{2}\);
\(m = 2\frac{1}{4}\);
\(m = 1\).
Cho tập hợp \(A = \left( { - m + 2;\,\,3} \right]\) và \(B = \left[ {m;m + 5} \right]\). Giá trị của \(m\) để \(A \cap B = \emptyset \) là
\(m \ge 3\);
\(\left[ \begin{array}{l}m > 3\\m \le - \frac{3}{2}\end{array} \right.\);
\(\left[ \begin{array}{l}m < 3\\m \ge - \frac{3}{2}\end{array} \right.\);
\(m < - \frac{3}{2}\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < 1\\x + 2y \ge 0\end{array} \right.\) có miền nghiệm được biểu diễn như hình vẽ:
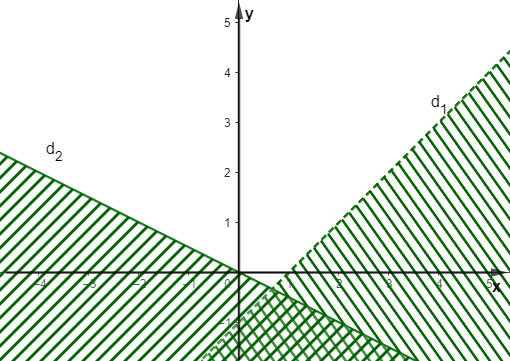
Câu nào mô tả đúng nhất miền nghiệm của hệ bất phương trình trên?
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ không kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ kể đường thẳng \({d_1}\) và không kể đường thẳng \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ không kể đường thẳng \({d_1}\) và kể cả đường thẳng \({d_2}\).
Trong các cặp số: \(\left( {0;\,\,0} \right);\,\,\,\left( { - 1;\,\,1} \right);\,\,\left( { - 2;\,\,3} \right)\,;\,\,\left( {4;\,\,1} \right)\) có bao nhiêu cặp số là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y \le 1\\2x - y > - 2\end{array} \right.\)?
\(1\);
\(2\);
\(3\);
\(4\).
Cho biết \(\cot \alpha = \frac{1}{2}\). Giá trị của \(P = \frac{{2\sin \alpha - 2\cos \alpha }}{{2\cos \alpha + 3\sin \alpha }}\) bằng bao nhiêu?
\(P = 0\);
\(P = \frac{1}{4}\);
\(P = - \frac{1}{4}\);
\(P = \frac{2}{7}\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y < 0\\y \ge 0\\x \ge - 1\end{array} \right.\). Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) là điểm thỏa mãn miền nghiệm của hệ bất phương trình trên. Khi đó biểu thức nào dưới đây là đúng?
\({x_0} + {y_0} \ge 0\);
\({x_0} < 0\);
\({y_0} \ge - 1\);
\({x_0} - {y_0} > - 1\).
Cho \(0^\circ \le \alpha ,\beta \le 180^\circ \) thỏa mãn \(\alpha + \beta = 90^\circ \). Đẳng thức nào dưới đây đúng?
\(\tan \alpha = {\rm{cos}}\beta \);
\[{\rm{cos}}\alpha = - {\rm{sin}}\beta \];
\(\sin \alpha = - \sin \beta \);
\(\cot \alpha = \tan \beta \).
Giá trị của biểu thức \(M = \tan \left( { - 10^\circ } \right).\tan 20^\circ ...\tan \left( { - 70^\circ } \right).\tan 80^\circ \) bằng
\(M = - 1\);
\(M = 1\);
\(M = 0\);
\(M = - 4\).
Cho \(0^\circ < \alpha < 90^\circ \) thỏa mãn đẳng thức \[\sin \alpha + \cos \alpha = \sqrt 2 \]. Giá trị của \(\tan \alpha + \cot \alpha \) là
\(1\);
\( - 2\);
\(0\);
\(2\).
Cho tam giác \(ABC\) có cạnh \(AB = 2cm,\widehat {ABC} = 110^\circ ,\widehat {BAC} = 35^\circ \). Độ dài cạnh \(AC\) nằm trong khoảng nào sau đây?
\(\left( {1;\,\,3} \right)\);
\(\left( {3;\,\,5} \right)\);
\(\left( {5;\,\,7} \right)\);
\(\left( {7;\,\,9} \right)\).
Cho tam giác \(ABC\) vuông tại \(A\). Nhận xét nào dưới đây là sai?
\(\sin \left( {B + C} \right) = \sin A\);
\(\sin B = {\rm{cos}}C\);
\(\tan B = \cot C\);
\(\sin \left( {\frac{{B + C}}{2}} \right) = \sin \frac{A}{2}\).
Tam giác \[ABC\] có diện tích \(S\). Nếu tăng cạnh \(BC\) lên \(2\) lần đồng thời tăng cạnh \(CA\) lên \(3\) lần và giữ nguyên độ lớn của góc \(C\) thì khi đó diện tích của tam giác mới được tạo nên bằng
\(2S\);
\(3S\);
\(4S\);
\(6S\).
Cho tam giác \(ABC\) có \(AB = 5,\,\,BC = 7,\,\,AC = 8\). Chiều cao xuất phát từ đỉnh \(A\) của tam giác \(ABC\) có độ dài là
\(\frac{{5\sqrt 3 }}{2}\);
\(10\sqrt 3 \);
\(\frac{{20\sqrt 3 }}{7}\);
\(\frac{{10\sqrt 3 }}{7}\).
Trong tam giác \(ABC\), phát biểu nào sau đây đúng?
\(\frac{{a + b + c}}{S} = r\);
\(\frac{S}{{a + b + c}} = r\);
\[\frac{S}{{2\left( {a + b + c} \right)}} = r\];
\(\frac{{2S}}{{a + b + c}} = r\).
II. PHẦN TỰ LUẬN (3 điểm)
(1,0 điểm)
a) Cho hai tập hợp \(M = \left( { - \infty ;2} \right)\) và \(N = \left[ { - 3;5} \right)\). Tìm \(M \cap N\).
b) Trong kì thi chọn học sinh giỏi cấp trường đối với hai môn Văn và Lịch sử, lớp 10 xã hội của trường THPT Núi Thành có 20 em tham gia thi (một học sinh có thể tham gia thi hai môn). Kết quả của cuộc thi là 9 em đoạt giải môn Văn, 8 em đoạt giải môn Sử và 7 em không đoạt giải môn nào. Tìm số học sinh đoạt giải cả hai môn thi đó.
(1,0 điểm)
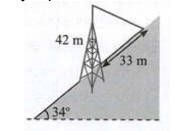
Một tháp viễn thông cao \(42\,\,m\) được dựng thẳng đứng trên một sườn dốc \(34^\circ \) so với phương ngang. Từ đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp \(33\,\,m\) (như hình vẽ). Tính chiều dài của sợi dây cáp đó.
(1,0 điểm) Một công ty cần thuê xe để chở \(120\) người và \(6,5\) tấn hàng. Nơi thuê xe có hai loại xe \(A\) và \(B\), trong đó loại xe \(A\) có \(9\) chiếc và loại xe \(B\) có \(8\) chiếc. Một chiếc xe loại \(A\) cho thuê với giá 4 triệu đồng, một chiếc xe loại \(B\) cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại \(A\) có thể chở tối đa \(20\) người và \(0,5\) tấn hàng; mỗi chiếc xe loại \(B\) có thể chở tối đa \(10\) người và \(2\) tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?








