Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 7
28 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Mệnh đề nào dưới đây là đúng?
\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\);
\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\);
\(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\);
\(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\).
Mệnh đề phủ định của mệnh đề: “số 12 chia hết cho 4 và 3” là
“Số 12 hoặc chia hết cho 4 hoặc chia hết cho 3”;
“Số 12 không chia hết cho 4 và không chia hết cho 3”;
“Số 12 không chia hết cho 4 hoặc không chia hết cho 3”;
“Số 12 không chia hết cho 4 và chia hết cho 3”.
Cho mệnh đề chứa biến . Với giá trị nào của \(a\) ta được mệnh đề sai?
\(a = - 2\);
\(a = 7\);
\(a = - 1\);
\(a = 1\).
Trong các câu sau, câu nào là mệnh đề?
“Lá cây có màu xanh rất đẹp”;
“ABCD là hình bình hành”;
“Cốm làng Vòng là ngon nhất”;
“Bắc Giang là tỉnh thuộc miền Trung Việt Nam”.
Trong các tập hợp sau, tập hợp nào là tập rỗng?
\(M = \left\{ {x \in \mathbb{N}|{x^2} - 16 = 0} \right\}\);
\(N = \left\{ {x \in \mathbb{R}|{x^2} + 2x - 5 = 0} \right\}\);
\(P = \left\{ {x \in \mathbb{Z}|{x^2} - 15 = 0} \right\}\);
\(Q = \left\{ {x \in \mathbb{Q}|{x^2} + 3x - 4 = 0} \right\}\).
Cho hai tập hợp \(M = \left\{ {x \in \mathbb{R}|2{x^2} - x = 0} \right\}\) và \(N = \left\{ {0;\,\,a} \right\}\). Với giá trị nào của \(a\) thì \(M = N\)?
\(a = 2\);
\(a = 1\);
\(a = \frac{1}{2}\);
\(a = - \frac{1}{2}\) hoặc \(a = 0\).
Cho hai tập hợp \(E = \left[ {2;\,\,4} \right]\) và \(F = \left( {0;3} \right)\). Tập hợp \(E \cup F\) bằng
\(\left( {0;\,\,4} \right]\);
\(\left[ {3;\,\,4} \right]\);
\(\left[ {2;3} \right)\);
\(\left[ {0;\,\,3} \right)\).
Cho các tập hợp sau: \(A\) = {\(x|x\) là hình bình hành}, \(B\) = {\(x|x\) là hình chữ nhật}, \(C\) = {\(x|x\) là hình thoi}, \(D\) = {\(x|x\) là hình vuông}. Mệnh đề nào sau đây sai?
\(B \cap C = D\);
\(C \cap D = D\);
\(B \cup C = D\);
\(B \cap D = D\).
Cho tập hợp \(X = \){\(x \in \mathbb{N}|x\)là ước của \(18\) và \(12\)}. Số tập con khác rỗng của tập \(X\) là
\(4\);
\(15\);
\(16\);
\(14\).
Lan muốn đống góp quà trung thu cho các cháu thiếu nhi bằng cách mua \(2\) loại kẹo từ số tiền tiết kiệm \(350\,\,000\)đồng của mình. Biết kẹo hương dâu giá \(32\,\,000\)đồng/ hộp, kẹo hương cam giá \(36\,\,000\)đồng/hộp. Lan đã mua \(x\) hộp kẹo hương dâu và \(y\)hộp kẹo hương cam. Bất phương trình nào sau đây mô tả điều kiện ràng buộc với \(x,y\)?
\(x + y \ge 35\);
\(32x + 36y \ge 350\);
\(32x + 36y \le 350\);
\(36x + 32y \le 350\).
Cặp số nào sau đây không phải là một nghiệm của bất phương trình \(x - 4y \ge 23\)?
\(\left( { - 7;\,\, - 8} \right)\);
\(\left( { - 5;\,\,6} \right)\);
\(\left( {30;\,\,1} \right)\);
\(\left( {25; - 1} \right)\).
Tập nghiệm của bất phương trình bậc nhất hai ẩn \[ax + by < c\] là
tập hợp các cặp \(\left( {x;y} \right)\) thỏa mãn điều kiện \[ax + by < c\];
tập hợp các cặp \(\left( {x;y} \right)\) thỏa mãn điều kiện \[ax + by \le c\];
tập hợp các cặp \(\left( {x;y} \right)\) thỏa mãn điều kiện \[ax + by \ge c\];
tập hợp các cặp \(\left( {x;y} \right)\) thỏa mãn điều kiện \[ax + by = c\].
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\) chứa điểm nào đưới đây?
\(\left( { - 1;4} \right)\);
\(\left( { - 11;4} \right)\);
\(\left( {0;0} \right)\);
\(\left( { - 3;4} \right)\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}3{x^2} + {y^2} < 10\\x - 2y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}{9^2}x - \sqrt y < 0\\x + 2y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}\sqrt 7 .x - y{.3^2} > 0\\x + y \le 0\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^3} + y > 0\\{x^2} - y \le 0\end{array} \right.\).
Cho biểu thức \(F\left( {x;\,\,y} \right) = x - 2y + 1\) với \(\left( {x;\,y} \right)\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l} - x - 2y \ge - 10\\2x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\). Biểu thức \(F\left( {x;\,\,y} \right)\) đạt giá trị nhỏ nhất tại cặp \(\left( {x;\,y} \right)\)có giá trị là
\(\left( {0;\,\,5} \right)\);
\(\left( {0;\,\,0} \right)\);
\(\left( {2;\,\,4} \right)\);
\(\left( {4;\,\,0} \right)\).
Cho \(\alpha \) và \(\beta \) là hai góc bù nhau, đẳng thức nào sau đây sai?
\(\cos \alpha = \cos \beta \);
\(\sin \alpha = \sin \beta \);
\(\alpha + \beta = 180^\circ \);
\(\tan \alpha = - \tan \beta \left( {\alpha ,\beta \ne 90^\circ } \right)\).
Giá trị của biểu thức \(M = {\sin ^2}37^\circ + \tan 67^\circ .\tan 23^\circ + {\rm{co}}{{\rm{s}}^2}143^\circ \) bằng
\(M = 1\);
\(M = 2\);
\(M = - 1\);
\(M = - 2\).
Giá trị \(\cot 87^\circ 6'\)gần với kết quả nào nhất sau đây?
\(19,7\);
\( - 0,05\);
\(0,1\);
\( - 19,7\).
Mệnh đề nào dưới đây là đúng?
\(\sin x + {\rm{cos}}x = 1\);
\(1 + {\sin ^2}x = \frac{1}{{{{\cot }^2}x}}\);
\({\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}\);
\[\tan x = \frac{{{\rm{cos}}\,x}}{{{\mathop{\rm s}\nolimits} {\rm{in}}\,x}}\].
Cho biết \(\tan \alpha = - \frac{1}{{\sqrt 3 }}\). Giá trị của \(P = \frac{{\sin \alpha - \cos \alpha }}{{\cos \alpha + 3\sin \alpha }}\) bằng bao nhiêu?
\(P = \sqrt 3 \);
\(P = \sqrt 3 - 1\);
\(P = \frac{{3 + 2\sqrt 3 }}{3}\);
\(P = \frac{{2\sqrt 3 - 3}}{3}\).
Cho \[\sin x + {\rm{cos}}x = m\left( { - 1 \le m \le 1} \right)\]. Tính giá trị của biểu thức \(M = \sin x\,.\,{\rm{cos}}x\).
\(M = \frac{{{m^2} + 1}}{2}\);
\(\frac{{{m^2} - 1}}{2}\);
\({m^2} - 1\);
\({m^2} + 1\).
Tam giác \(ABC\) có \(AB = 9\,\,cm,\,BC = 15\,\,cm,\,\,AC = 12\,\,cm\). Khi đó đường trung tuyến \(AM\) của tam giác \(ABC\) có độ dài là
\(10\,\,cm\);
\(9\,\,cm\);
\(7,5\,\,cm\);
\(8\,\,cm\).
Cho hình vuông \(ABCD\) có cạnh bằng \(a\). Gọi \(E\)là trung điểm cạnh \(BC\) và \(F\) là trung điểm cạnh \(AE\). Tính độ dài đoạn thẳng \(DF\).
\(DF = \frac{{a\sqrt {13} }}{4}\);
\(DF = \frac{{a\sqrt 5 }}{4}\);
\(DF = \frac{{a\sqrt 3 }}{2}\);
\(DF = \frac{{3a}}{4}\).
Công thức heron tính diện tích tam giác \(ABC\) là
\(S = pr\);
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \);
\(S = \frac{1}{2}.a.b.\sin C = \frac{1}{2}.b.c.\sin A\);
\(S = \frac{{abc}}{{4R}}\).
Cho tam giác \(ABC\) có \(AB = 2cm,\widehat {ABC} = 30^\circ ,\widehat {BAC} = 85^\circ \). Độ dài cạnh \(BC\) nằm trong khoảng nào dưới đây?
\(\left( {3;6} \right)\);
\(\left( {10;12} \right)\);
\(\left( {7;\,\,10} \right)\,\,\);
\(\left( {1;\,\,4} \right)\).
II. PHẦN TỰ LUẬN (3 điểm)
(1,0 điểm)
a) Kí hiệu \(H\) là tập hợp học sinh lớp 10A1, \(T\) là tập hợp các học sinh nam và \(G\) là tập hợp các học sinh nữ của lớp 10A1. Hãy các định các tập hợp \(T \cup G,\,\,T \cap G\) và \(H\backslash T\).
b) Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}|\left( {x + 2} \right)\left( {5{x^2} - 6x + 1} \right) = 0} \right\}\) và
\(B = \left\{ {x \in \mathbb{R}|{x^2} - \left( {2m + 1} \right)x + 2m = 0} \right\}\). Tìm điều kiện của tham số m để \(A \cup B\) có đúng 3 phần tử và tổng bình phương của chúng bằng 9.
(1,0 điểm) Sắp đến Tết, một hộ nông dân dự định trồng hoa Thược dược và hoa Cúc để bán trên diện tích 12 ha. Nếu trồng Thược dược thì cần 10 công và thu được 11 triệu đồng trên diện tích mỗi ha, nếu trồng Cúc thì cần 15 công và thu 14 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu về số tiền lớn nhất, biết rằng tổng số công không quá 150.
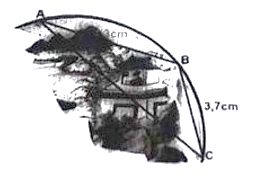
(1,0 điểm) Khi khai quật một ngôi mộ cổ người ta tìm được một mảnh của một chiếc đĩa phẳng hình tròn bị vỡ. Dựa vào các tài liệu đã có, các nhà khảo cổ đã biết hình vẽ phần còn lại của chiếc đĩa. Họ muốn làm chiếc đĩa mới phỏng theo chiếc đĩa này. Em hãy giúp họ tìm bán kính chiếc đĩa biết \(AB = 4,3\,cm;\,\,AC = 7,5\,\,cm;\,\,BC = 3,7cm\).