Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 6
28 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Cho mệnh đề \(P:\) “Nếu hai tam giác đồng dạng và có một cặp cạnh tương ứng bằng nhau thì chúng bằng nhau”. Mệnh đề đảo của mệnh đề \(P\) là
“Nếu hai tam giác bằng nhau và có một cặp cạnh tương ứng bằng nhau thì chúng đồng dạng;
“Nếu hai tam giác bằng nhau thì chúng đồng dạng và có một cặp cạnh tương ứng bằng nhau”;
“Nếu hai tam giác bằng nhau thì chúng có một cạnh tương ứng bằng nhau”;
“Hai tam giác đồng dạng và có 1 cạnh tương ứng bằng nhau khi và chỉ khi chúng bằng nhau”.
Trong các câu sau, câu không phải mệnh đề là
\(x > 3\);
Tam giác cân có một góc bằng \(45^\circ \) là tam giác vuông cân;
Trong một tam giác tổng hai cạnh lớn hơn cạnh còn lại;
\(135\) là một số nguyên tố.
Cho các câu:
“Môn xác suất thật khó!”;
“Số một nghìn tỉ là số rất lớn”;
“Phú Quốc là thành phố thuộc tỉnh Kiên Giang”;
“Việt Nam có 54 dân tộc anh em”.
Có bao nhiêu câu là mệnh đề?
\(0\);
\(1\);
\(2\);
\(3\).
Cho mệnh đề \(P \Rightarrow Q\): “Nếu tứ giác \(ABCD\) là hình thoi thì \(ABCD\)có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường”. Phát biểu mệnh đề \(P \Rightarrow Q\) bằng cách sử dụng “điều kiện cần”, “điều kiện đủ”.
“Điều kiện đủ để tứ giác \(ABCD\) là hình thoi là\(ABCD\)có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường”;
“Điều kiện cần để tứ giác \(ABCD\) là hình thoi là\(ABCD\)có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường”;
“Tứ giác \(ABCD\) là hình thoi là điều kiện cần để \(ABCD\)có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường”;
“Tứ giác \(ABCD\)có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường là điều kiện đủ để tứ giác \(ABCD\) là hình thoi”.
Cho trục số:

Phần không bị gạch trên trục số biểu diễn cho tập hợp nào?
\(\left( { - 1;\,\,7} \right)\);
\(\left[ { - 1;\,\,7} \right]\);
\(\left[ { - 1;\,\,7} \right)\);
\(\left( { - 1;\,\,7} \right]\).
Cho tập hợp \(M = \left\{ {1;\,\,3;\,\,4;\,\,a;\,\,b;\,\,d} \right\}\). Có bao nhiêu tập hợp con của \(M\) có \(4\) phần tử mà luôn chứa phần tử \(1;\,\,3;\,\,a\)?
\(1\);
\(64\);
\(3\);
\(32\).
Cho tập hợp \(H = \left\{ {x \in \mathbb{R}|{x^2} - 3x > 0} \right\}\). Tập hợp \(\mathbb{N}\backslash H\) là
\(\left[ {0;\,\,3} \right]\);
\(\left( {0;3} \right)\);
\(\left\{ {0;\,\,3} \right\}\);
\(\left\{ {0;\,\,1;\,\,2;\,\,3} \right\}\).
Cho hai tập hợp \(A,\,\,B\) như hình bên dưới:
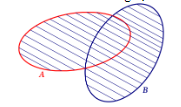
Phần gạch chéo trong hình tương ứng với tập hợp nào sau đây?
\(A \cap B\);
\({C_A}B\);
\(A \cup B\);
\(A\backslash B\).
Lớp 10A2 có \(21\) học sinh đạt học lực giỏi và \(24\) học sinh đạt hạnh kiểm tốt. Trong đó có \(15\) học sinh vừa đạt học lực giỏi và đạt hạnh kiểm tốt, \(11\) học sinh không đạt học lực giỏi và đạt hạnh kiểm tốt. Hỏi lớp 10A2 có bao nhiêu học sinh?
\(41\);
\(19\);
\(49\);
\(45\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(ax + by > c\) là:
một đường thẳng có phương trình \(ax + by = c\);
một đường tròn có phương trình \(ax + by = c\);
một nửa mặt phẳng có bờ là đường thẳng \(ax + by = c\);
một nửa mặt phẳng có bờ là đường thẳng \(d:ax + by = c\) chứa điểm \(M({x_0};\,\,{y_0})\) thỏa mãn \(a{x_0} + b{y_0} > c\)và kể cả đường thẳng d.
Cho hình vẽ bên:
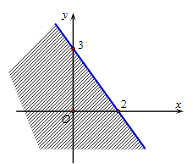
Miền nghiệm không bị gạch kể cả biên là miền nghiệm của bất phương trình có tổng hệ số \(a - b + c\) là
\( - 7\);
\( - 5\);
\(7\);
\(5\).
Cho bất phương trình bậc nhất hai ẩn: \(\left( {m - 1} \right)x - 2my \ge 9\). Tìm điều kiện của tham số \(m\) để cặp \(\left( {5;\,\, - 4} \right)\) là nghiệm của bất phương trình đã cho.
\(m \ge \frac{{14}}{{13}}\);
\(m \le - \frac{{14}}{3}\);
\(m \ge \frac{4}{{13}}\);
\(m \le - \frac{4}{3}\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}3x + {y^2} < 0\\x + 2y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y < 0\\x + 2y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} - y > 0\\x + {y^2} \le 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y > 0\\{x^2} - y \le 0\end{array} \right.\).
Biết rằng miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x - 2y \ge - 10\\2x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)có miền nghiệm là một đa giác không bị gạch chéo như hình vẽ bên dưới:
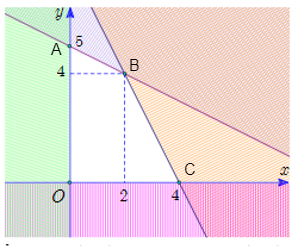
Giá trị lớn nhất của biểu thức \(F\left( {x;\,\,y} \right) = 3x - 2y + 1\) với \(\left( {x;\,y} \right)\) thỏa mãn hệ bất phương trình đã cho ở trên bằng
\(31\);
\( - 1\);
\(1\);
\(13\).
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 4y < 0\\x \ge 0\\x - y \ge - 1\end{array} \right.\)?
\(\left( {0;\,\,3} \right)\);
\(\left( {1;\,\,1} \right)\);
\(\left( { - 1;\,\,0} \right)\);
\(\left( { - 2;\,\,1} \right)\).
Trong các đẳng thức sau đây đẳng thức nào là đúng?
\(\tan 120^\circ = \sqrt 3 \);
\(\cot 120^\circ = \sqrt 3 \);
\(\cos 120^\circ = \frac{1}{2}\);
\(\sin 120^\circ = \frac{{\sqrt 3 }}{2}\).
Giá trị của biểu thức
\(M = \sin 45^\circ .\cos 135^\circ + \cos 60^\circ .\sin 150^\circ - \cos 30^\circ .\sin 120^\circ \) bằng
\(M = 1\);
\(M = 2\);
\(M = - 1\);
\(M = - 2\).
Cho góc \(\alpha \left( {0^\circ < \alpha < 180^\circ } \right)\) thỏa mãn \[{\rm{cos}}\alpha = \frac{3}{4}\]. Khi đó \[{\rm{sin}}\alpha \] bằng
\(\frac{5}{{16}}\);
\( - \frac{{\sqrt 5 }}{4}\);
\(\frac{{\sqrt 5 }}{4}\);
\( - \frac{{\sqrt 3 }}{4}\).
Cho tam giác \(ABC\). Tính \(P = \sin A.\sin \left( {B + C} \right) - \cos A.cos\left( {B + C} \right)\).
\(P = 1\);
\(P = - 1\);
\(P = 2\);
\(P = 0\).
Cho biết \(\tan \alpha = 2\). Giá trị của \(P = \frac{{2\sin \alpha - 2\cos \alpha }}{{2\cos \alpha + 3\sin \alpha }}\) bằng bao nhiêu?
\(P = 0\);
\(P = \frac{1}{4}\);
\(P = - \frac{1}{4}\);
\(P = \frac{2}{7}\).
Giá trị lượng giác nào dưới đây bằng với \[{\rm{cos67}}^\circ \]?
\(\sin 113^\circ \);
\({\rm{cos}}113^\circ \);
\(\sin 23^\circ \);
\({\rm{cos2}}3^\circ \).
Gọi \(K\) là chu vi tam giác \(ABC\) có \(a = 8\,\,cm,\,b = 5\,\,cm,\,\,\widehat C = 175^\circ \). Giá trị \(K\) của gần nhất với giá trị nào sau đây?
\(25\);
\(13\);
\(26\);
\(36\).
Cho tam giác \(ABC\) có \(AB = 5,\,\,BC = 7,\,\,AC = 8\). Độ dài bán kính đường tròn ngoại tiếp tam giác \(ABC\) là
\(\frac{{7\sqrt 3 }}{3}\);
\(\frac{{10\sqrt 3 }}{3}\);
\(7\sqrt 3 \);
\(10\sqrt 3 \).
Trong tam giác \(ABC\), phát biểu nào sau đây đúng?
\(\frac{a}{{\sin A}} = R\);
\(\frac{b}{{\sin 2B}} = R\);
\(\frac{c}{{\sin {C^2}}} = 2R\);
\(\frac{c}{{\sin C}} = 2R\).
Cho tam giác \(ABC\) có cạnh \(AB = 2cm,\widehat {ABC} = 60^\circ ,\widehat {BAC} = 75^\circ \) (như hình vẽ)
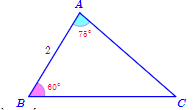
Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,\,c{m^2}\);
\(0,63\,\,c{m^2}\);
\(2,45\,\,c{m^2}\);
\(1,58\,\,c{m^2}\).
II. PHẦN TỰ LUẬN (3 điểm)
(1,0 điểm)
a) Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}| - 6 < 2x \le 8} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|\left| {x + 1} \right| \le 2} \right\}\). Tìm tập hợp \(\left( {{C_\mathbb{R}}A} \right)\backslash \left( {{C_\mathbb{R}}B} \right)\).
b) Cho hai tập hợp \(A = \left[ {1;8} \right]\) và \(B = \left\{ {x \in \mathbb{R}|m{x^2} - 2\left( {m + 1} \right)x + 3m + 3 = 0} \right\}\), với \(m \in \mathbb{R}\). Tìm m để tập \(B\) có đúng hai tập con đồng thời \(B \subset A\).
(1,0 điểm) Cho các địa điểm \(A,B\) và \(C\) (như hình vẽ) biết \(AB = 100\,\,km,\,AC = 150\,\,km,\widehat {ABC} = 110^\circ \). Bạn An muốn đi từ \(A\) đến \(C\) bằng một trong hai cách sau đây:
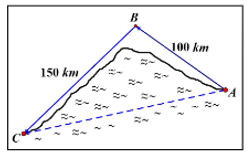
Cách 1: Đi tàu thủy từ \(A\) và \(C\) với vận tốc \(30\,\,km/h\).
Cách 2: Đi xe hơi từ \(A\) và \(B\) rồi từ \(B\) đến \(C\) với vận tốc \(50\,\,km/h\).
Hỏi đi cách nào thì An sẽ đến \(C\) sớm hơn?
(1,0 điểm)
Một người ăn kiêng muốn trộn hai loại thức ăn \(A\) và \(B\) để tạo ra một hỗn hợp chứa ít nhất \(50g\) protein, ít nhất \(130\,mg\) canxi và không quá \(550\,calo\). Giá trị dinh dưỡng của thức ăn loại \(A\) và \(B\) được cho trong bảng sau:
Thức ăn | Protein (g/ly) | Canxi (mg/ly) | Calo (ly) |
A | 20 | 20 | 100 |
B | 10 | 50 | 150 |
Biết rằng giá tiền một ly thức ăn loại \(A\) là \(110\,\,000\) đồng, một ly thức ăn loại \(B\) là \(60\,\,000\) đồng. Hỏi người ăn kiêng phải sử dụng bao nhiêu ly thức ăn mỗi loại để số tiền bỏ ra là ít nhất?








