Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 5
24 câu hỏi
I. PHẦN TRẮC NGHIỆM (7 điểm)
Phủ định của mệnh đề \(A:\) “Tất cả số thập phân đều là số hữu tỉ” là mệnh đề nào?
\(\overline A :\) “Có duy nhất một số thập phân không là số hữu tỉ”;
\(\overline A :\) “Tất cả số thập phân đều không là số hữu tỉ”;
\(\overline A :\) “Tất cả số hữu tỉ đều viết được dưới dạng số thập phân”;
\(\overline A :\) “Có ít nhất một số thập phân không phải là số hữu tỉ”.
Cho các câu sau:
(I) \(2\) là số nguyên;
(II) \(7x + \frac{1}{2}\) là một đa thức một biến;
(III). Cố đô Huế được Unesco công nhận là di sản văn hóa thế giới vào năm 1993;
(IV) \(x - 1 = \frac{1}{2}\);
(V) Hoa mười giờ nở vào đúng 10 giờ.
Có bao nhiêu câu không là mệnh đề?
0;
1;
3;
4.
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\): “Nếu a chia hết cho 2 thì a chia hết cho 4” là
Nếu a không chia hết cho 2 thì a không chia hết cho 4;
Nếu a chia hết cho 2 thì a không chia hết cho 4;
Nếu a không chia hết cho 4 thì a không chia hết cho 2;
Nếu a chia hết cho 4 thì a chia hết cho 2.
Cho bất phương trình\(x - 2y + 5 > 0\) có tập nghiệm là \(S\). Mệnh đề nào sau đây đúng?
\(\left( { - 2;\,2} \right) \in S\);
\(\left( {2;\,2} \right) \in S\);
\(\left( { - 2;\,4} \right) \in S\);
\(\left( {1;\,3} \right) \in S\).
Cho ba tập hợp \(A,\,\,B,C\) như hình bên dưới:
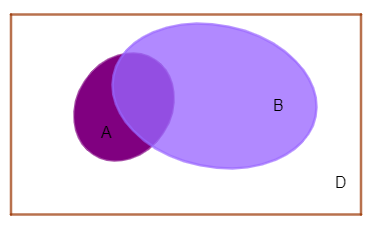
Phần không tô màu trong hình tương ứng với tập hợp nào sau đây?
\(D\);
\({C_D}\left( {A \cap B} \right)\);
\({C_D}\left( {A \cup B} \right)\);
\(A \cup B\).
Liệt kê các phần tử của tập hợp \(X = \left\{ {x \in \mathbb{R},x \ge 0|{x^2} - 2022 = 0} \right\}\).
\(X = \left\{ { - \sqrt {2022} ;\,\sqrt {2022} } \right\}\);
\(X = \left\{ { - 2022;\,\,2022} \right\}\);
\(X = \left\{ { - \sqrt {2022} } \right\}\);
\(X = \left\{ {\sqrt {2022} } \right\}\).
Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 2022 \le 2021 + 2x} \right\}\), \(B = \left\{ {x \in \mathbb{R}|3x - 6 \le 2x - 1} \right\}\). Có bao nhiêu số tự nhiên thuộc cả hai tập \(A\) và \(B\)?
\(5\);
\(6\);
\(7\);
\(4\).
Lớp 10D có \(45\) học sinh, trong đó có \(25\) em thích môn Văn, \(20\) em thích môn Toán, \(18\) em thích môn Tiếng Anh, \(6\) em không thích môn nào, \(5\) em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
\(34\);
\(11\);
\(20\);
\(1\).
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(2x - 5y + 3z \le 0\).
\(2x + 3y < 5\).
\(3{x^2} + 2x - 4 > 0\).
\(2{x^2} + 5y > 3\).
Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
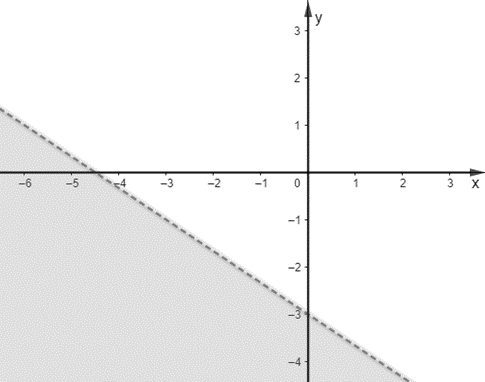
\[2x + 3y > - 9\].
\[3x + 2y \le - 9\].
\[3x + 2y > 6\].
\[2x + 3y < 9\].
Phần không gạch chéo ở hình sau đây (kể cả biên) là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn đáp án \[A\,,\,\,B\,,\,\,C\,,\,\,D\]?
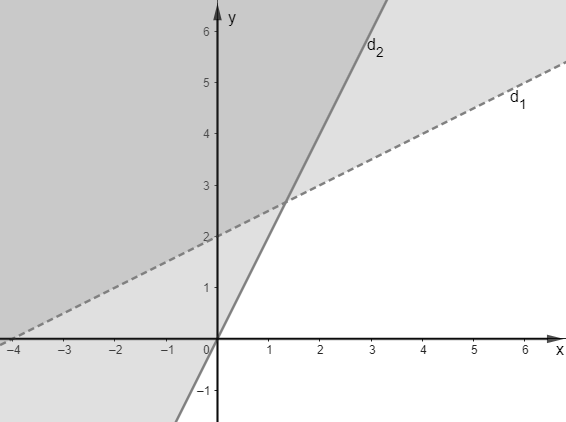
\(\left\{ \begin{array}{l}x - 2y > - 4\\x < 2y\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y \ge - 4\\x < 2y\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y > - 4\\2x \ge y\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y \ge - 4\\2x > y\end{array} \right.\).
Cho hệ bất phương trình: \(\left\{ \begin{array}{l}mx - 2y \le 5\\\left( {m - 1} \right)y \ge 3\end{array} \right.\). Tìm điều kiện của \(m\) để cặp số \(\left( {1;\,\,1} \right)\) là nghiệm của hệ bất phương trình.
\(\left[ {2;5} \right]\);
\(\left[ {2;7} \right]\);
\(\left( {4;5} \right)\);
\(\left[ {4;7} \right]\).
Cho tam giác \(ABC\) thỏa mãn \({\sin ^2}A = \sin B.\sin C\). Khẳng định nào dưới đây là đúng?
\[{\rm{cos}}\frac{A}{2} \le \frac{1}{2}\];
\[{\rm{cos}}A \ge \frac{1}{2}\];
\[{\rm{cos}}A = 0\];
\[{\rm{cos}}A < \frac{1}{2}\].
Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin 0^\circ + {\rm{cos}}0^\circ = 1\);
\({\sin ^2}30^\circ + {\rm{co}}{{\rm{s}}^2}60^\circ = 1\);
\(\sin 90^\circ + {\rm{cos9}}0^\circ = 1\);
\({\sin ^2}120^\circ + {\rm{co}}{{\rm{s}}^2}120^\circ = 1\).
Cho góc \(90^\circ < \alpha < 180^\circ \). Biết rằng \(\sin \alpha = \frac{1}{3}\). Tính giá trị của \(\cos \alpha \).
\(\cos \alpha = \frac{2}{3}\).
\(\cos \alpha = - \frac{2}{3}\).
\(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
\(\cos \alpha = \frac{{ - 2\sqrt 2 }}{3}\).
Cho tam giác \(ABC\) có \(AB = 2\,\,cm\), \(\widehat {ABC} = 60^\circ \), \(\widehat {BAC} = 75^\circ \). Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,\,c{m^2}\);
\(0,63\,\,c{m^2}\);
\(2,45\,\,c{m^2}\);
\(1,58\,\,c{m^2}\).
Từ vị trí \(A\) cách mặt đất \(1m\), một bạn nhỏ quan sát một cây đèn đường (hình vẽ).
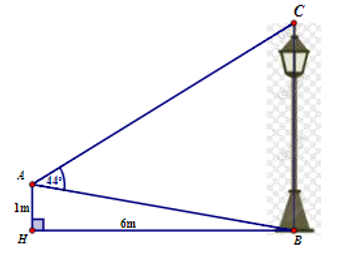
Biết \(HB = 6\,\,m\), \(\widehat {BAC} = 44^\circ \). Chiều cao của cây đèn đường gần nhất với giá trị nào sau đây?
\(5,1\,\,m\);
\(7,2\,m\);
\(5,9\,\,m\);
\(8,3\,\,m\).
Phát biểu nào dưới đây là đúng?
Vectơ là một tia có điểm gốc và có hướng;
Vectơ là một đường thẳng.
Vectơ là một đoạn thẳng có hướng.
Vectơ là một điểm.
Cho lục giác đều \(ABCDEF\) tâm \(O\). Số các vectơ bằng \(\overrightarrow {OC} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là
2;
3;
4;
6.
Cho hình thoi \(ABCD\) cạnh \(a\), \(\widehat {BAD} = 60^\circ \). Gọi \(O\) là giao điểm của hai đường chéo. Độ dài vectơ \(\overrightarrow {OA} - \overrightarrow {OC} \) là
\(2a\);
\(a\sqrt 3 \);
\(2a\sqrt 3 \);
\(a\).
Vectơ tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \) bằng
\(\overrightarrow {MN} \);
\(\overrightarrow {PN} \);
\(\overrightarrow {MR} \);
\(\overrightarrow {NP} \).
II. PHẦN TỰ LUẬN (3 điểm)
(1 điểm)
a) Xác định điều kiện của \(a,b\) để \(A \cap B = \emptyset \) với \(A = \left[ {a - 1;\,\,a + 2} \right]\) và \(B = \left( {b;\,\,b + 4} \right]\).
b) Xác định điều kiện của \(a\) để \(E \subset \left( {C \cup D} \right)\) với \(C = \left[ { - 1;\,\,4} \right];\,\,D = \mathbb{R}\backslash \left( { - 3;\,\,3} \right)\) và \(E = \left[ {a - 2;\,\,a} \right]\).
(1 điểm)
Cho tam giác \[ABC\] có trọng tâm \[G\]và hai đường trung tuyến \(AM\,,\,\,BN\). Biết rằng \(AM = 15\), \(BN = 12\) và tam giác \[CMN\]có diện tích bằng \(15\sqrt 3 \). Tính độ dài đoạn thẳng \(MN\).
(1 điểm)
Một trang trại cần thuê xe vận chuyển ít nhất \(450\) con lợn và \(35\) tấn cám. Nơi cho thuê xe chỉ có không quá \(12\) xe lớn và \(10\) xe nhỏ. Một chiếc xe lớn có thể chở \(50\) con lợn và \(5\) tấn cám. Một chiếc xe nhỏ có thể chở \(30\) con lợn và \(1\) tấn cám. Tiền thuê một xe lớn là \(4\) triệu đồng, một xe nhỏ là \(2\) triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?








