Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 4
24 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Hình nào sau đây minh họa \[A\] là tập con của \[B\]?
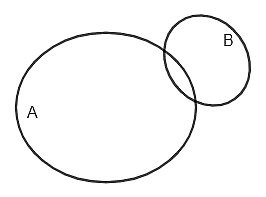
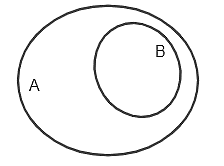
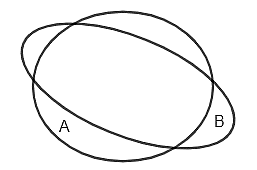
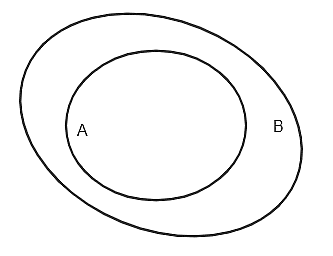
Điểm \[A\left( { - 1;\,3} \right)\] là điểm thuộc miền nghiệm của bất phương trình:
\[ - 3x + 2y - 4 > 0\];
\[x + 3y < 0\];
\[3x - y > 0\];
\[2x - y + 4 > 0\].
Trong các câu sau, câu nào không phải là mệnh đề?
\[5 + 2 = 8\];
\[{x^2} + 2 > 0\];
\[4 - \sqrt {17} > 0\];
\[5 + x = 2\].
Cho tam giác \[ABC\] có \(AB = c,AC = b,BC = a\), \(R\) là bán kính đường tròn ngoại tiếp tam giác \[ABC\], \(r\) là bán kính đường tròn nội tiếp tam giác \[ABC\], \(S\) là diện tích tam giác \[ABC\], \(p\) là nửa chu vi tam giác \[ABC\]. Khẳng định nào sau đây là đúng?
\[S = \frac{{abc}}{{4r}}\];
\[r = \frac{{2S}}{{a + b + c}}\];
\[{a^2} = {b^2} + {c^2} + 2bc\cos A\];
\[S = r\left( {a + b + c} \right)\].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\[{x^2} + y - 2 > 6\];
\[3{x^2} + 2{y^2} < 1\];
\[x + y - z \ge 0\];
\[16x + 25y \ge 4\].
Trong các đẳng thức sau đây, đẳng thức nào đúng?
\[\sin 120^\circ = \frac{{ - \sqrt 3 }}{2}\];
\[\cos 120^\circ = \frac{1}{2}\];
\[\tan 120^\circ = - \sqrt 3 \];
\[\cot 120^\circ = \sqrt 3 \].
Câu nào sau đây là một mệnh đề?
I. \[3 + 4 \ge 2\]. II. \[\exists x:{x^2} - 3x + 4 = 0\]. III. \[\forall x,{x^2} + 6x + 5 = 0\].
Chỉ I và II.
Chỉ I và III.
Chỉ II và III.
Cả I, II và III.
Cho \[\alpha \] là góc tù. Khẳng định nào sau đây là sai?
\[\cos \alpha < 0\];
\[\sin \alpha < 0\];
\[\tan \alpha < 0\];
\[\cot \alpha < 0\].
Cho hai tập hợp \[A = \left\{ {1;\,2;\,3} \right\}\] và \[B = \left\{ {1;\,2;\,3;\,4;\,5} \right\}\]. Có tất cả bao nhiêu tập \[X\] thỏa mãn \[A \subset X \subset B\]?
\[4\];
\[5\];
\[6\];
\[8\].
Giá trị của biểu thức \[P = \cos 30^\circ .\cos 60^\circ - \sin 30^\circ .\sin 60^\circ \] là?
\[P = \sqrt 3 \];
\[P = \frac{{\sqrt 3 }}{2}\];
\[P = 1\];
\[P = 0\].
Phần không gạch trong hình vẽ (không kể biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
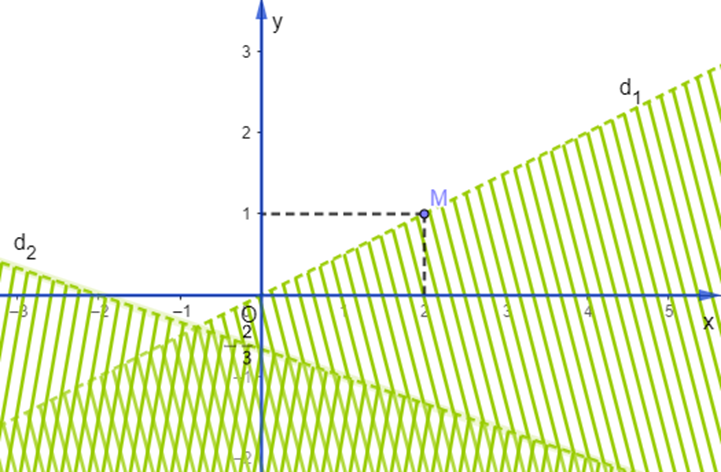
\[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\end{array} \right.\].
Mệnh đề nào sau đây tương đương với mệnh đề \[A \ne \emptyset \]?
\[\forall x,\,x \in A\];
\[\exists x,\,x \in A\];
\[\exists x,\,x \notin A\];
\[\forall x,\,x \subset A\].
Vectơ nào sau đây là vectơ không?
\[\overrightarrow {AB} \] (\[A\] và \[B\] phân biệt);
\[\overrightarrow {CB} \] (\[C\] và \[B\] phân biệt);
\[\overrightarrow {MN} \] (\[M\] và \[N\] phân biệt);
\[\overrightarrow {PP} \].
Cho tập \[A = \left\{ {0;1;\,2;\,3;\,4;\,5;\,6} \right\}\] có bao nhiêu tập hợp con của tập \(A\) có đúng hai phần tử mà gồm các số chẵn?
4;
6;
7;
8.
Cho hình bình hành \[ABCD\] tâm \[O\]. Khẳng định nào sau đây sai?
\[\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \];
\[\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \];
\[\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \];
\[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \].
Cho 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \]. Mệnh đề nào sau đây đúng?
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] cùng phương thì chúng cùng hướng.
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] cùng hướng thì chúng cùng phương;
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] bằng nhau thì chúng ngược hướng;
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] đối nhau thì chúng cùng hướng.
Tập hợp \[A = \left\{ {{k^2} + 1\left| {k \in \mathbb{Z},\,\left| k \right| \le 2} \right.} \right\}\] có bao nhiêu phần tử?
1;
2;
3;
5.
Cho hình chữ nhật \[ABCD\], \[M\] là trung điểm \[AB\]. Biết \[AB = 2a,\,AD = a\]. Độ dài vectơ \[\overrightarrow {MD} \] là bao nhiêu?
\[\frac{1}{2}a\];
\[a\];
\[a\sqrt 2 \];
\[2a\].
Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?
![Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/11/7-1762495747.png)
![Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/11/8-1762495761.png)
![Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/11/9-1762495776.png)
![Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? (ảnh 5)](https://video.vietjack.com/upload2/quiz_source1/2025/11/10-1762495786.png)
Trên sườn đồi, với độ dốc \[12\% \] (độ dốc của sườn đồi được tính bằng tan góc nhọn tạo bởi sườn đồi với phương ngang) có một cây cao mọc thẳng đứng. Ở phía chân đồi, cách gốc cây \[30\]m, người ta nhìn ngọn cây dưới một góc \[45^\circ \] so với phương ngang. Hỏi chiều cao của cây là bao nhiêu (làm tròn đến hàng đơn vị, theo đơn vị mét)?
\[26\];
\[30\];
\[6\];
\[15\].
“Nếu \[a\] và \[b\] là hai số hữu tỉ thì tổng \[a + b\] cũng là số hữu tỉ”. Mệnh đề nào sau đây là mệnh đề tương đương với mệnh đề đó?
Điều kiện cần để tổng \[a + b\] là số hữu tỉ là cả hai số \[a\] và \[b\] đều là số hữu tỉ.
Điều kiện đủ để tổng \[a + b\] là số hữu tỉ là cả hai số \[a\] và \[b\] đều là số hữu tỉ.
Điều kiện cần để cả hai số \[a\] và \[b\] hữu tỉ là tổng \[a + b\] là số hữu tỉ.
Tất cả các câu trên đều sai.
II. TỰ LUẬN (3 ĐIỂM)
(1,0 điểm) Cho 2 tập hợp \[A = \left[ { - 3;\,6} \right],\,B = \left[ {2m - 4;\,2m + 3} \right)\].
a) Tìm tập hợp \[A \cap \mathbb{Z}\].
b) Tìm \[m\] để \[A \cap B = \emptyset \].
(1,0 điểm) Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa \[24\]g hương liệu, \[9\]lít nước và \[210\]g đường để pha chế nước cam và nước táo. Để pha \[1\]lít nước cam cần \[30\]g đường, \[1\]lít nước và \[1\]g hương liệu. Để pha \[1\]lít nước táo cần \[10\]g đường, \[1\]lít nước và \[4\]g hương liệu. Mỗi lít nước cam nhận được \[60\] điểm thưởng, mỗi lít nước táo nhận \[80\] điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm cao nhất?
(1,0 điểm) Khu vườn nhà anh T có dạng miền tứ giác \[ABCD\] với các kích thước đo đạc được ghi trên hình vẽ bên dưới:
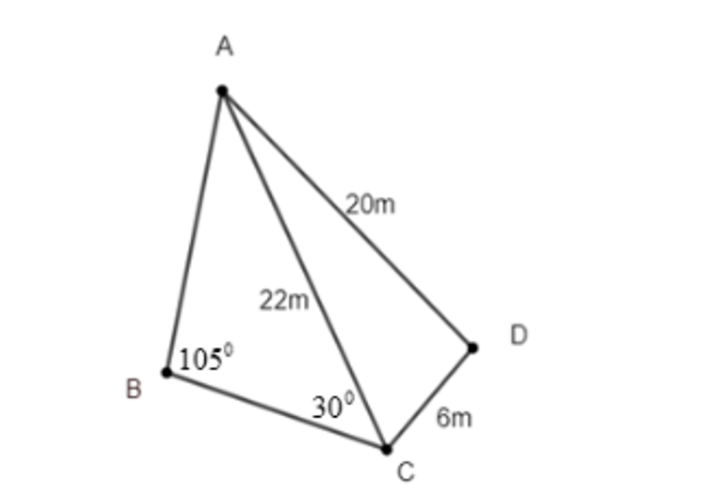
a) Tính khoảng cách từ điểm \[A\] đến điểm \[B\] (kết quả làm tròn một chữ số thập phân).
b) Tính diện tích khu vườn đó (kết quả làm tròn một chữ số thập phân).








