Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 3
24 câu hỏi
I. TRẮC NGHIỆM (7 Điểm)
Hai vectơ được gọi là bằng nhau khi và chỉ khi
hai vectơ đó cùng hướng và cùng độ dài;
hai vectơ đó cùng phương;
hai vectơ đó cùng độ dài;
hai vectơ đó cùng phương và cùng độ dài.
Điểm \(O\left( {0;\,\,0} \right)\) thuộc miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
\(\left\{ \begin{array}{l}3x > 0\\2x - y > 1\end{array} \right.\);
\(\left\{ \begin{array}{l}2x + 4y < 1\\x - 3y + 2 \le 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y + 1 \ge 0\\3x - 4y > - 2\end{array} \right.\);
\(\left\{ \begin{array}{l}2x + y < 0\\4x - 3y \ge 0\end{array} \right.\).
Trong các bất phương trình sau bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(x - 3y + 4 = 0\);
\({x^2} - y < 5\);
\(x + 2y - 3 > 0\);
\(x - 3{y^3} + 4 \le 0\).
Biểu diễn tập hợp \(A = \left\{ {x \in \mathbb{R},2 \le x \le 5} \right\}\) trên trục số ta được




Đẳng thức nào sau đây sai?
\(\cot \left( {180^\circ - \alpha } \right) = - \cot \alpha \);
\[\cos \left( {180^\circ - \alpha } \right) = \cos \alpha \];
\(\sin \left( {180^\circ - \alpha } \right) = \sin \alpha \);
\(\tan \left( {180^\circ - \alpha } \right) = - \tan \alpha \)..
Cho hình bình hành \(ABCD\) trong các khẳng định sau, khẳng định nào sai?
\(\overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {CB} \);
\(\overrightarrow {DC} + \overrightarrow {DA} = \overrightarrow {DB} \);
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {BC} \);
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
Cho góc \(\alpha \in \left( {0^\circ ;\,\,90^\circ } \right)\) kết luận nào sau đây đúng?
\(\sin \alpha > 0\);
\(\tan \alpha < 0\);
\(\cot \alpha < 0\);
\[\cos \alpha < 0\].
Cho tam giác \(ABC\) có độ dài ba cạnh \(AB = c\), \(BC = a\), \(AC = b\), \(R\) là bán kính đường kính đường tròn ngoại tếp tam giác, \(S\)là diện tích tam giác \(ABC\). Khẳng định nào sau đây sai?
\(a = \frac{{b.\sin A}}{{\sin B}}\);
\(S = \frac{{abc}}{{2R}}\);
\[\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\];
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\).
Cho tập hợp \(A = \left\{ { - 2;\,\,1;\,\,3;\,\,5;\,\,6} \right\}\) và\(B = \left\{ {3;\,\,5;\,\,7;\,\,8} \right\}\)phần tử thuộc tập \(A \cap B\) là
\(6\);
\(7\);
\(3\);
\(1\).
Trong các câu sau, câu nào không phải là mệnh đề?
Hà Nội là thủ đô của Việt Nam;
Hình chữ nhật có hai đường chéo vuông góc với nhau;
2 là số nguyên tố;
Hôm nay là thứ mấy?.
Cho ba điểm \(A,\,\,B,\,\,C\) cùng nằm trên một đường thẳng. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng khi và chỉ khi
Điểm \(B\)thuộc đoạn thẳng \(AC\);
Điểm \(A\) nằm ngoài đoạn thẳng \(BC\);
Điểm \(A\) thuộc đoạn thẳng \(BC\);
Điểm \(C\) thuộc đoạn thẳng \(AB\).
Cho mệnh đề A: “\[\forall x \in \mathbb{R},{x^2} - x + 7 < 0\]”. Mệnh đề phủ định của A là:
;
;
;
.
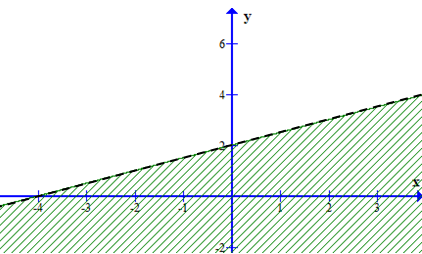
Phần không bị gạch (kể cả biên) trong hình dưới đây biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
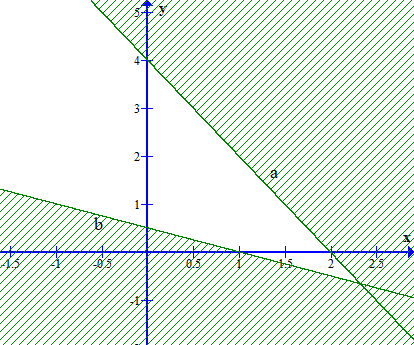
\(\left\{ \begin{array}{l}2x + y \ge 1\\x + 2y \le 4\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 2y \ge 1\\2x + y \le 4\end{array} \right.\);
\(\left\{ \begin{array}{l}2x + y \le 1\\x + 2y \ge 4\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 2y \le 1\\2x + y \ge 4\end{array} \right.\).
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ;
Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn;
Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn;
Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
Miền nghiệm của bất phương trình \(x - 2y + 4 < 0\) là phần không bị gạch trong hình vẽ nào dưới đây
A. 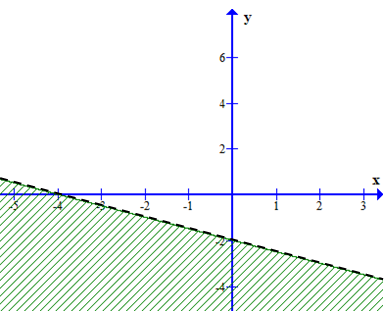
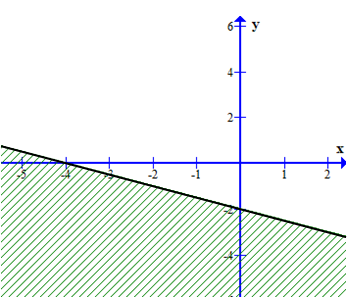
C. 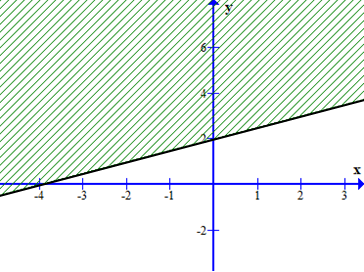
Cho tập hợp \(A = \left( { - \infty ;\,\,5} \right)\) và \(B = \left[ { - 1;\,\, + \infty } \right)\). Tập hợp nào là tập con của tập \(A \cap B\)?
\(\left[ { - 1;\,\,4} \right]\);
\(\left[ {5;\,\, + \infty } \right)\);
\(\left( { - \infty ;\,\, - 1} \right)\);
\(\left( { - 1;\,\,5} \right]\).
Cho \(\cot \alpha = \frac{1}{3}\), giá trị của biểu thức\(A = \frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}\)bằng
\(13\);
\(\frac{{15}}{{13}}\);
\( - \frac{{15}}{{13}}\);
\( - 13\).
Cho tập hợp \(A = \left\{ {a;\,\,b;\,\,c} \right\}\) số tập con có hai phần tử của tập \(A\) là
\(4\);
\(3\);
\(1\);
\(2\).
Cho hình bình hành \(ABCD\), tâm \(O\). Vectơ \(\overrightarrow {BA} + \overrightarrow {DA} + \overrightarrow {AC} \) bằng
\(\overrightarrow {BC} \);
\(2\overrightarrow {DA} \);
\(\overrightarrow 0 \);
\(\overrightarrow {BD} \).
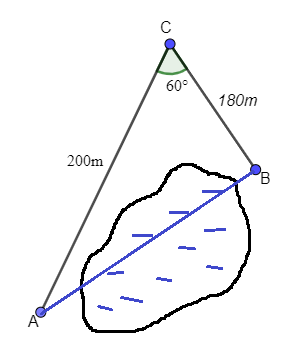
Khoảng cách từ \(A\) đến \(B\) không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được điểm \(C\) mà từ đó có thể nhìn được \(A\) và \(B\) dưới một góc \({60^o}\). Biết \(CA = 200m\), \(CB = 180m\). Tính khoảng cách \(AB\).
\(36\,\,400m\);
\(228m\);
\(20\sqrt {91} m\);
\(25\sqrt {91} m\).
Lớp \(10A\) có \(45\) học sinh, trong đó có \(15\) học sinh được xếp loại học lực giỏi, \(20\) học sinh được xếp loại hạnh kiểm tốt, \(10\) em vừa xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc có hạnh kiểm tốt?
\(45\);
\(35\);
\(25\);
\(10\).
II. TỰ LUẬN (3 Điểm)
(1,0 điểm) Cho tập hợp \(A = \left( { - \infty ;m + 1} \right]\) và \(B = \left( { - 2;\, + \infty } \right)\).
a) Xác định tập \(A \cap B\) với \(m = 2\).
b) Xác định \(m\) để \(A \cap B = \emptyset \).
(1,0 điểm) Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa \(20kg\) gạo nếp, \(2kg\) thịt ba chỉ và \(5kg\) đậu xanh để gói bánh trưng và bánh ống. Để gói một cái bánh trưng cần \(0,4kg\), gạo nếp, \(0,05kg\) thịt ba chỉ và \(0,1kg\) đậu xanh. Để gói một cái bánh ống cần \(0,6kg\) gạo nếp, \(0,075kg\) thịt ba chỉ và \(0,15kg\) đậu xanh. Mỗi cái bánh trưng được \(5\) điểm thưởng, mỗi cái bánh ống được \(6\) điểm thưởng. Vậy cần phải gói mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất.
(1,0 điểm) Cho tam giác \(ABC\) có \(AB = 4\), \(AC = 10\) và đường trung tuyến \(AM = 6\). Tính độ dài cạnh \(BC\) và diện tích tam giác \(ABC\).








