Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 2
24 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Trong các câu sau câu nào là mệnh đề đúng?
\[\sqrt 2 \] là số vô tỉ;
\[5 + 3 < 7\];
\[100\]tỉ là số nguyên lớn nhất;
Trời hôm nay đẹp quá!.
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d)?
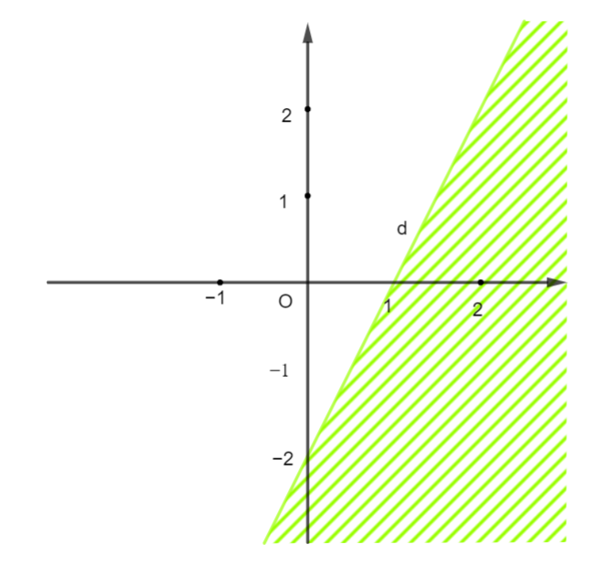
\[2x - y \le 2\];
\[2x - 3y \le 0\];
\[2x + y < 2\];
\[2x - y > 2\].
Trong các mệnh đề sau mệnh đề nào là mệnh đề sai?
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] cân;
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] cân và có một góc \[60^\circ \];
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] có ba cạnh bằng nhau;
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \] Tam giác \[ABC\] có hai góc bằng \[60^\circ \].
Cho hai tập hợp: \[C = \left\{ {x \in \mathbb{R}|x \ge 3} \right\}\]và\[D = \left\{ {x \in \mathbb{R}|x > 3} \right\}\]. Tìm mệnh đề sai?
\[C \subset \mathbb{R}\];
\[C \subset D\];
\[D \subset C\];
\[D \subset \mathbb{R}\].
Cho tập hợp\[B = \left\{ {x \in \mathbb{Z}|{x^2} - 4 = 0} \right\}\]. Tập hợp nào sau đây đúng?
\[B = \left\{ {2;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 2;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 4;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 2;{\rm{ 2}}} \right\}\].
Cho mệnh đề . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề
A?A. ;
;
;
.
Cho hai tập hợp \[P = \{ 1;\,3;\,5;\,7;\,9\} \]và \[Q = \{ 0;\,2;\,4;\,5;\,6;\,8\} \]. Số phần tử của tập hợp \[P \cup Q\]là:
\[0\];
\[1\];
\[10\];
\[11\].
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 \le 0\end{array} \right.\]. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
\[M\left( {0;\,1} \right)\];
\[N\left( { - 1;\,1} \right)\];
\[P\left( {1;\,3} \right)\];
\[Q\left( { - 1;\,0} \right)\].
Trong tam giác \[ABC\]. Khẳng định nào sau đây là đúng?
\[sinA = sin\left( {B + C} \right)\];
\[cosA = cos\left( {B + C} \right)\];
\[cosA > 0\];
\[sinA \le 0\].
Cho góc \[\alpha \] thỏa mãn \[\sin \alpha + \cos \alpha = \sqrt 2 \]. Giá trị của \[\tan \alpha + \cot \alpha \]là:
\[1\];
\[ - 2\]\[;\]
\[0\]\[;\]
\[2\].
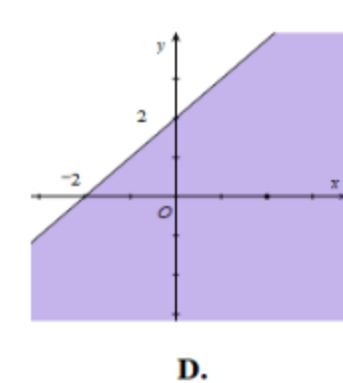
Miền nghiệm của bất phương trình \[x + y \le 2\] là phần tô đậm (kể cả biên) trong hình vẽ nào sau đây?
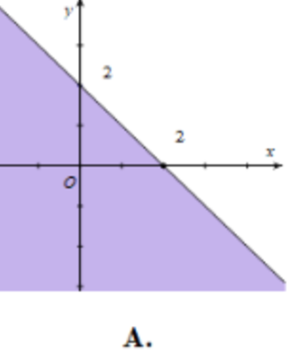
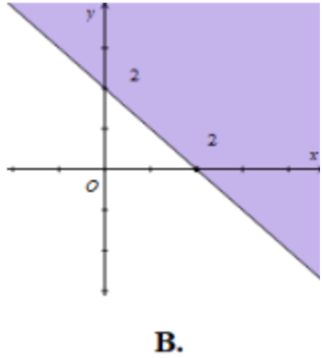
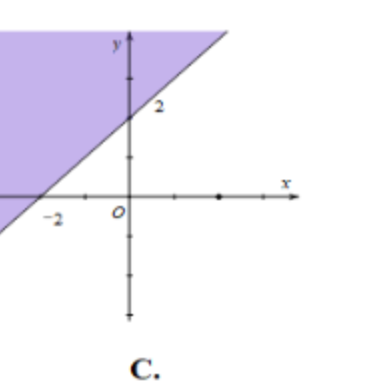
Cho hai tập hợp \[A = \left( { - 4;\,1} \right],{\rm{ }}B = \left[ { - 3;\,m} \right)\] khác rỗng. Tìm \[m\] để \[A \cup B = A\].
\[m \le 1\];
\[m = 1\];
\[ - 3 \le m \le 1\];
\[ - 3 < m \le 1\].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\[2{x^2} + 3y > 0\];
\[{x^2} + {y^2} < 2\];
\[x + {y^2} \ge 0\];
\[x + y \ge 0\].
Cho tam giác \[ABC\] có các cạnh \[AB = c;{\rm{ }}BC = a;{\rm{ }}AC = b\]. Tính góc \[\widehat {BCA}\] của tam giác \[ABC\] biết \[a \ne b\] và ?
\[\widehat {BCA} = 120^\circ \];
\[\widehat {BCA} = 60^\circ \];
\[\widehat {BCA} = 30^\circ \];
\[\widehat {BCA} = 135^\circ \].
Hình bình hành \[ABCD\] là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau đây?
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BC} } \right|\];
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\];
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right|\];
\[\overrightarrow {AC} = \overrightarrow {BD} \].
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \[A\], đi thẳng theo hai hướng tạo với nhau góc \[60^\circ \]. Tàu \[B\] chạy với tốc độ \[20\] hải lí một giờ. Tàu \[C\] chạy với tốc độ \[15\] hải lí một giờ (tham khảo hình vẽ). Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây?
\[61\] hải lí;
\[36\] hải lí;
\[21\] hải lí;
\[18\] hải lí.
Cho tam giác \[ABC\] đều cạnh \[2a\], bán kính đường tròn nội tiếp tam giác \[ABC\] là:
\[\frac{a}{{\sqrt 3 }}\];
\[\frac{{3a}}{{\sqrt 3 }}\];
\[\frac{{5a}}{{\sqrt 3 }}\];
\[\frac{{7a}}{{\sqrt 3 }}\].
Cho 3 điểm \[M,{\rm{ }}N,{\rm{ }}P\]. Mệnh đề nào sau đây đúng?
\[\overrightarrow {MN} + \overrightarrow {MP} = \overrightarrow {NP} \];
\[\overrightarrow {MN} + \overrightarrow {PM} = \overrightarrow {NP} \]\[;\]
\[\overrightarrow {NM} + \overrightarrow {PN} = \overrightarrow {PM} \]\[;\]
\[\overrightarrow {MN} - \overrightarrow {MP} = \overrightarrow {NP} \].
Mệnh đề nào sau đây đúng?
Có duy nhất một vectơ cùng phương với mọi vectơ\[;\]
Có ít nhất hai vectơ có cùng phương với mọi vectơ\[;\]
Có vô số vectơ có cùng phương với mọi vectơ\[;\]
Không có vectơ có nào cùng phương với mọi vectơ.
Kết quả bài toán tính: \[\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {DA} + \overrightarrow {BC} \] là:
\[\overrightarrow {DB} \];
\[2\overrightarrow {BD} \];
\[\overrightarrow 0 \];
\[ - \overrightarrow {AD} \].
Cho \[A = ( - \infty ;\,1\left] {,{\rm{ }}B = } \right[1;\, + \infty ),{\rm{ }}C = \left( {0;\,1} \right]\]. Khẳng định nào sau đây sai?
\[A \cap B \cap C = 1\];
\[A \cup B \cup C = \left( { - \infty ;\, + \infty } \right)\];
\[A{\rm{ }} \cup B\backslash C = \left( { - \infty ;\,0} \right] \cup \left[ {1;\, + \infty } \right)\];
\[A \cap B\backslash C = C\].
II. TỰ LUẬN (3 ĐIỂM)
(1,0 điểm) Cho tập hợp \[C = \left[ { - 3;\,8} \right]\] và \[D = \left[ {m - 3;\,8} \right]\].
a) Cho tập hợp \[A = \left( { - \infty ;\, - 3} \right]\] và \[A\backslash C = B\]. Tìm \[B\].
b) Với giá trị nào của m thì \[C \cap D\] là một đoạn thẳng có độ dài bằng 4.
(1,0 điểm) Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới với vốn đầu tư không quá \[72\] triệu đồng. Loài dài tay mua vào \[800.000\] đồng và lãi \[150.000\]một áo, loại ngắn tay mua vào \[600.000\] đồng và lãi \[120.000\]một áo. Cửa hàng ước tính nhu cầu của khách không quá 100 cái cho cả 2 loại. Lập phương án kinh doanh sao cho lãi nhất.
(1,0 điểm) Cho tam giác \[ABC\] có hai trung tuyến kẻ từ \[A\] và \[B\] vuông góc. Chứng minh rằng:
a) \[{a^2} + {b^2} = 5{c^2}\].
b) \[cotC = 2\left( {cotA + cotB} \right)\].








