Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 10
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tập hợp \(A\). Trong các mệnh đề sau, tìm mệnh đề nào sai?
\(\not \bigcirc \subset A\).
\(A \subset A\).
\(A \in A\).
\(A \ne \left\{ A \right\}\).
Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 \le 0\end{array} \right.\]
\[\left( {--1;1} \right)\].
\[\left( {0;1} \right)\].
\[\left( {--1;0} \right)\].
\[\left( {1;3} \right)\].
Cho tập hợp\[A{\rm{ }} = \left\{ {a,b,c,d} \right\}\]. Tìm số tập con của tập \[A{\rm{ }}\].
\[10\].
\[12\].
\[16\].
\[15\].
Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?
Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
Hình thang có hai cạnh bên bằng nhau là hình thang cân.
\(\pi \) là một số hữu tỉ.
Bạn có chăm học không?
Miền nghiệm của bất phương trình \[5\left( {x + 2} \right) - 9 < 2x - 2y + 7\;\;\] là phần mặt phẳng không chứa điểm nào?
\[\left( { - 2;1} \right)\].
\[\left( {2; - 1} \right)\].
\[\left( {0;0} \right)\].
\[\left( {2;3} \right)\].
Tập nghiệm của bất phương trình \(3x - 2y + 1 < 0\).
Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng \(3x - 2y + 1 = 0\)(bao gồm đường thẳng).
Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng \(3x - 2y + 1 = 0\)(không bao gồm đường thẳng).
Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng \(3x - 2y + 1 = 0\)(không bao gồm đường thẳng).
Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng \(3x - 2y + 1 = 0\)(bao gồm đường thẳng).
Cho \(A = \left\{ {x \in \mathbb{N}\,|\,x \le 3} \right\}\), \(B = \left\{ {0;\,\,1;\,\,2;\,\,3} \right\}\). Tập \(A \cap B\) bằng
\(\left\{ {0;\,1;\,2} \right\}\).
\(\left\{ {0;\,1;\,2;\,3} \right\}\).
\(\left\{ { - 3; - 2; - 1;0;1;2;3} \right\}\).
\(\left\{ {1;\,2;\,3} \right\}\).
Gọi là tập hợp các điểm trong mặt phẳng tọa độ \(\left( S \right)\) thỏa mãn hệ \(\left\{ \begin{array}{l}x - y - 1 \le 0\\x + 4y + 9 \ge 0\\x - 2y + 3 \ge 0\end{array} \right.\) (hình vẽ).
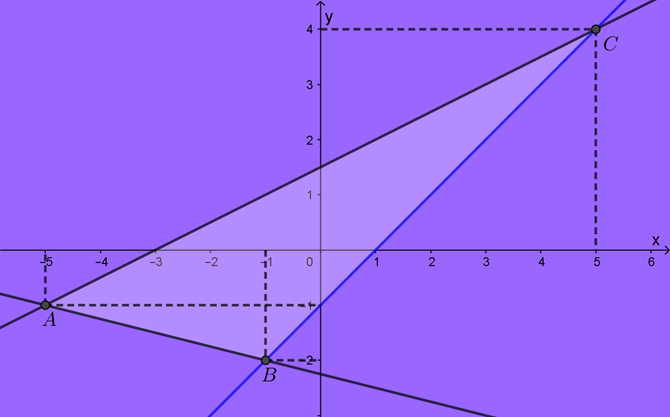
Tìm tọa độ \(\left( {x;y} \right)\) trong miền \(\left( S \right)\) sao cho biểu thức \(T = 3x - 2y - 4\) có giá trị nhỏ nhất.
\(\left( { - 1; - 2} \right)\).
\(\left( { - 2;5} \right)\).
\(\left( { - 5; - 1} \right)\).
\(\left( {5;4} \right)\).
Biết \[\cos \alpha = \frac{1}{3}\]. Giá trị đúng của biểu thức \[P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \] là:
\[\frac{1}{3}\].
\[\frac{{10}}{9}\].
\[\frac{4}{3}\].
\[\frac{{11}}{9}\].
Cho \[\sin \alpha = \frac{4}{5}\,\,\left( {{{90}^0} < \alpha < {{180}^0}} \right)\]. Tính \[{\rm{cos}}\alpha \]
\[c{\rm{os}}\alpha = \frac{3}{5}\].
\[c{\rm{os}}\alpha = \frac{5}{3}\]
\[c{\rm{os}}\alpha = - \frac{3}{5}\].
\[{\rm{cos}}\alpha = - \frac{4}{5}\]
Tam giác \(ABC\)có góc \(A\) nhọn, \(AB = 5\), \(AC = 8\), diện tích bằng \(12.\) Tính độ dài cạnh \(BC.\)
\(4\).
\(3\sqrt 2 \).
\(5\).
\(2\sqrt 3 \).
Hai chiếc xe cùng xuất phát ở vị trí A, đi theo hai hướng tạo với nhau một góc \({60^0}\). Xe thứ nhất chạy với tốc độ \(30km/h\), xe thứ hai chạy với tốc độ \(40km/h\). Hỏi sau 1h, khoảng cách giữa 2 xe là:
\(10\sqrt {13} \).
\(15\sqrt 3 km\).
\(13km\).
\(15km\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét bất phương trình \( - 2x + y - 2 < 0\). Xét tính đúng-sai của các khẳng định sau.
a) Cặp số \(( - 5; - 4)\) không là nghiệm của bất phương trình.
b) Miền nghiệm của bất phương trình chứa đường thẳng \(d: - 2x + y - 2 = 0\).
c) Miền nghiệm là nửa mặt phẳng chứa điểm \(( - 2; - 3)\) và không chứa đường thẳng \(d: - 2x + y - 2 = 0\).
d) Cặp số \((6;7)\) không là nghiệm của bất phương trình.
Cho \(A\) là tập hợp các học sinh lớp 10 đang học ở trường em và \(B\) là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Vậy:
a) \(A \cup B\)là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
b) \(A \cap B\)là tập hợp các học sinh lớp 10 hoặc học môn Tiếng Anh ở trường em.
c) \(A\backslash B\)là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
d) \(B\backslash A\)là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời từ câu 1 đến câu 4.
Một lớp 10C có 40 học sinh, trong đó có 21 học sinh thích môn Toán, 15 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp \(10C\) có bao nhiêu học sinh không thích cả hai môn trên?
Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 hecta (ha). Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu ha ngô để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh
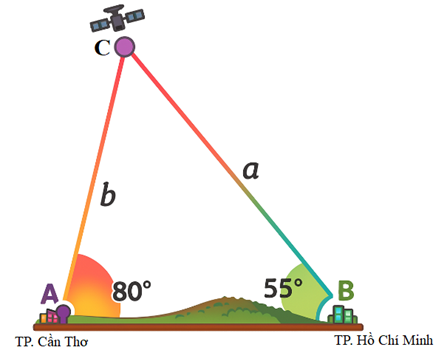
Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là \({55^^\circ }\) tại thành phố Hồ Chí Minh và \({80^^\circ }\) tại Cần Thơ. Hỏi khi đó vệ tinh cách trạm quan sát tại Cần THơ bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 127 km (làm tròn kết quả đến hàng đơn vị)
Cho hai tập hợp \(A = (m - 1;5);B = (3; + \infty ),m \in \mathbb{R}\). Tập hợp tất cả các giá trị của \(m\) để \(A\backslash B = \emptyset \) là tập hợp có dạng \(\left[ {a;b} \right)\). Tính \(b - a\).
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Một xưởng cơ khí có hai công nhân là Đạo và Lập. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi \(900\)nghìn đồng, mỗi sản phẩm II bán lãi \(700\)nghìn đồng.Để sản xuất được một sản phẩm I thì Đạo phải làm việc trong \(6\)giờ, Lập phải làm việc trong \(4\)giờ.Để sản xuất được một sản phẩm II thì Đạo phải làm việc trong \(7\)giờ, Lập phải làm việc trong \(3\)giờ.Một người không thể làm được đồng thời hai sản phẩm.Biết rằng trong một tuần Đạo không thể làm việc quá \(70\)giờ và Lập không thể làm việc quá \(40\)giờ.Tìm số tiền lãi lớn nhất có thể đạt được trong một tuần của xưởng.
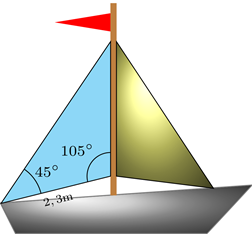
Tính diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dà\(2,3\)i một cạnh là m và hai góc kề cạnh đó có số đo là \({45^^\circ }\) và \({105^^\circ }\).
Cho \(\alpha \left( {{0^ \circ } \le \alpha \le {{180}^0}} \right)\) sao cho \(\cos \alpha = - \frac{3}{5}\). Hãy tính \(\sin \alpha \), \(\tan \alpha \), \(\cot \alpha \).








