Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 1
24 câu hỏi
PHẦN I. TRẮC NGHIỆM (7 điểm)
Trong các câu sau, câu nào là mệnh đề đúng?
Làm ơn hãy im lặng!;
Tháp Eiffel nằm ở Anh;
Biển ở Phú Quốc thật đẹp;
\(11\) là số nguyên tố.
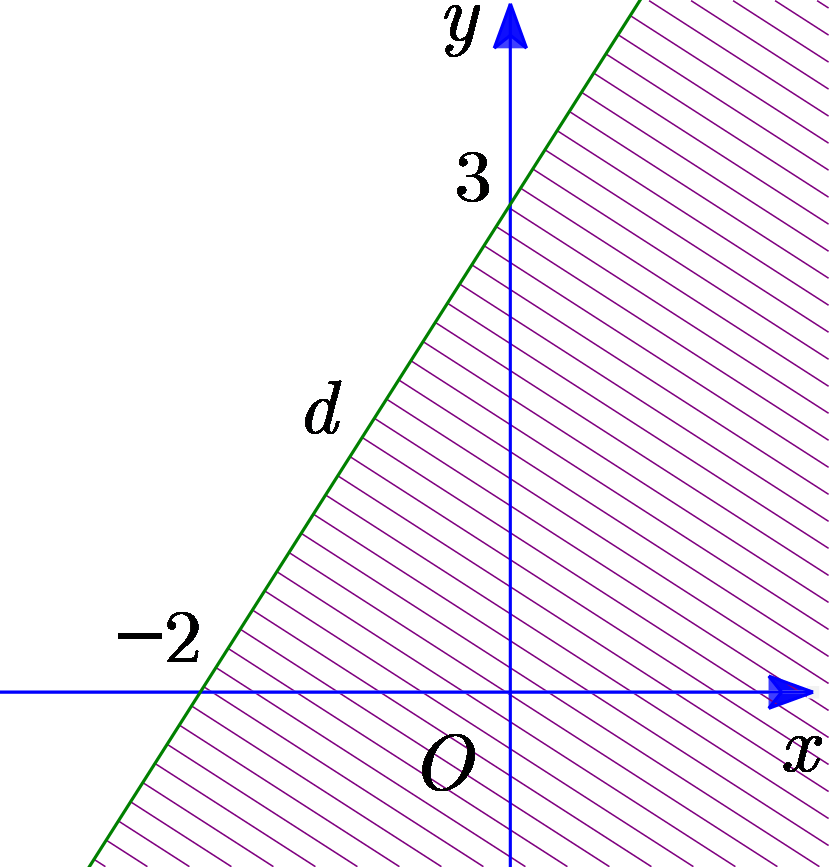
Trong hình vẽ dưới, phần mặt phẳng không bị gạch sọc (kể cảbiên) là miền nghiệm của hệ bất phương trình nào dưới đây?
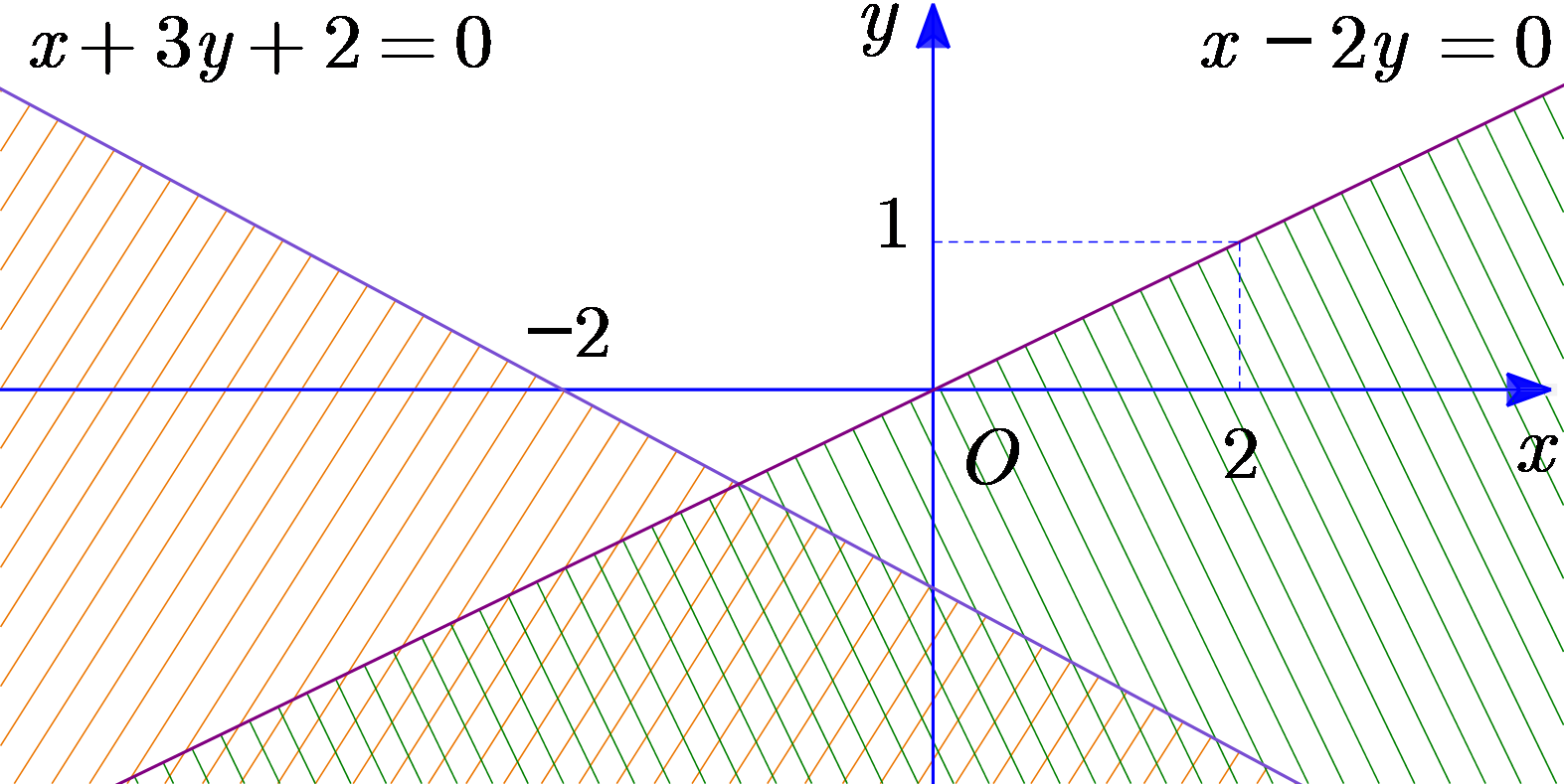
\(\left\{ \begin{array}{l}x - 2y \ge 0\\x + 3y \ge - 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y \ge 0\\x + 3y \le - 2\end{array} \right.\).
Cho mệnh đề sau: “Tứ giác \(ABCD\) là hình bình hành thì \(AB\parallel CD\)”. Phát biểu nào dưới đây là đúng?
Điều kiện cần để tứ giác \(ABCD\) có \(AB\parallel CD\) là tứ giác \(ABCD\) là hình bình hành;
Điều kiện đủ để tứ giác \(ABCD\) có \(AB\parallel CD\) là tứ giác \(ABCD\) là hình bình hành;
Tứ giác \(ABCD\) có \(AB\parallel CD\) là điều kiện cần và đủ để tứ giác \(ABCD\) là hình bình hành;
Tứ giác \(ABCD\) là hình bình hành là điều kiện cần để \(AB\parallel CD\).
Biểu diễn tập hợp \(A = \left\{ {x \in \mathbb{R},|x|\, < 2} \right\}\) trên trục số ta được




Cho tập hợp \(A = \left\{ { - 1;\,\,0;\,\,3;\,\,5;\,\,7;\,\,9} \right\}\) và \(B = \left\{ { - 2;\,\,0;\,\,9} \right\}\). Phần tử thuộc tập \(A\backslash B\) là
\(0\);
\(8\);
\( - 2\);
\[3\].
Trong các câu sau, mệnh đề nào là mệnh đề chứa biến?
\(\exists x \in \mathbb{R},{x^2} = - 2\);
\( - \frac{1}{2}x + 3 = 0\);
\(\left| x \right| \ge 0\) với mọi giá trị thực của x;
\(\forall x \in {\mathbb{N}^ * },{x^2} + x > 0\).
Cho hai tập hợp \(X = \left\{ {2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,17} \right\}\) và \(Y = \left\{ {1;\,\,3;\,\,5;\,\,8;\,\,12;\,\,17} \right\}\). Số phần tử của tập hợp \(X \cap Y\) là
0;
1;
2;
3.
Trong các cặp số \(\left( {x;\,y} \right)\) sau đây, cặp nào là nghiệm của bất phương trình \[\left\{ \begin{array}{l} - 2x + y < 1\\x - y \ge 0\end{array} \right.\]?
\(\left( {1;\,\,5} \right)\);
\(\left( { - 1;\,\,3} \right)\);
\(\left( {0;\,\,1} \right)\);
\(\left( {1;\,\,1} \right)\).
Cho góc \(0^\circ \le \alpha \le 180^\circ \) thỏa mãn \(\tan \alpha = 4\). Giá trị của biểu thức \[A = \frac{{\sin \alpha + \cos \alpha }}{{\sin \alpha - 3\cos \alpha }}\] là
\(A = 1\);
\(A = \frac{1}{2}\);
\(A = \frac{1}{5}\);
\(A = 5\).
Trong các đẳng thức sau, đẳng thức nào đúng với mọi góc \(\alpha \in \left( {0^\circ ;\,\,180^\circ } \right)\)?
\(\sin \left( {180^\circ - \alpha } \right) = \sin \alpha \);
\(\sin \left( {180^\circ - \alpha } \right) = c{\rm{os}}\alpha \);
\(\sin \left( {180^\circ - \alpha } \right) = - c{\rm{os}}\alpha \);
\(\sin \left( {180^\circ - \alpha } \right) = - {\rm{sin}}\alpha \).
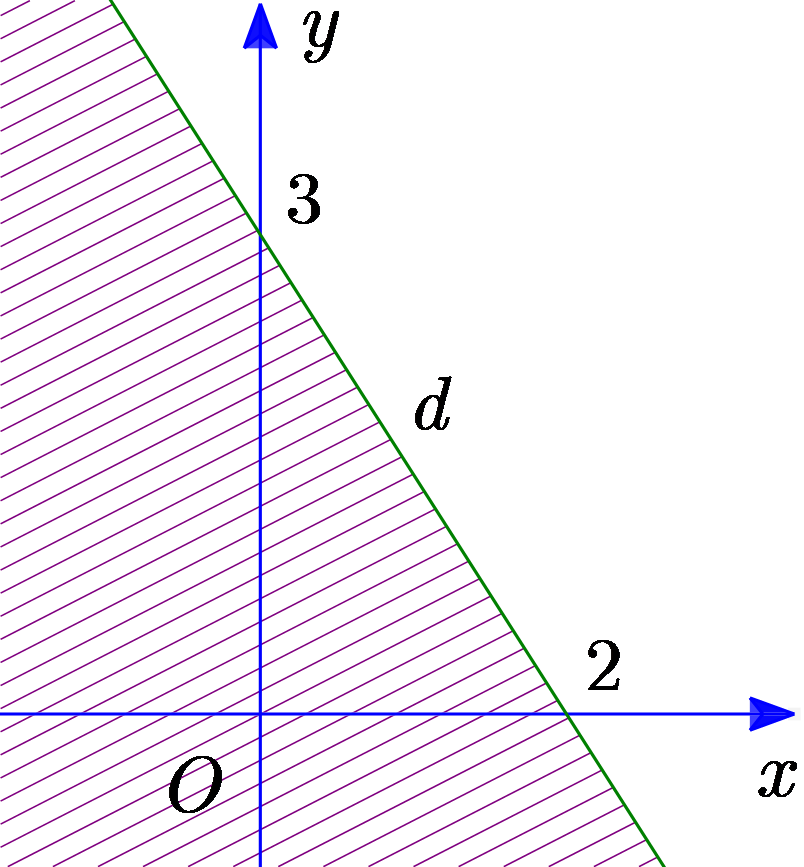
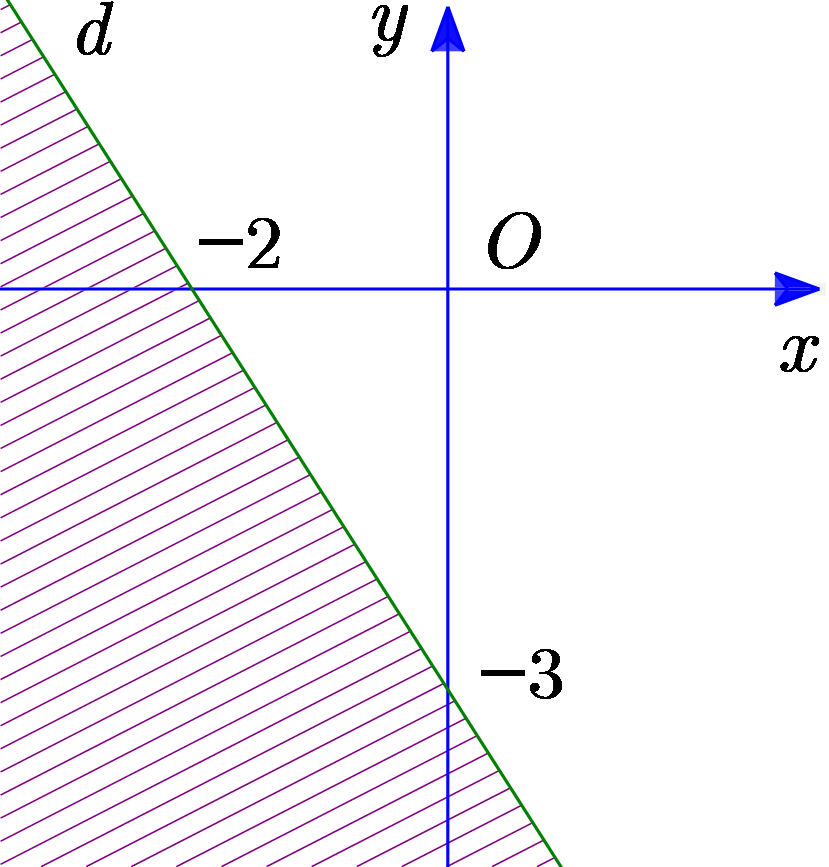
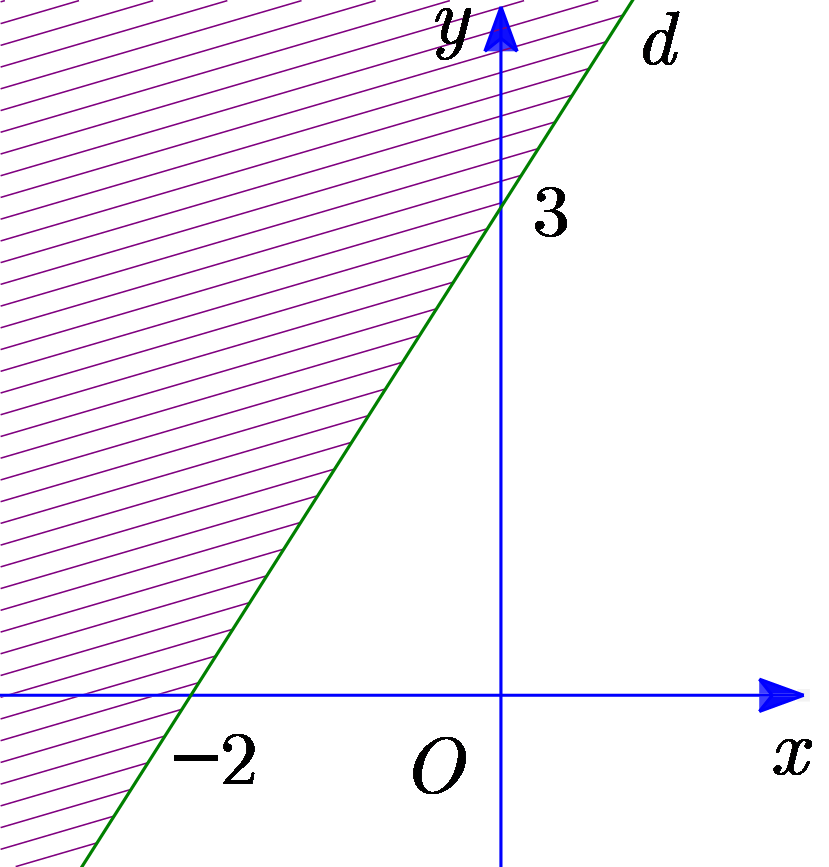
Miền nghiệm của bất phương trình \(3x - 2y > - 6\) được biểu diễn bởi phần không gạch chéo trong hình nào được cho dưới đây?
Cho tập hợp \(M = \left\{ {m;\,\,n;\,\,1;\,\,5} \right\}\). Số tập con của tập hợp M luôn chứa hai phần tử m và n là
\(16\);
\(8\);
\(4\);
\(3\).
Bất phương trình \(x + y \le 3\) có bao nhiêu nghiệm?
\(1\);
\(2\);
Vô nghiệm;
Vô số nghiệm.
Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào sau đây là đúng?
\(\sin A = 0\);
\(\sin A = c{\rm{os}}\left( {B + C} \right)\);
\(\sin A = - c{\rm{os}}\left( {B + C} \right)\);
\(\sin A = {\rm{sin}}\left( {B + C} \right)\).
Cho tam giác \(ABC\). Điểm \(K,\,\,M,\,\,N\) lần lượt là trung điểm của đoạn thẳng \(AB,\,\,BC\) và \(AC\). Vectơ nào sau đây cùng phương với \(\overrightarrow {KN} \)?
\(\overrightarrow {CB} \);
\(\overrightarrow {AC} \);
\(\overrightarrow {MN} \);
\(\overrightarrow {BN} \).
Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc \(50^\circ 35'\). Tàu thứ nhất chạy với tốc độ \(25\) km/h, tàu thứ hai chạy với tốc độ \(35\) km/h. Hỏi sau \(1,2\) giờ hai tàu cách nhau bao nhiêu km?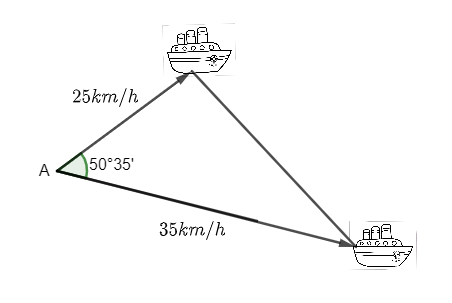
\(27,18\);
\(32,62\);
\(54,36\);
\(63,91\).
Cho tam giác \(ABC\) có \(R,r\) lần lượt là bán kính đường tròn ngoại tiếp, đường tròn nội tiếp tam giác \(ABC\), \(S\) là diện tích tam giác \(ABC\) và \(p\) là nửa chu vi tam giác \(ABC\). Công thức tính bán kính ngoại tiếp đường tròn ngoại tiếp tam giác \(ABC\) nào sau đây sai?
\(\frac{a}{{2\sin A}}\);
\(\frac{{2b}}{{\sin B}}\);
\(\frac{{abc}}{{4pr}}\);
\(\frac{{abc}}{{4S}}\).
Cho ba điểm A, B, C. Mệnh đề nào sau đây là đúng?
\(\overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CA} \);
\(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {BC} \);
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \);
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \).
Khẳng định nào sai trong các khẳng định sau?
Vectơ là một đoạn thẳng có hướng;
Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau;
Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài;
Hai vectơ cùng phương thì có giá song song với nhau.
Vectơ tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \) bằng
\(\overrightarrow {MN} \);
\(\overrightarrow {RN} \);
\(\overrightarrow {MR} \);
\(\overrightarrow {NP} \).
Phát biểu nào dưới đây là sai?
\(\left\{ {2\,\,007;2\,\,022} \right\} \subset \left[ {2\,\,007;2\,\,022} \right]\);
\(\emptyset \subset \mathbb{Z}\);
\(\mathbb{N} \subset \left[ {0;\,\, + \infty } \right)\);
\(\left[ {2;\,\,6} \right] = \left\{ {2;3;4;5;6} \right\}\).
II. TỰ LUẬN (3 ĐIỂM)
(1,0 điểm)
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}| - 1 < x \le 4} \right\}\).
a) Xác định phần bù của tập A trong tập hợp số thực.
b) Cho tập hợp \(B = \left[ { - 10;m - 2} \right]\). Tìm m để \(A \cap B \ne \emptyset \).
(1,0 điểm) Thời gian (tính bằng giờ) cần thiết để lắp ráp và đóng gói hai loại sản phẩm A và B được thể hiện trong bảng dưới đây.
Quy trình | Sản phẩm A | Sản phẩm B |
Lắp ráp | 3 | 3 |
Đóng gói | 1 | 2 |
Tổng số thời gian để lắp ráp và đóng gói sản phẩm lần lượt không quá 360 giờ, 200 giờ. Lợi nhuận khi bán sản phẩm A là 2 triệu đồng, sản phẩm B là 3 triệu đồng. Cần sản xuất bao nhiêu sản phẩm mỗi loại để lợi nhuận thu được là lớn nhất.
(1,0 điểm) Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \) và \(AB = AC = a\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(BM = \frac{{2BC}}{5}\). Tính độ dài \(AM\) và bán kính đường tròn nội tiếp tam giác \(ABM\).








