Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 09
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tập hợp \[A = \left\{ {\left. {{n^2} + 1} \right|n \in \mathbb{N},\,\,n \le 6} \right\}\]. Tập hợp nào sau đây là tập con của \(A\)?
\(\left\{ {\,1\,;\,3\,;\,5\,;\,7} \right\}\).
\(\left\{ {\,2\,;\,10\,;\,17\,;\,37} \right\}\).
\(\left\{ {\,5\,;\,7\,;\,9\,;\,37} \right\}\).
Cặp số nào sau đây không là nghiệm của bất phương trình \[x + 2y - 3 > 0\].
\(\left( { - 1;4} \right)\).
\(\left( { - 2;3} \right)\).
\(\left( {4;0} \right)\).
\(\left( { - 1;0} \right)\).
Trong các mệnh đề, mệnh đề nào sai?
\(\forall x \in \mathbb{R},{x^2} + 1 > 0.\)
\(\exists x \in \mathbb{R},{x^2} - 3x + 2 = 0.\)
\(\forall x \in \mathbb{R},\left| {x + 1} \right| \ge 0.\)
\(\exists x \in \mathbb{R},{x^2} < 0.\)
Điểm \[O\left( {0;0} \right)\] thuộc miền nghiệm của hệ bất phương trình nào sau đây?
\[\left\{ \begin{array}{l}x + 3y - 6 > 0\\2x + y + 4 > 0\end{array} \right.\].
\[\left\{ \begin{array}{l}x + 3y - 6 < 0\\2x + y + 4 > 0\end{array} \right.\].
\[\left\{ \begin{array}{l}x + 3y - 6 > 0\\2x + y + 4 < 0\end{array} \right.\].
\[\left\{ \begin{array}{l}x + 3y - 6 < 0\\2x + y + 4 < 0\end{array} \right.\].
Cho \[A = \left\{ {1;3;4;5;6;8;0} \right\}\] và \[B = \left\{ {1;3;4;5;6;9} \right\}\]. Khẳng định nào sau đây là đúng?
\[0 \in A\].
\[B \subset A\].
\[A \subset B\].
\[0 \in B\].
Cho tập \(A = \left[ {1;7} \right)\), , \(C = \left( {0; + \infty } \right)\). Tập \(A \cap B \cap C\) bằng\(B = \left( { - 2;5} \right]\)
\(\left( {0;7} \right)\).
\(\left( {1;5} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left[ {1;5} \right]\).
Giá trị nhỏ nhất của biểu thức trên miền xác định bởi hệ
Không tồn tại giá trị nhỏ nhất của \(F\).
\(\min F = 2\,khi\,x = 0,\,\,y = 2\).
\(\min F = 1\,khi\,x = 2,\,\,y = 3\)
\(\min F = 3\,khi\,x = 1,\,\,y = 4\).
Đường thẳng d: 2x - y = 2 chia mặt phẳng tọa độ thành hai miền I, II có bờ là đường thẳng d (như hình vẽ bên). Xác định miền nghiệm của bất phương trình 2.x - y 2.
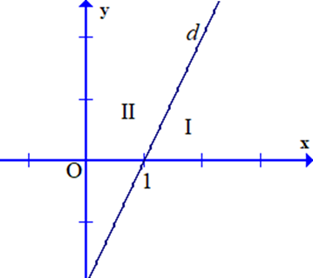
Nửa mặt phẳng I kể cả bờ d.
Nửa mặt phẳng II bỏ đi đường thẳng d.
Nửa mặt phẳng I bỏ đi đường thẳng d
Nửa mặt phẳng II kể cả bờ d.
Cho \(\sin \alpha = \frac{1}{{\sqrt 3 }}\) và \(\frac{\pi }{2} < \alpha < \pi \). Hãy tính \(\cos \alpha \)
\( - \frac{{\sqrt 6 }}{3}\).
\(\frac{{\sqrt 6 }}{2}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\sqrt 6 - \frac{1}{2}\).
Giá trị của biểu thức: \(\left( {2\sin {{30}^0} + {\rm{cos13}}{{\rm{5}}^0} - 3\tan {{150}^0}} \right)\left( {{\rm{cos}}{{180}^0} - {\rm{cos}}{{60}^0}} \right)\) là
\(\frac{1}{2}\).
\(\frac{{\sqrt 2 - 2\sqrt 3 }}{2}\).
\(\frac{{\sqrt 2 + 2\sqrt 3 }}{2}\).
\( - \frac{3}{2}\left( {1 - \frac{{\sqrt 2 - 2\sqrt 3 }}{2}} \right)\).
Tam giác \[ABC\] có\[BC = 12\],\[CA = 9\],\[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho\[BM = 4\]. Tính độ dài đoạn thẳng \[AM\]
\(2\sqrt 5 \).
\(3\sqrt 2 \).
\(\sqrt {20} \).
\(\sqrt {19} \).
Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1m, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?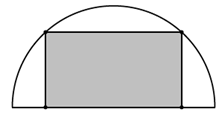
\[0,8\;{{\rm{m}}^2}\].
\[1,6\;{{\rm{m}}^2}\].
\[1\;{{\rm{m}}^2}\].
\[2\;{{\rm{m}}^2}\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một xưởng sản xuất hai loại sản phẩm như sau: Mỗi kg sản phẩm loại I cần \(2\) kg nguyên liệu và \(30\) giờ, mức lời \(40\) nghìn. Mỗi kg sản phẩm loại II cần \(4\) kg nguyên liệu và \(15\) giờ, mức lời \(30\) nghìn. Xưởng có \(200\) kg nguyên liệu và \(1200\) giờ làm việc.
a) Miền nghiệm của hệ bất phương trình là miền tứ giác \(OABC\) với \(O(0;0)\), \(A(0;40)\), \(B(20;45)\), \(C(40;0)\) kể cả cạnh của tứ giác.
b) Gọi \(x\), \(y\) lần lượt là số kg sản phẩm loại I và sản phẩm loại II, ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{y \ge 0}\\{2x + 4y \le 200}\\{30x + 15y \le 1200}\end{array}} \right.\).
c) Lợi nhuận bán sản phẩm \(F = 40x + 30y\) đạt GTLN tại điểm \(B(20;40)\).
d) Lợi nhuận lớn nhất thu được khi sản xuất \(40\) sản phẩm loại I và \(30\) sản phẩm loại II.
Cho các tập hợp . Xét tính đúng sai của các khẳng định sau:
a) \(H \subset G\) b) \(H = \left[ {0;17} \right]\) c) \(G \subset H\) d) \(G = \left[ { - 12\,;\,21} \right]\)
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời từ câu 1 đến câu 4.
Trên sườn đồi, với độ dốc .\(12\% \) (độ dốc của sườn đồi được tính bằng tang của góc nhọn tạo bởi sườn đồi với phương nằm ngang) có một cây cao mọc thẳng đứng. Ở phía chân đồi, cách gốc cây \(30\;m\), người ta nhìn ngọn cây dưới một góc \({45^^\circ }\) so với phương nằm ngang. Tính chiều cao của cây đó (làm tròn đến hàng đơn vị, theo đơn vị mét).
Lớp 10A1 có 40 học sinh, trong đó có 20 học sinh thích môn Ngữ Văn, 18 học sinh thích môn Toán, 4 học sinh thích cả hai môn Ngữ Văn và Toán. Hỏi có bao nhiêu học sinh không thích môn nào trong hai môn Ngữ Văn và Toán?
Cho hai tập hợp \(A = [m + 1;2m - 1],B = (0;6)\). Có bao nhiêu giá trị \(m\) nguyên để \(A \subset B\)?
Một người dùng ba loại nguyên liệu \(A,B,C\) để sản xuất ra hai loại sản phẩm \(P\) và \(Q\). Để sản xuất \(1\;kg\) mỗi loại sản phẩm \(P\) hoặc \(Q\) phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho trong bảng sau:
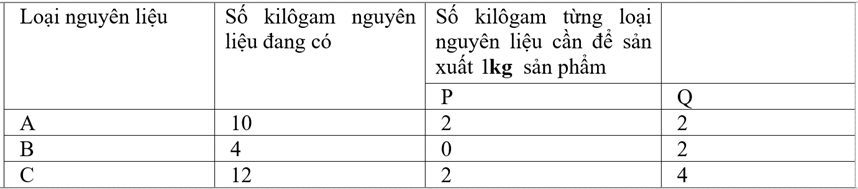
Biết \(1\;kg\) sản phẩm \(P\) có lợi nhuận 3 triệu đồng và \(1\;kg\) sản phẩm \(Q\) có lợi nhuận 5 triệu đồng. Người đó đã lập được phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Hỏi lãi cao nhất bằng bao nhiêu?
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Từ hai vị trí \(A\),\(B\) người ta quan sát một cái cây (hình vẽ). Lấy \(C\) là điểm gốc cây, \(D\) là điểm ngọn cây. \(A\),\(B\) cùng thẳng hàng với điểm \(H\) thuộc chiều cao \(CD\) của cây. Người ta đo được\(AB = 10m\), \(HC = 1,7m\), \(\alpha = 63^\circ \), \(\beta = 48^\circ \). Tính chiều cao của cây đó.
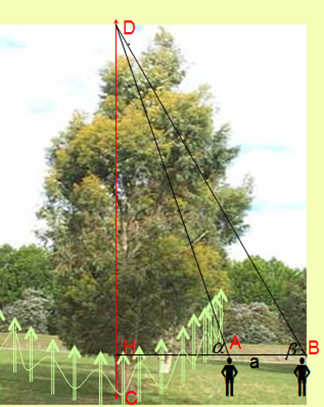
Gia đình chị Minh dự định trồng rau và hoa trên một mảnh đất có diện tích \(8\) ha\(4\). Nếu trồng \(1\) ha rau thì cần \(20\) ngày công và thu lợi \(3\) triệu đồng. Nếu trồng \(1\) ha hoa thì cần \(30\) ngày công và thu lợi triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá \(180\) ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng?
Cho góc \(x\) là góc nhọn và thỏa mãn \(\sin x = \frac{5}{6}\). Tính giá trị biểu thức \(P = - \cos x + \sin x\).








