Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 08
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Xác định số phần tử của tập hợp \(X = \left\{ {n \in \mathbb{N}|n\, \vdots \,4\,,\,n < 2017} \right\}\).
\(505\).
\(503\).
\(504\).
\(502\).
Cho \[A = \left\{ {1;3;4;5;6;8;9} \right\}\] và \[B = \left\{ {1;3;4;5;6;9} \right\}\]. Khẳng định nào sau đây là đúng?
\[B \subset A\].
\[0 \in A\].
\[A \subset B\].
\[0 \in B\].
Cho mệnh đề chứa biến \[P\left( n \right):\] "\[{n^2} - 1\] chia hết cho \[4\]" với \[n\] là số nguyên. Khẳng định nào sau đây đúng?
\[P\left( 5 \right)\] sai và \[P\left( 2 \right)\] sai.
\[P\left( 5 \right)\] sai và \[P\left( 2 \right)\] đúng.
\[P\left( 5 \right)\] đúng và \[P\left( 2 \right)\] đúng.
\[P\left( 5 \right)\] đúng và \[P\left( 2 \right)\] sai.
Điểm \(A\left( { - 1;3} \right)\) là điểm không thuộc miền nghiệm của bất phương trình nào sau đây?
\(3x - y \le 0\).
\(2x - y + 4 < 0\).
\( - 3x + 2y - 4 < 0\).
\(x + 3y > 0\).
Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - y > 0\\x - 3y \le - 3\\x + y > 5\end{array} \right.\] không chứa điểm nào sau đây?
\(B\left( {6\,\,;\,\,3} \right).\)
\(D\left( {5\,\,;\,\,4} \right).\)
\[A\left( {3\,\,;\,\,2} \right).\]
\(C\left( {6\,\,;\,\,4} \right).\)
Cho các tập hợp \(A = \left\{ {2;3;4;5;6;8} \right\},B = \left\{ {0;2;3;5;7} \right\}\). Có bao nhiêu tập \[X\] thỏa mãn \(X \subset A,X \subset B\)?
\(8\).
\(4\).
\(6\).
\(16\).
Cho \[\tan x = 2\], giá trị của biểu thức \[A = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 3\cos x}}{{4\sin x + 2\cos x}}\]là
\(\frac{8}{7}\).
\(2\).
\(\frac{7}{8}\).
\(\frac{1}{2}\).
Cho \(a;\,b;\,c\) là độ dài \(3\) cạnh của tam giác \(ABC\). Biết \(b = 7\);\(c = 5\);\(\cos A = \frac{4}{5}\). Tính độ dài của \(a\).
\(\frac{{23}}{8}\).
\(\frac{{7\sqrt 2 }}{2}\).
\(6\).
\(3\sqrt 2 \).
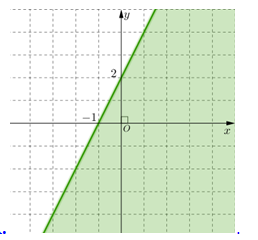
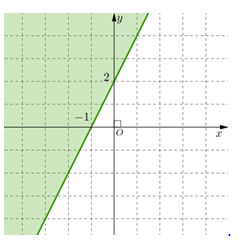
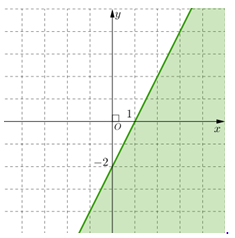
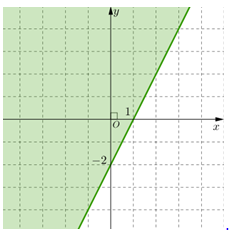
Miền nghiệm của bất phương trình \(2x - y \le - 2\) là
Giá trị lớn nhất của biểu thức \(F\left( {x;y} \right) = x + 2y\), với điều kiện \(\left\{ \begin{array}{l}0 \le y \le 4\\x \ge 0\\x - y - 1 \le 0\\x + 2y - 10 \le 0\end{array} \right.\) là
\(10\).
\(6\).
\(8\).
\(12\).
Biết \(\sin \alpha = \frac{2}{3}\left( {90^\circ < \alpha < 180^\circ } \right)\). Hỏi giá trị của \(\tan \alpha \)bằng bao nhiêu?
\(\frac{{2\sqrt 5 }}{5}\).
\( - \frac{{2\sqrt 5 }}{5}\).
\(2\).
\( - 2\).
Với các số đo trên hình vẽ sau, chiều cao \(h\) của tháp nghiêng Pisa gần giá trị nào nhất?
\(6.5\).
\(8\)
\(7\).
\(7.5\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hai nửa khoảng \(A = ( - \infty ;m],B = [5; + \infty )\).Vậy:
a) Nếu \(m > 5\) thì \(A \cap B = [5;m]\). b) Nếu \(m = 5\) thì \(A \cap B = \{ 5\} \).
c) Nếu \(m = 9\) thì \(A \cup B = ( - \infty ; + \infty )\). d) Nếu \(m < 5\) thì \(A \cap B = \emptyset \).
Một công ty TNHH trong một đợt quảng cáo và bán hàng khuyến mại hàng hóa (một sản phẩm mới của công ty) cần thuê xe để chở \(140\) người và \(9\) tấn hàng. Nơi thuê chỉ có hai loại xe \(A\) và \(B\). Trong đó xe loại \(A\) có \(10\) chiếc, xe loại \(B\) có \(9\) chiếc. Một chiếc xe loại \(A\) cho thuê với giá \(4\) triệu, loại \(B\) giá \(3\) triệu. Biết rằng xe \(A\) chỉ chở tối đa \(20\) người và \(0,6\) tấn hàng; xe \(B\) chở tối đa \(10\) người và \(1,5\) tấn hàng. Gọi \(x,y\) lần lượt là số xe loại \(A\) và loại \(B\) mà công ty thuê.
a) Số tiền thuê xe thấp nhất là \(32\) triệu.
b) \(2x + y < 14\).
c) \(2x + 5y \ge 30\).
d) Số tiền thuê xe là \(4x + 3y\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời từ câu 1 đến câu 4.
Một nhà máy sản xuất hai loại thức ăn gia súc: loại A và loại B; Để sản xuất 1 tấn thức ăn loại A cần 3 tấn nguyên liệu X, 2 tấn nguyên liệu Y và 1 tấn phụ gia. Để sản xuất 1 tấn thức ăn loại B cần 2 tấn nguyên liệu X, 4 tấn nguyên liệu Y và 3 tấn phụ gia. Nhà máy có tối đa 120 tấn nguyên liệu X, 160 tấn nguyên liệu Y và 80 tấn phụ gia. Biết rằng lợi nhuận thu được từ mỗi tấn thức ăn loại A là 20 triệu đồng và từ loại B là 30 triệu đồng. Lợi nhuận (đơn vị: triệu đồng) nhà máy thu được lớn nhất là bao nhiêu? (kết quả làm tròn đến hàng đơn vị)
Cho hai tập hợp \(A = (m - 1;5)\) và \(B = (3; + \infty )\). Biết rằng \(\left[ {a;b} \right)\)là tập tất cả các giá trị thực của tham số \(m\) để \(A\backslash B = \emptyset \). Tính \(b - a\).
Một người đứng ở vị trí \(A\) trên nóc một ngôi nhà cao \(4\;m\) đang quan sát một cây cao cách ngôi nhà \(20\;m\) và đo được \(\widehat {BAC} = {45^^\circ }\). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).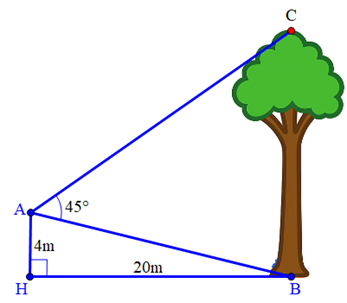
Cho tập \(M\) có 100 số tự nhiên mà mỗi số hoặc chia hết cho 5 hoặc chia hết cho 7 hoặc chia hết cho cả 5 và 7. Biết rằng trong số đó có 71 số chia hết cho 5 và 63 số chia hết cho 7. Hỏi tập \(M\) có bao nhiêu số chia hết cho 35 ?
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Cho hệ bất phương trình sau: \(\left\{ {\begin{array}{*{20}{l}}{2x - 1 \ge 0}\\{ - y + 1 \le 0}\end{array}} \right.\). Gọi \(\left( {{x_0};{y_0}} \right)\) là một nghiệm của hệ trên. Tìm giá trị nhỏ nhất của \(3{x_0} + {y_0}\).
Cho \({0^ \circ } \le x \le {180^0}\) và \(\cos x = \frac{{\sqrt 6 + \sqrt 2 }}{4}\), tính \(P = 3\sin x + \cos x\)
Trong một lần đi khảo sát các đảo thuộc quần đảo Trường Sa của Việt Nam, các nhà khoa học phát hiện có một đảo có dạng hình tròn, tâm của đảo này bị che bởi một bãi đá nhỏ mà các nhà khoa học không thể tới được. Các nhà khoa học muốn đo bán kính của đảo này, biết rằng các nhà khoa học chỉ có dụng cụ là thước thẳng dài. Nêu cách để các nhà khoa học tính được bán kính đảo?








