Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 06
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Miền nghiệm của bất phương trình \[x + 3y - 2 < 0\] là nửa mặt phẳng chứa điểm nào trong các điểm sau:
\[A\left( {1;\,1} \right)\].
\[C\left( {0;\,1} \right)\].
\[B\left( { - 1;\,0} \right)\].
\[D\left( {2;\,1} \right)\].
Cặp số \[\left( {x;y} \right) = \left( {19;8} \right)\] là một nghiệm của bất phương trình nào sau đây?
\[x - 2y + 1 \ge 0\].
\[x--y < 0\].
\(3x - y - 5 < 0\).
\[2x - 5y--1 > 0\].
Hãy liệt kê các phần tử của tập hợp \[X = \left\{ {x \in \mathbb{R}|{x^2} + x + 1 = 0} \right\}\].
\[X = \left\{ \emptyset \right\}\].
\[X = 0\].
\[X = \emptyset \].
\[X = \left\{ 0 \right\}\].
Cho tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}} \right|{x^2} - 6x + 8 = 0} \right\}\). Hãy viết lại tập hợp \(A\) bằng cách liệt kê các phần tử.
\(A = \emptyset \).
\(A = \left\{ { - 2\,;4} \right\}\).
\(A = \left\{ {2\,;4} \right\}\).
\(A = \left\{ { - 4\,; - 2} \right\}\).
Cho định lý “Nếu hai tam giác bằng nhau thì diện tích bằng nhau”. Mệnh đề nào sau đây đúng?
Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.
Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.
Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.
Đường thẳng \(d:2x - y = 2\) chia mặt phẳng tọa độ thành hai miền I, II có bờ là đường thẳng \(d\) (hình vẽ bên). Xác định miền nghiệm của bất phương trình \(2x - y > 2\).
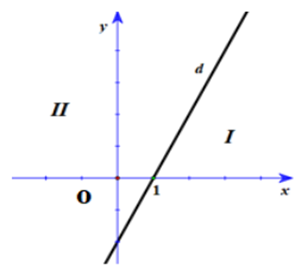
Nửa mặt phẳng I bỏ đi đường thẳng \(d\).
Nửa mặt phẳng II kể cả bờ \(d\).
Nửa mặt phẳng I kể cả bờ \(d\).
Nửa mặt phẳng II bỏ đi đường thẳng \(d\).
Biết \(\tan \alpha = - 3,\left( {{0^0} \le \alpha \le {{180}^0}} \right).\) Khi đó giá trị của \(\cos \alpha \) là
\( \pm \frac{{\sqrt {10} }}{{10}}\).
\( - \frac{{\sqrt {10} }}{{10}}\).
\(\frac{{\sqrt {10} }}{{10}}\) .
\(\frac{1}{{10}}\).
Cho ba tập hợp \[X = \left( { - 4;3} \right)\] và \(Y = \left\{ {\left. {x \in \mathbb{R}} \right|2x + 4 > 0,\,x < 5} \right\}\) và \(Z = \left\{ {\left. {x \in \mathbb{R}} \right|\left( {x + 3} \right)\left( {x - 4} \right) = 0} \right\}\). Hãy chọn mệnh đề đúng ?
\(X \subset Y\).
\(Z \subset X\).
\(Z \subset X \cup Y\).
\(Z \subset Y\).
Cho \(\tan x = 3\). Giá trị biểu thức \(T = \frac{{\sin x + \cos x}}{{2\cos x + \sin x}}\) bằng
\(T = - \frac{7}{{16}}\) .
\(T = \frac{4}{5}\).
\(T = - \frac{4}{5}\).
\(T = \frac{7}{{16}}\).
Giá trị nhỏ nhất của biểu thức \[F\left( {x;y} \right) = x - 2y\], với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 5}\\{x \ge 0}\\{x + y - 2 \ge 0}\\{x - y - 2 \le 0}\end{array}} \right.\) là
\( - 12\).
\[ - 10\].
\[ - 6\].
\[ - 8\].
Cho tam giác \[ABC\] có \[AB = 2,AC = 1\] và \[\widehat {A{\rm{ }}} = 60^\circ \]. Độ dài cạnh \[BC\] bằng
\[BC = 1\].
\[BC = \sqrt 2 \].
\[BC = \sqrt 3 \].
\[BC = 2\].
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh thuận người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3m.\) Gọi \(D\) là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao \(CD\) của tháp. Người ta đo được góc \(\widehat {D{A_1}{C_1}} = {49^o}\) và \(\widehat {D{B_1}{C_1}} = {35^o}.\) Tính chiều cao \(CD\) của tháp.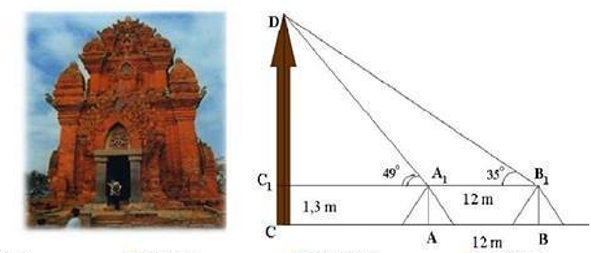
\(21,47m\).
\(20,47m\).
\(22,77m\).
\(21,77m\).
PHẦN II. Câu trắc nghiệm đúng sai.Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Lớp 10C6 có 18 học sinh tham gia câu lạc bộ bóng đá và 15 học sinh tham gia câu lạc bộ bóng rổ. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên. Khi đó:
a) Có 9 học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ.
b) Có 22 học sinh tham gia ít nhất một trong hai câu lạc bộ trên.
c) Biết lớp \(10C6\) có 45 học sinh. Có 22 học sinh không tham gia cả hai câu lạc bộ.
d) Biết lớp \(10C6\) có 45 học sinh. Có 25 học sinh không tham gia câu lạc bộ bóng đá.
Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y \ge 9}\\{x - 2y \le 3}\\{x + y \le 6}\\{x \ge 1}\end{array}} \right.({\rm{I}})\). Khi đó
a) \(x = 1\); \(y = 5\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị nhỏ nhất.
b) Miền nghiệm của hệ bất phương trình là miền tam giác.
c) \((3;2)\)là một nghiệm của hệ bất phương trình.
d) \(x = 1\); \(y = 3\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị lớn nhất.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Một \(10C14\) có 45 học sinh chuẩn bị cho hội diễn văn nghệ chào mừng ngày nhà giáo Việt Nam 20/11. Trong danh sách đăng kí tham gia tiết mục nhảy Flashmob và tiết mục hát, có 35 học sinh tham gia tiết mục nhảy Flashmob, 10 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong lớp tham gia tiết mục hát? Biết rằng lớp \(10C14\) có bạn Kiệt, Hạ, Toàn, Thiện bị khuyết tật hòa nhập nên không tham gia tiết mục nào, các bạn còn lại tham gia ít nhất một tiết mục.
Cho hai tập hợp \(A = (m;m + 1)\) và \(B = [ - 1;3]\). Có bao nhiêu giá trị nguyên của \(m\) trong khoảng \(\left( {0;100} \right)\) để \(A \cap B = \emptyset \).
Một xưởng sản xuất đồ gỗ mỹ nghệ sản xuất ra hai loại sản phẩm I và II. Mỗi bộ sản phẩm loại I lãi 4 triệu đồng, mỗi bộ sản phẩm loại II lãi 5 triệu đồng. Để sản xuất mỗi bộ sản phẩm loại I cần máy làm việc trong \(3\) giờ và nhân công làm việc trong 1 giờ. Để sản xuất mỗi bộ sản phẩm loại II cần máy làm việc trong 4 giờ và nhân công làm việc trong 2 giờ. Biết rằng chỉ dùng máy hoặc chỉ dùng nhân công không thể đồng thời làm hai loại sản phẩm cùng lúc, số nhân công luôn ổn định. Một ngày máy làm việc không quá 18 giờ, nhân công làm việc không quá 8 giờ. Hỏi một ngày tiền lãi lớn nhất là bao nhiêu triệu đồng?
Từ một tấm tôn hình tròn có bán kính \(R = 1\;m\), bạn Trí muốn cắt ra một hình tam giác \(ABC\) có các góc \(A = {45^^\circ },B = {75^^\circ }\). Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung \(AB,BC\) có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?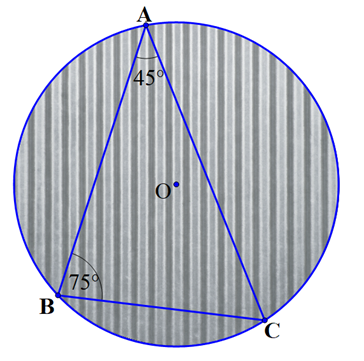
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
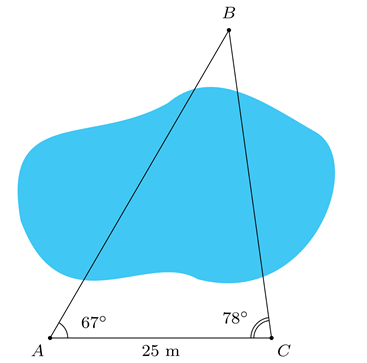
Để đo khoảng cách từ vị trí \(A\) đến vị trí \(B\) ở hai bên bờ một cái ao, bạn Cúc đi dọc bờ ao từ vị trí \(A\) đến vị trí \(C\) và tiến hành đo các góc \(BAC\), \(BCA\). Biết \(AC = 25m\), \(\widehat {BAC} = {67^^\circ }\), \(\widehat {BCA} = {78^^\circ }\) (hình vẽ bên). Hỏi khoảng cách từ vị trí \(A\) đến vị trí \(B\) là bao nhiêu mét?
Một gia đình cần ít nhất \(900\) đơn vị protein và \(200\) đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki-lô-gram thịt bò chứa \(800\) đơn vị protein và \(100\) đơn vị lipit. Mỗi ki-lô-gram thịt heo chứa \(500\) đơn vị protein và \(300\) đơn vị lipit. Biết cửa hàng bán thịt chỉ còn \(1,8\) kg thịt bò và \(1,2\) kg thịt heo. Giá \(1\) kg thịt bò là \(250\) nghìn đồng, \(1\) kg thịt heo là \(150\) nghìn đồng. Tính số tiền (đơn vị nghìn đồng) ít nhất mà gia đình đó cần dùng để mua thịt mà vẫn đảm bảo lượng protein là lipit trong thức ăn.
Cho góc \(a\) thỏa mãn \(\cos a = \frac{5}{7}\). Tính giá trị biểu thức \(P = \frac{{ - \cot a - 2\tan a}}{{4\cot a - 2\tan a}}\).








