Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 05
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề nào sau đây có mệnh đề đảo đúng?
Nếu hai góc đối đỉnh thì bằng nhau.
Nếu một số chia hết cho \[6\] thì cũng chia hết cho \[3\].
Nếu một phương trình bậc hai có \[\Delta < 0\] thì phương trình đó vô nghiệm.
Nếu \[a = b\] thì \[{a^2} = {b^2}\].
Cặp số \[\left( {x;y} \right) = \left( {9;8} \right)\] là một nghiệm của bất phương trình nào sau đây?
\[x--y < 0\].
\[2x - 5y--1 > 0\].
\(x + 3y - 5 < 0\).
\[2x - y + 1 \ge 0\].
Để viết mệnh đề “7 là số tự nhiên” ta dùng ký hiệu
\(7 \subset \mathbb{N}\).
\(7 < \mathbb{N}\).
\(7 \in \mathbb{N}\).
\(7 \le \mathbb{N}\).
Cho A là tập hợp. Xác định mệnh đề đúng trong các mệnh đề sau đây?
\[A \cup \emptyset = \emptyset \].
\[A \cap \emptyset = A\].
\[\emptyset \subset A\].
\[\left\{ \emptyset \right\} \subset A\].
Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\] chứa điểm nào sau đây?
\(D\left( {0\,\,;\,\, - \frac{1}{3}} \right).\)
\(A\left( {1\,\,;\,\,2} \right).\)
\(B\left( {0\,\,;\,\,2} \right)\).
\(C\left( { - 1\,\,;\,\,3} \right)\).
Cho \(\sin \alpha = \frac{1}{3}\)với \({90^0} < \alpha < {180^0}\). Giá trị của \(\cos \alpha \)bằng
\[ - \frac{{2\sqrt 2 }}{3}\].
\[\frac{2}{3}\].
\[\frac{{2\sqrt 2 }}{3}\].
\[ - \frac{2}{3}\].
Tam giác \[ABC\] vuông tại \[A\]có \[AB = AC = a\]. Điểm \[M\]nằm trên cạnh \[BC\]sao cho \(BM = \frac{{BC}}{3}\). Độ dài \[AM\]bằng bao nhiêu?
\(\frac{{2a}}{3}\).
\(\frac{{a\sqrt {17} }}{3}\)
\(\frac{{2a\sqrt 2 }}{3}\).
\(\frac{{a\sqrt 5 }}{3}\).
Hình dưới đây biểu diễn hình học miền nghiệm của bất phương trình nào? (Miền nghiệm là miền không gạch chéo và miền nghiệm không chứa đường thẳng)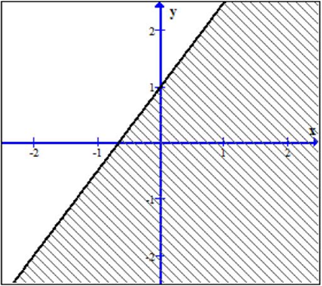
\[3x + 2y > 2\].
\[ - 3x + 2y > 2\].
\[3x + 2y < 2\].
\[ - 3x + 2y < 2\].
![]()
\(\left[ { - 3;4} \right)\).
\(\left[ {3; + \infty } \right)\).
\(\left( { - 2;4} \right)\).
\(\left[ { - 2;4} \right)\).
Cho tam giác đều \[ABC\]. Tính \(P = \cos (\overrightarrow {AB} ,\overrightarrow {BC} ) + \cos (\overrightarrow {BC} ,\overrightarrow {CA} ) + \cos (\overrightarrow {CA} ,\overrightarrow {AB} ).\)
\(P = \frac{{3\sqrt 3 }}{2}\).
\(P = - \frac{{3\sqrt 3 }}{2}\).
\(P = - \frac{3}{2}\).
\(P = \frac{3}{2}\).
Xét biểu thức \(F = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\). Chọn mệnh đề đúng.
\[\min F = 1\] khi \[x = 2,{\rm{ }}y = 3\].
\[\min F = 2\] khi \[x = 0,{\rm{ }}y = 2\].
\[\min F = 0\] khi \[x = 4,{\rm{ }}y = 4\].
\[\min F = 3\] khi \[x = 1,{\rm{ }}y = 4\].
Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB\) bằng \(70m\), phương nhìn \(AC\) tạo với phương nằm ngang góc \(30^\circ \). Phương nhìn \(BC\) tạo với phương nằm ngang góc \(15^\circ 30'\). Khi đó chiều cao của ngọn núi so với mặt đất (làm tròn đến hàng đơn vị) bằng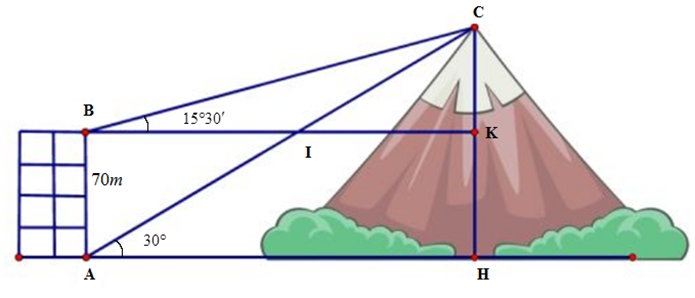
\(136m\).
\(135m\).
\(134m\).
\(133m\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Bác An dự định trồng hai loại cây ăn trái là mít và xoài trong nông trại rộng \(100\) (hecta). Biết mỗi hecta trồng mít cần \(20\) công chăm sóc và thu lại lợi nhuận \(150\) triệu đồng, mỗi hecta trồng xoài cần \(40\) công chăm sóc và thu lại lợi nhuận \(180\) triệu đồng. Biết rằng tổng số công cần dùng không được vượt quá \(2800\) công. Gọi \(x\), \(y\) (hecta) lần lượt là diện tích đất dùng để trồng mít và xoài.
a) \(x + 2y \le 140\).
b) \(x + y \le 100\).
c) Tổng lợi nhuận thu được là \(F = 150x + 180y\) triệu đồng.
d) Lợi nhuận thu được lớn nhất là \(16\) tỷ đồng.
Cho hai tập hợp \(A\) và \(B\) biết \(A\backslash B = \{ a;f\} ,A \cup B = \{ a;b;c;d;e;f;g;h\} \), \(B\backslash A = \{ b;g;h\} \). Vậy:
a) \(B = \{ b;c;d;e;g;h\} \)
b) \(A \cap B = \{ c;d;e\} .\)
c) \(A \subset B\)
d) \(A = \{ a;c;d;e;f\} \)
Một xưởng có máy cắt và máy tiện dùng để sản xuất trục sắt và đinh ốc. Sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu. Sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu. Một máy không thể sản xuất cả 2 loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Theo tính toán, nếu một ngày xưởng sản xuất được \(a\) tấn trục sắt và \(b\) tấn đinh ốc thì tiền lãi sẽ đạt cao nhất. Tính \(T = a + 3b\).
Cho hai tập \(A = ( - \infty ;m)\) và \(B = [2m - 2;2m + 2]\). Số nguyên \(m\) lớn nhất để \(\left( {{C_\mathbb{R}}A} \right) \cap B \ne \emptyset \) là số nào?
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (\(AB = 4,3\)cm;\(BC = 3,7\)cm; \(CA = 7,5\) cm). Tính bán kính của chiếc đĩa. (làm tròn kết quả đến hàng phần trăm)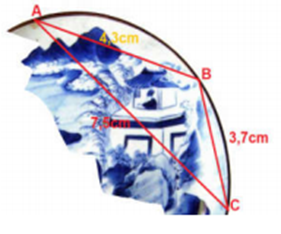
Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao?
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Biết rằng \(\sin {15^ \circ } = \frac{{\sqrt 6 - \sqrt 2 }}{4}\). Tính các giá trị lượng giác còn lại của góc \({15^ \circ }\). Chứng minh\(2\sin {15^ \circ }.\cos {15^ \circ } = \sin {30^ \circ }\)
Bạn Quân đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn Quân tới chiếc diều và phương nằm ngang) là \(\alpha = {28^^\circ }\); khoảng cách từ đỉnh tòa nhà tới mắt bạn Quân là \(1,1\)m. Cùng lúc đó ở dưới chân tòa nhà, bạn Nga cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {67^^\circ }\); khoảng cách từ mặt đất tới mắt bạn Nga cũng là \(1,1\)m. Biết chiều cao của tòa nhà là \(h = 26m\) (minh họa ở hình bên). Chiếc diều bay cao bao nhiêu mét so với mặt đất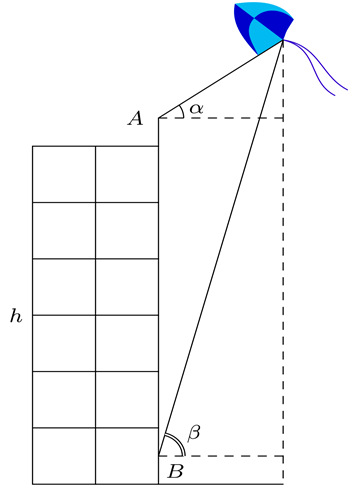
Một đại lý xe máy có kế hoạch nhập về hai dòng xe máy \(A\) và \(B\), giá mỗi chiếc lần lượt là \(40\) triệu đồng và \(60\) triệu đồng với số vốn ban đầu không vượt quá \(4,8\) tỉ đồng. Xe máy \(A\) mang lợi nhuận \(8\) triệu đồng cho mỗi chiếc và xe máy \(B\) mang lợi nhuận \(10\) triệu đồng cho mỗi chiếc. Đại lý ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá \(90\) chiếc cả hai loại. Chủ đại lý cần đầu tư kinh doanh \(a\) chiếc loại \(A\) và \(b\) chiếc loại \(B\) để thu được lợi nhuận lớn nhất. Tính \(a \cdot b\).








