Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 04

Miền nghiệm của bất phương trình\[3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\] là phần mặt phẳng chứa điểm nào?

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x > 0\\x - y \le 2\\x + y \le 1\end{array} \right.\) chứa điểm nào sau đây?

Cho \(S\) là mệnh đề “Nếu tổng các chữ số của một số \(n\) chia hết cho \(6\) thì \(n\) chia hết cho \(6\)”. Một giá trị của \(n\) để khẳng định \(S\) sai là

Cho tập \(A = \left\{ {0;1} \right\}\). Tập \(A\) có bao nhiêu tập con?

Miền nghiệm của bất phương trình \(3x - 2y >  - 6\) là

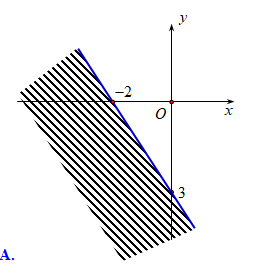
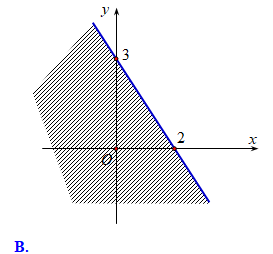
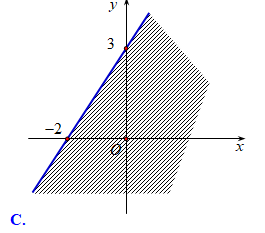
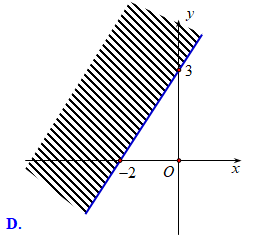
Cho \(\alpha \) là góc tù và \(\sin \alpha  = \frac{5}{{13}}\). Giá trị của biểu thức \(3\sin \alpha  + 2\cos \alpha \) là

Cho\(\sin \alpha  = \frac{1}{3}\) với \({90^0} < \alpha  < {180^0}\). Giá trị của \(\cos \alpha \) bằng

Cho tam giác\[ABC\] biết \[c = 5{\rm{cm}};\;b = 8{\rm{cm}},\widehat A = {60^0}\]. Bán kính đường tròn nội tiếp tam giác\[ABC\] bằng

Cho tập hợp \(A = \left( { - \infty ;m - 1} \right)\), \(B = \left[ {1; + \infty } \right)\). Tìm tất cả giá trị của \(m\) để \(A \cap B = \emptyset \) là

Biểu thức \(F = y - x\) đạt giá trị nhỏ nhất với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \le  - 2}\\{x - 2y \le 2}\\{x + y \le 5}\\{x \ge 0}\end{array}} \right.\)tại điểm \[S\left( {x;y} \right)\] có toạ độ là

Từ một đỉnh tháp chiều cao \(CD = 80{\rm{m}}\), người ta nhìn hai điểm \(A\) và \(B\) trên mặt đất dưới các góc \(72^\circ 12'\) và \(34^\circ 26'\). Ba điểm \(A,\;B,\,D\) thẳng hàng. Tính khoảng cách \(AB\).

PHẦN II. Câu trắc nghiệm đúng sai.Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

 Cho ba tập hợp \(A = \left\{ {2;5} \right\}\,;\,B = \left\{ {5;x} \right\}\,;\,C = \left\{ {x;y;5} \right\}\),biết \(A = B = C\). Xét tính đúng sai của các khẳng định sau:

a) \(x = y = 2\)thì \(A = B = C\)                                      

b) \(x = 1,y = 3\)thì \(A = B = C\)

c) \(x = y = 3\)thì \(A = B = C\)                                       

 d) \(x = 2,y = 5\)thì \(A = B = C\)

Bác Minh có kế hoạch đầu tư không quá \(240\) triệu đồng vào hai khoản \(X\) và khoản \(Y\). Để đạt được lợi nhuận thì khoản \(Y\) phải đầu tư ít nhất \(40\) triệu đồng và số tiền đầu tư cho khoản \(X\) phải ít nhất gấp ba lần số tiền cho khoản \(Y\). Khi đó

a) Điểm \(C(200;40)\) không thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.

b) Miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho là một tứ giác.

c) Điểm \(A(180;60)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.

d) Gọi \(x\), \(y\) (đơn vị: triệu đồng) tiền bác Minh đầu tư vào kho ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y.}\end{array}} \right.\).

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.

 Cho hai tập hợp \(A = \left[ {m - 3;\frac{{m + 2}}{4}} \right),B = ( - \infty ; - 1) \cup [2; + \infty )\). Có bao nhiêu giá trị nguyên của \(m\) để \(A \cap B = \emptyset \).

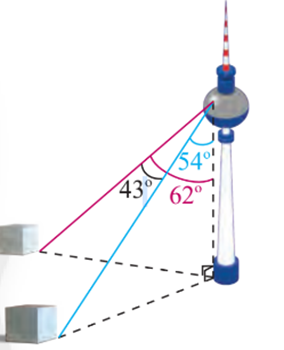
Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là ${43}^{°}$, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là ${62}^{°}$ và ${43}^{°}$đến điểm mốc khác là ${54}^{°}$ (Hình bên). Tính khoảng cách giữa hai cột mốc này(kết quả làm tròn đến hàng đơn vị)

Trong một nhóm gồm 40 khách du lịch có 27 du khách biết tiếng Anh, 21 du khách biết tiếng Pháp và 12 du khách biết cả hai thứ tiếng đó. Hỏi có bao nhiêu du khách không biết cả hai thứ tiếng đó?

Trong một cuộc thi pha chế đồ uống gồm hai loại là \(A\) và \(B\), mỗi đội chơi được sử dụng tối đa \(24\;g\) hương liệu, 9 cốc nước lọc và \(210\;g\) đường. Để pha chế 1 cốc đồ uống loại \(A\) cần 1 cốc nước lọc, \(30\;g\) đường và \(1\;g\) hương liệu. Để pha chế 1 cốc đồ uống loại \(B\) cần 1 cốc nước lọc, \(10\;g\) đường và \(4\;g\) hương liệu. Mỗi cốc đồ uống loại \(A\) nhận được 6 điểm thương, mỗi cốc đồ uống loại \(B\) nhận được 8 điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế bao nhiêu cốc đồ uống loại A?

PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.

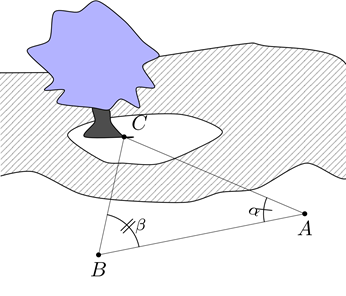
 Để đo khoảng cách từ một điểm \(A\) trên bờ sông đến gốc cây \(C\) trên cù lao giữa sông, người ta chọn một điểm \(B\) cùng ở trên bờ với \(A\) sao cho từ \(A\) và \(B\) có thể nhìn thấy điểm \(C\). Ta đo được khoảng cách \(AB = 66\) m, $\widehat{CAB}={39}^{°}$ và $\widehat{CBA}={69}^{°}$. Tính độ dài \(AC\)

Một cơ sở chiết xuất ít nhất \(140\) kg chất \(X\) và ít nhất \(18\) kg chất \(Y\) từ hai loại nguyên liệu loại I và loại II. Với mỗi tấn nguyên liệu loại I, người ta chiết xuất được \(20\) kg chất \(X\) và \(1,2\) kg chất \(Y\). Với mỗi tấn nguyên liệu loại II, người ta chiết xuất được \(10\) kg chất \(X\) và \(3\) kg chất \(Y\). Giá mỗi tấn nguyên liệu loại I là \(12\) triệu đồng và loại II là \(8\) triệu đồng. Hỏi người ta phải dùng ít nhất bao nhiêu triệu đồng để mua nguyên liệu mà vẫn đạt mục tiêu đề ra. Biết rằng cơ sở nhập nguyên liệu tối đa \(9\) tấn nguyên liệu loại I và tối đa \(8\) tấn nguyên liệu loại II. (Làm tròn kết quả đến hàng đơn vị).

Cho góc \(\beta \) thỏa mãn \(\sin \beta  = \frac{4}{5}\). Tính giá trị biểu thức \(P = \frac{{ - 2\cot \beta  + 2\tan \beta }}{{\cot \beta  - 4\tan \beta }}\).