Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 03
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Ký hiệu nào sau đây để chỉ 6 là số tự nhiên
\(6 \subset N\).
\(6 \notin N\).
\(6 = N\).
\(6 \in N\).
Cho định lý “Nếu hai tam giác bằng nhau thì hai tam giác có diện tích bằng nhau”. Mệnh đề nào sau đây đúng?
Hai tam giác bằng nhau là điều kiện cần để hai tam giác có diện tích bằng nhau.
Hai tam giác bằng nhau là điều kiện cần và đủ để hai tam giác có diện tích bằng nhau.
Hai tam giác có diện tích bằng nhau là điều kiện cần và đủ để hai tam giác có diện tích bằng nhau.
Hai tam giác bằng nhau là điều kiện đủ để hai tam giác có diện tích bằng nhau.
Cặp số nào sau đây là nghiệm của bất phương trình \[2x - y + 1 < 0\]?
\(\left( {3;5} \right)\).
\(\left( {2; - 1} \right)\).
\(\left( {1;4} \right)\).
\(\left( {0; - 1} \right)\)
Cho tập hợp \[A = \left\{ {a;b;c;d} \right\}\], phát biểu nào là sai?
\[\left\{ {a;d} \right\} \not\subset A\].
\[a \in A\].
\[\left\{ {b;c} \right\} \subset A\].
\[\left\{ d \right\} \subset A\].
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y + 2 > 0\\2x + y > 3\end{array} \right.\) là phần mặt phẳng chứa điểm
\(\left( { - 1;2} \right)\).
\(\left( {1;1} \right)\).
\(\left( {1;2} \right)\).
\(\left( {2; - 1} \right)\).
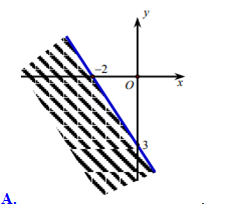
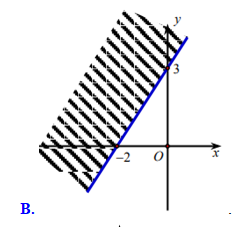
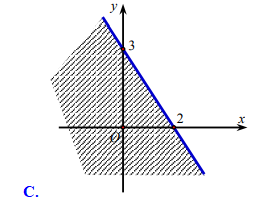
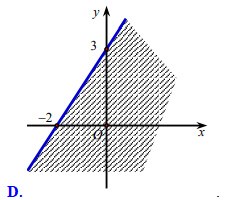
Miền nghiệm của bất phương trình \[3x - 2y < - 6\] là
Cho \[\cos x = \frac{1}{2}\]. Tính biểu thức \[P = 3{\sin ^2}x + 4{\cos ^2}x.\]
\[P = \frac{{11}}{4}.\]
\[P = \frac{{15}}{{14}}.\]
\[P = \frac{7}{4}.\]
\[P = \frac{{13}}{4}.\]
Cho tam giác \[ABC\] có \(AB = 4\), \(\widehat {ACB} = 45^\circ \) và \(\widehat {BAC} = 60^\circ \). Độ dài cạnh \(BC\)bằng
\(2\sqrt 6 \).
\(4\sqrt 6 \).
\[\frac{{4\sqrt 6 }}{3}\].
\[\frac{{8\sqrt 6 }}{3}\].
Biết\(\cot \alpha = - a,\) \(a > 0\) và \(0^\circ < \alpha < 180^\circ \). Tính \(\cos \alpha \).
\(\cos \alpha = \frac{a}{{\sqrt {1 + {a^2}} }}\).
\(\cos \alpha = \frac{1}{{\sqrt {1 + {a^2}} }}\).
\(\cos \alpha = - \frac{1}{{\sqrt {1 + {a^2}} }}\).
\(\cos \alpha = - \frac{a}{{\sqrt {1 + {a^2}} }}\).
Cho 2 tập hợp \[A = \left\{ {\left. {x \in \mathbb{R}} \right|(2x - {x^2})(x - 1) = 0} \right\}\], \[B = \left\{ {\left. {n \in \mathbb{N}} \right|0 < {n^2} < 10} \right\}\]. Chọn mệnh đề đúng?
\[A \cap B = \left\{ 2 \right\}\].
\[A \cap B = \left\{ {0\,;3} \right\}\].
\[A \cap B = \left\{ {0\,;\,1\,;\,2\,;\,3} \right\}\].
\[A \cap B = \left\{ {1\,;\,2} \right\}\].
Tìm giá trị nhỏ nhất của biết thức \(F = x - y\) biết \(x;y\) thỏa mãn điều kiện \[\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\], và biết hệ \[\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\] có miền nghiệm là phần tô đậm trong hình vẽ bên dưới.
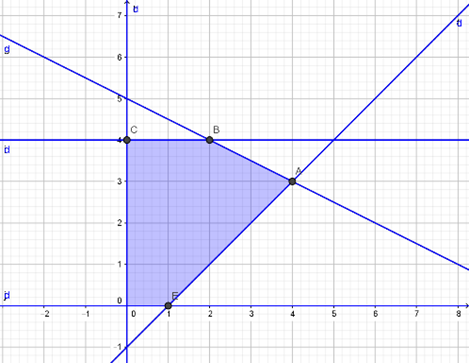
\(\min F = 0\).
\(\min F = - 7\).
\(\min F = 1\).
\(\min F = - 4\).
Từ hai vị trí \[A,\,\,B\] của một tòa nhà, người ta quan sát đỉnh \[C\] của một ngọn núi. Biết rằng \[A\] là điểm nằm phía chân của tòa nhà tiếp xúc với mặt đất, \[B\] là điểm nằm trên nóc của tòa nhà, phương \[A\,B\] vuông góc với mặt đất, khoảng cách \[A\,B\] là 70\[(m)\], phương nhìn \[AC\] tạo với phương nằm ngang một góc \[30^\circ \], phương nhìn \[BC\] tạo với phương nằm ngang một góc \[15^\circ 30'\]. Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất (làm tròn đến hàng phần trăm)?
134,7(m).
126,21(m).
77,77(m).
143,7(m).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một công ty may mặc có hai loại máy là máy cắt vải CNC và máy may công nghiệp để sản xuất hai loại sản phẩm áo sơ mi nam và quần tây nữ. Để sản xuất 1 cái áo sơ mi nam cần dùng máy cắt vải CNC trong 2 giờ và dùng máy may công nghiệp trong 1 giờ. Để sản xuất 1 cái quần tây nữ cần dùng máy cắt vải CNC trong 1 giờ và dùng máy may công nghiệp trong 3 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy cắt vải CNC làm việc không quá 8 giờ một ngày, máy may công nghiệp làm việc không quá 9 giờ một ngày. Một cái áo sơ mi nam lãi 83 ngàn đồng và một cái quần tây nữ lãi 87 ngàn đồng. Gọi \(x\), \(y\) lần lượt là số cái áo sơ mi nam và quần tây nữ cần sản xuất. Xét tính đúng-sai của các khẳng định sau:
a) \(2x + y - 8 \ge 0\).
b) Với \(x = 4,y = 4\) thì lợi nhuận thu được là lớn nhất.
c) Lợi nhuận lớn nhất đạt được là 428 ngàn đồng.
d) \(x + 3y - 9 \le 0\).
Cho các tập hợp \(C = \left\{ {1;2;3} \right\},D = \left\{ {\left. {x \in {\mathbb{N}^*}} \right|x \le 2} \right\},E = \{ \left. {x = 3n} \right|n \in \mathbb{N},n < 4\} \). Xét tính đúng sai của các khẳng định sau:
a) Tập hợp \(D\) là tập con của tập hợp \(C\).
b) Tập hợp \(D\) có 2 phần tử
c) Tập hợp \(E\) có 3 phần tử
d) Tập hợp \(E\) là tập con của tập hợp \(C\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
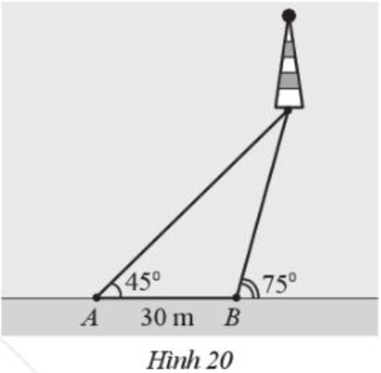
Một người đi dọc bờ biển từ vị trí \(A\) đến vị trí \(B\) và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí \(A\), \(B\) tới ngọn hải đăng với đường đi của người qunn sát lần lượt là \(45^\circ \) và \(75^\circ \). Biết khoảng cách giữa hai vi trí \(A\), \(B\) là 30m (Hình 20). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Cho hai tập hợp \(A = ( - \infty ;m),\,\,B = \left( {\frac{4}{m}; + \infty } \right)\). Có bao nhiêu giá trị nguyên của \(m\) trong khoảng \(\left( {0;10} \right)\) để \(A \cap B \ne \emptyset \).
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki-lô-gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi ki-lô-gam thịt lợn (heo) chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là \(1,6\;kg\) thịt bò và \(1,1\;kg\) thịt lợn; giá \(1\;kg\) thịt bò là 200000 đồng, \(1\;kg\) thịt lợn là 160000 đồng. Hỏi gia đình đó cần mua bao nhiêu ki-lô-gam thịt bò để đảm bảo cung cấp đủ lượng protein, lipit cho gia đình và có chi phí là ít nhất?
Bạn An thống kê số ngày có mưa và có nắng tại sân nhà của mình vào khung giờ từ 12 giờ đến 13 giờ trong tháng 8 năm 2024 và được kết quả như sau: 12 ngày có mưa, 24 ngày có nắng, trong đó có 10 ngày vừa có cả mưa và có cả nắng. Trong khoảng thời gian bạn An thống kê, số ngày không có mưa và cũng không có nắng là?
Cho \(\tan \alpha = - 2\)với \(\alpha \left( {{0^ \circ } \le \alpha \le {{180}^0}} \right)\). Tính \(\cos \alpha \) và \(\sin \alpha \).
Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên, người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang \(35^\circ \)và lần thứ hai, người này quan sát tại sân thượng của cùng tòa nhà đó, với phương nhìn tạo với phương nằm ngang \(15^\circ \). Tính chiều cao ngọn núi, biết rằng tòa nhà cao \(60m\).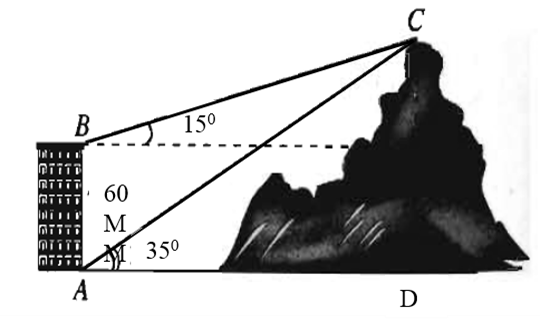
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa \(15\) gam hương liệu hòa tan, \(10\) lít nước và \(450\) gam đường để pha chế hai loại nước A và B; Để pha chế \(1\) lít nước cần \(50\) gam đường, \(1\) lít nước và \(0,6\) gam hương liệu. Để pha chế \(1\) lít nước cần \(20\) gam đường, \(1\) lít nước và \(1,5\) gam hương liệu. Mỗi lít nước nhận được \(70\) điểm thưởng, mỗi lít nước nhận được \(90\) điểm thưởng. Để đội chơi được số điểm thưởng là lớn nhất thì cần pha chế \(a\) lít nước và \(b\) lít nước. Tính tổng \(a + b\).








