Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 02
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y - 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
\(Q( - 1;0)\)
\(P(1;3)\)
\(N( - 1;1)\)
\(M(0;1)\)
Hãy liệt kê các phần tử của tập hợp \[X = \left\{ {x \in \mathbb{R}|2{x^2} - 5x + 3 = 0} \right\}\].
\(X = \left\{ 0 \right\}\).
\(X = \left\{ {\frac{3}{2}} \right\}\).
\(X = \left\{ {1;\frac{3}{2}} \right\}\).
\(X = \left\{ 1 \right\}\).
Tìm số các mệnh đề đúng trong các mệnh đề dưới đây.
i) \(\forall x \in \mathbb{R},\,2x + 1 > 0\).
iii) \(\exists x \in \mathbb{Q},\,{x^2} = 5\).
ii) \(\forall x \in \mathbb{R},\,{x^2} + 1 > 0\).
iv) \(\exists x \in \mathbb{R},\,{(x - 3)^2} \le 0\).
\(3\).
\(2\).
\(1\).
\(4\).
Hỏi cặp số \[\left( {1\,;\, - 1} \right)\]là nghiệm của bất phương trình nào sau đây?
\[ - x - y < 0\].
\[x + y - 3 > 0\].
\[ - x - 3y - 1 < 0\].
\[x + 3y + 1 < 0\].
Cho tập hợp \(A = \left\{ {x \in N\left| {x \le 5} \right.} \right\}\). Tập \(A\) được viết dưới dạng liệt kê các phần tử là.
\(A = \left\{ {0;1;2;3;4;5} \right\}\).
\(A = \left\{ {1;2;3;4;5} \right\}\).
\(A = \left\{ {0;1;2;3;4} \right\}\).
\(A = \left\{ {1;2;3;4} \right\}\).
Giá trị lớn nhất của biểu thức\[F\left( {x;y} \right) = x + 2y\], với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\) là
\(6\).
\[8\].
\[12\].
\[10\].
Cho tập hợp \(A = \left\{ {a = 3n|n \in {\mathbb{N}^*}} \right\}\), \(B = \left\{ {b \in \mathbb{N}|0 < b \le 9} \right\}\). Khẳng định nào sau đây là không đúng?
\(18 \in {\rm{A}}{\rm{,9}} \in A,9 \in B\).
\(15 \in {\rm{A}},15 \notin B\).
\(B \subset A\).
\(A \cap B = \left\{ {3;6;9} \right\}\).
Đường thẳng \(d:2x - y - 2 = 0\) chia mặt phẳng tọa độ thành hai miền \(I\), \(II\) là hai nửa mặt phẳng có bờ là đường thẳng \(d\) (Hình vẽ bên).
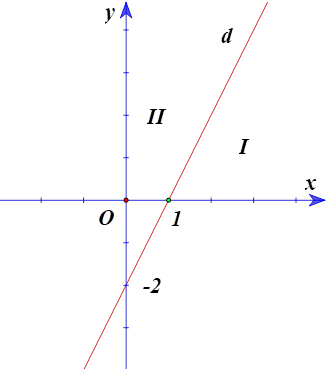
Xác định miền nghiệm của bất phương trình \(2x - y - 2 \ge 0\).
Nửa mặt phẳng \(I\) kể cả bờ \(d\).
Nửa mặt phẳng \(II\) kể cả bờ \(d\).\
Nửa mặt phẳng \(I\) bỏ đi đường thẳng \(d\).
Nửa mặt phẳng \(II\) bỏ đi đường thẳng \(d\).
Cho biết \(\sin \frac{\alpha }{3} = \frac{3}{5}\). Giá trị của \(P = 3{\sin ^2}\frac{\alpha }{3} + 5{\cos ^2}\frac{\alpha }{3}\) là
\(P = \frac{{111}}{{25}}\).
\(P = \frac{{107}}{{25}}\).
\(P = \frac{{105}}{{25}}\).
\(P = \frac{{109}}{{25}}\).
Cho \[0^\circ < \alpha < 90^\circ \]. Khẳng định nào sau đây đúng?
\[\cos \left( {90^\circ + \alpha } \right) = - \sin \alpha \].
\[\tan \left( {90^\circ + \alpha } \right) = \cot \alpha \].
\[\sin \left( {90^\circ + \alpha } \right) = - \cos \alpha \].
\[\cot \left( {90^\circ + \alpha } \right) = \tan \alpha \].
Tam giác \[ABC\] có \(\cos \left( {A + B} \right) = - \frac{1}{8}\), \[AC = 4\], \[BC = 5\]. Tính cạnh \[AB\]
\(\sqrt {46} \).
\(5\sqrt 2 \).
\[11\].
\[6\].
Hai chiếc tàu thủy cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \({60^0}\). Tàu thứ nhất chạy với tốc độ \(20\,km/h\), tàu thứ hai chạy với tốc độ \(30\,km/h\). Hỏi sau \(3\)giờ hai tàu cách nhau bao nhiêu \(km\).
\(30\sqrt 7 \).
\(20\sqrt 7 \).
\(35\sqrt 7 \).
\(10\sqrt 7 \).
PHẦN II. Câu trắc nghiệm đúng sai.Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tập hợp \(A = \{ n \in {\mathbb{N}^*}\mid \left( {n - 2} \right)\left( {n - 1} \right)\left( {n + 3} \right) = 0\} \) và \(B = \{ x \in \mathbb{R}\mid {x^2} + 6x = 0\} \). Hãy xét tính đúng sai các khẳng định sau:
a) Số tập con của tập hợp \(B\) bằng \(3\).
b) Số phần tử của tập hợp \(A\) là \(2\).
c) \(A \cap B = \emptyset \).
d) \(A \cup B = \{ - 6,0,1,2\} \).
Cho hai bất phương trình \(2x - 3y \le 2\) và \(5x + y \ge - 6\) và \(5x + y \ge - 6\)
a) Gốc tọa độ nằm trong miền nghiệm của bất phương trình \(2x - 3y \le 2\).
b) Tồn tại duy nhất \(1\) cặp số \((x;y)\) sao cho \(x,y\) không là số nguyên dương thuộc bất phương trình \(5x + y \ge - 6\).\(O(0;0)\)
c) Giá trị nhỏ nhất của biểu thức với \(x,y\) thõa mãn hệ bất \(O(0;0)\)trình \((*)\) là \(P = - \frac{6}{5}\).
d) Miền nghiệm biểu diễn của hệ bất phương trình \((*)\) là một tứ giác nội tiếp đường tròn khi biểu diễn lên hệ trục tọa độ \(Oxy\). Hệ bất phương trình \((*)\) \(\left\{ {\begin{array}{*{20}{l}}{2x - 3y \le 2}\\{5x + y \ge - 6}\\{y \le 0}\\{x \le 0}\end{array}} \right.\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời từ câu 1 đến câu 4.
Cho hai tập hợp \(A = (2m - 7;m - 5],B = [ - 3;1)\). Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\)?
Có ba nhóm máy \(X,Y,Z\) dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho trong bảng sau:
Một đơn vị sản phẩm loại I lãi 3 nghìn đồng, một đơn vị sản phẩm loại II lãi 5 nghìn đồng. Công ty cần sản suất tổng số bao nhiêu sản phẩm loại 1 và sản phẩm loại 2 đề cho tổng số tiền lãi thu được là cao nhất?
Khối 10 của một trường THPT có 440 em học sinh, trong đó có 250 em thích môn Văn, 210 em thích môn Toán, 240 em thích môn Anh, 65 em không thích môn nào, 75 em thích cả ba môn. Hỏi số em chỉ thích một trong ba môn trên là bao nhiêu?
Hai bạn An và Bình cùng xuất phát từ điểm , đi theo hai hướng khác nhau và tạo với nhau một góc \(40^\circ \) để đến đích là điểm \[D\], góc \[PAD\] bằng \(100^\circ \). Biết rằng họ dừng lại để ăn trưa lần lượt tại \[A\] và \[B\] (như hình vẽ minh hoạ).
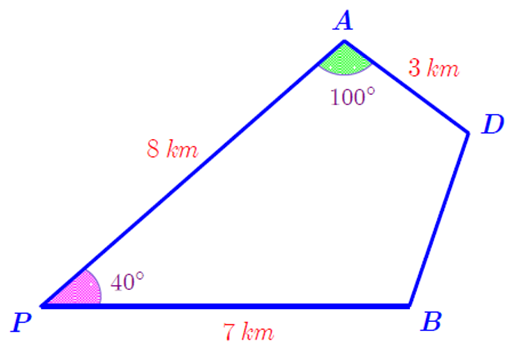Hỏi bạn Bình phải đi bao xa nữa để đến được đích (làm tròn đến 1 chữ số sau dấu thập phân)?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho \(\tan \alpha = 3\), giá trị của biểu thức \(A = \frac{{ - \sin \alpha + 3\cos \alpha }}{{\sin \alpha - \cos \alpha }}\).
Bạn Linh đự định làm tối đa \(9\) sản phẩm trang trí để bày bán tại gian hàng hội chợ của trường. Nếu làm một sản phẩm loại \(A\) thì cần \(40\) phút và thu được \(15\) nghìn đồng. Nếu làm một sản phẩm loại \(B\) thì cần \(60\) phút và thu được \(20\) nghìn đồng. Hãy tính số tiền nhiều nhất mà Linh có thế thu được (đơn vị nghìn đồng)? Biết bạn Linh chỉ có tối đa \(8\) giờ cho việc làm các sản phẩm trang trí.
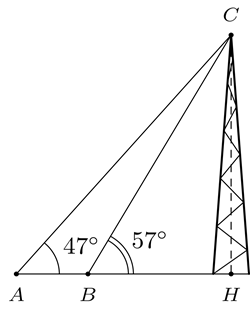
Để đo chiều cao \(CH\) của một tháp truyền hình, người ta chọn hai điểm quan sát \(A\), \(B\) trên mặt đất (hình vẽ). Biết , và \(AB = 63m\), tính chiều cao của tháp. 
