Bộ 10 đề thi giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 01
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tập hợp \(A = \left[ { - 3;5} \right]\). Viết lại tập hợp \(A\) bằng cách chỉ ra tính chất đặc trưng.
\(A = \left\{ {\left. {x \in \mathbb{N}} \right| - 3 \le x \le 5} \right\}\).
\(A = \left\{ {\left. {x \in \mathbb{R}} \right| - 3 < x < 5} \right\}\).
\(A = \left\{ {\left. {x \in \mathbb{R}} \right| - 3 \le x \le 5} \right\}\).
\(A = \left\{ {\left. {x \in \mathbb{Z}} \right| - 3 \le x \le 5} \right\}\).
Trong các câu sau, cầu nào là mệnh đề đúng?
Nếu \(a \ge b\) thì \({a^2} \ge {b^2}\).
Nếu một tam giác có một góc bằng \(60^\circ \)thì tam giác đó đều.
Nếu bạn tự tin thì bạn thành công.
Nếu \(a\) chia hết cho \(9\) thì \(a\) chia hết cho \(3\).
Tìm cặp số là nghiệm của bất phương trình \[ - x + 3y - 2 > 0\]
\(\left( {0;0} \right)\).
\(\left( { - 1;2} \right)\).
\(\left( {3;1} \right)\).
\(\left( {1;1} \right)\)
Cặp số nào sau đây là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y \le 8\\3x - y > 3\end{array} \right.\) ?
\(\left( {2;3} \right)\).
\(\left( {4;1} \right)\).
\(\left( {1; - 1} \right)\).
\(\left( {0;4} \right)\).
Hãy viết lại tập hợp \[X = \left\{ {x \in \mathbb{R}|2{x^2} - 5x + 3 = 0} \right\}\] dưới dạng liệt kê.
\[X = \left\{ 1 \right\}\].
\[X = \emptyset \].
\[X = \left\{ {\frac{3}{2}} \right\}\].
\[X = \left\{ {1;\frac{3}{2}} \right\}\].
Tam giác \[ABC\] có \(BC = \sqrt 5 \), \[AC = 3\] và \(\cot C = 2\). Tính cạnh \[AB\]
\[6\].
\(2\sqrt {10} \).
\(\sqrt 2 \).
\(\frac{9}{5}\).
Tam giác \[ABC\] vuông ở \[A\] và có \(BC = 2AC\). Tính \(\cos (\overrightarrow {AC} ,\overrightarrow {CB} ).\)
\(\cos (\overrightarrow {AC} ,\overrightarrow {CB} ) = \frac{1}{2}\).
\(\cos (\overrightarrow {AC} ,\overrightarrow {CB} ) = - \frac{1}{2}\).
\(\cos (\overrightarrow {AC} ,\overrightarrow {CB} ) = \frac{{\sqrt 3 }}{2}\).
\(\cos (\overrightarrow {AC} ,\overrightarrow {CB} ) = - \frac{{\sqrt 3 }}{2}\).
Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình \(2x - 3y - 6 \le 0\) (miền không tô đậm kể cả bờ)?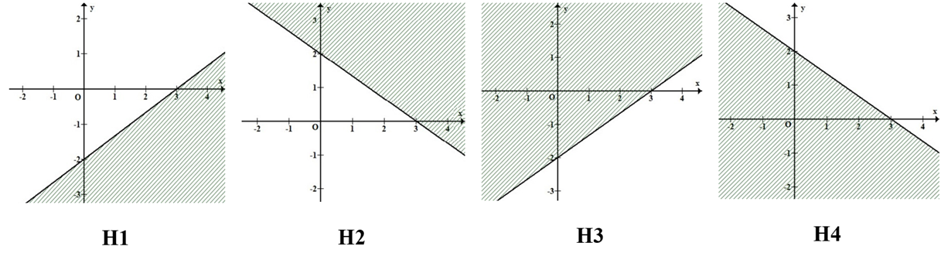
H2
H4
H3
H1
Cho \[{\rm{cos}}\alpha \;{\rm{ = }}\;\frac{{ - 2}}{5}\left( {90^\circ < \alpha < 180^\circ } \right)\]. Khi đó \[\tan \alpha \] bằng
\(\frac{{\sqrt {21} }}{5}\).
\( - \frac{{\sqrt {21} }}{5}\).
\( - \frac{{\sqrt {21} }}{2}\).
\(\frac{{\sqrt {21} }}{3}\).
Cho hai tập hợp \(X = \left\{ {1;\;3;\;5;\;7} \right\}\) và \(Y = \left\{ {5;\;6;\;7;\;8} \right\}\). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
\(\left\{ {5;\;7} \right\}\).
\(\left\{ {1;\;3;\;5;\;6;\;7;\;8} \right\}\).
\(\left\{ {1;\;3;\;7} \right\}\).
\(\left\{ {1;\;3;\;5;\;7} \right\}\).
Giá trị nhỏ nhất của biết thức trên \(F = y - x\) miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \le 2}\\{x - y \le 2}\\{5x + y \ge - 4}\end{array}} \right.\) là
\[\min F = 2\] khi \[x = - 1,{\rm{ }}y = 1\].
\[\min F = - 2\] khi \[x = 1,{\rm{ }}y = - 1\].
\[\min F = 2\] khi \[x = 0,{\rm{ }}y = 2\].
\[\min F = - 1\] khi \[x = 0,{\rm{ }}y = - 1\].
Từ vị trí \[A\] người ta quan sát một cây cao.
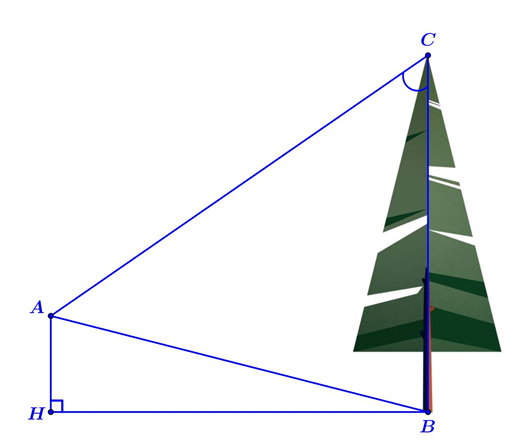Biết \[AH = 4{\rm{m}}\], \[HB = 20{\rm{m}}\], \[\widehat {BAC} = {45^^\circ }\]. Khi đó chiều cao của cây (làm tròn đến hàng phần mười) bằng
\[17,3{\rm{m}}\].
\[17,2{\rm{m}}\].
\[17,4{\rm{m}}\].
\[17,6{\rm{m}}\].
PHẦN II. Câu trắc nghiệm đúng sai.Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích \(8\) hecta. Nếu trồng \(1\) hecta khoai lang thì cần \(10\) ngày công và thu được \(20\) triệu đồng. Nếu trồng \(1\) hecta khoai mì thì cần \(15\) ngày công và thu được \(25\) triệu đồng. Biết rằng, bác Năm chỉ có thể sử dụng được không quá \(90\) ngày công cho việc trồng khoai lang và khoai mì. Gọi \(x\), \(y\) lần lượt là số hecta trồng khoai lang và khoai mì \((x\), \(y \ge 0)\).
a) Số tiền bác Năm thu được \(F = 20x + 25y\) (triệu đồng).
b) Để thu nhiều tiền nhất bác Năm cần trồng \(6\) hecta khoai lang và \(2\) hecta khoai mì.
c) Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ \(Oxy\) ta được miền đa giác \(OABC\) với \(O(0;0)\), \(A(2;6)\), \(B(6;0)\), \(C(8;0)\) kể cả cạnh của tứ giác.
d) Hệ bất phương trình mô tả các điều kiện ràng buộc của bài toán là \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{y \ge 0}\\{x + y \le 8}\\{10x + 15y \le 90.}\end{array}} \right.\).
Cho tập hợp \(X = \left\{ { - 3; - 1;0;1;3} \right\}\). Xét tính đúng sai của các khẳng định sau:
a) \( - 1\)là một phần tử của tập hợp \(X\).
b) Số tập con của tập hợp \(X\)là \(32\) tập hợp.
c) Số tập hợp con của \(X\) có \(2\) phần tử là \(10\).
d) Tính chất đặc trưng của tập hợp \(X\) là \(X = \left\{ {x \in N:2x + 1 \le 5} \right\}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Bạn \(A\) Súa thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: 14 ngày có mưa, 15 ngày có sương mù, trong đó 10 ngày có cả mưa và sương mù. Hỏi trong tháng 3 đó có bao nhiêu ngày không có mưa và không có sương mù?
Một cây cao bị nghiêng so với mặt đất góc \({78^^\circ }\). Từ vị trí \(C\) cách gốc cây \(20\;m\), người ta tiến hành đo đạc và thu được kết quả: \(\widehat {ACB} = {50^^\circ }\) với \(B\) là vị trí ngọn cây.
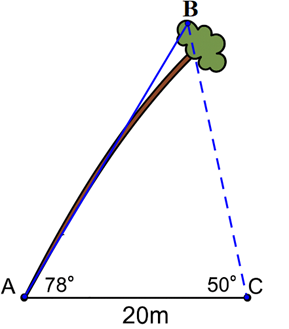
Tính khoảng cách từ gốc cây (điểm \(A\)) đến ngọn cây (điểm \(B\)) (làm tròn kêt quả đến hàng phần mười theo đơn vị mét).
Một công ty \(X\) có 2 phân xưởng \(A,B\) cùng sản xuất 2 loại sản phẩm \(M,N\). Số đơn vị sản phẩm các loại được sản xuất ra và chi phí mỗi giờ hoạt động của \(A,B\) như sau:
Công ty nhận được yêu cầu đặt hàng là 5000 đơn vị sản phẩm \(M\) và 3000 đơn vị sản phẩm \(N\).
Công ty đã tìm được cách phân phối thời gian cho mỗi phân xưởng hoạt động thỏa mãn yêu cầu đơn đặt hàng và chi phí thấp nhất. Hỏi chi phí thấp nhất bằng bao nhiêu triệu đồng?
Cho hai tập hợp: \(A = [m - 3;m + 2],\,\,B = ( - 3;5)\) với \(m \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\)?
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất \(45\) radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất \(80\) radio/ngày. Để sản xuất một chiếc radio kiểu một cần \(12\) linh kiện, để sản xuất một chiếc radio kiểu hai cần \(9\) linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là \(250000\) đồng, lãi thu được khi bán một chiếc radio kiểu hai là \(180000\) đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là \(900\). Gọi \({x_0}\), \({y_0}\) lần lượt là số radio kiểu một và radio kiểu hai sản suất được trong một ngày để tiền lãi thu được là nhiều nhất. Tính tổng \(T = {x_0} + 2{y_0}\).
Các góc nhìn đến đỉnh núi so với mực nước biển được đo từ hai đèn tín hiệu A và B trên biển được thể hiện trên hình vẽ. Nếu các đèn tín hiệu cách nhau 1536 m thì ngọn núi cao bao nhiêu (tính gần đúng sau dấu phẩy hai chữ số)?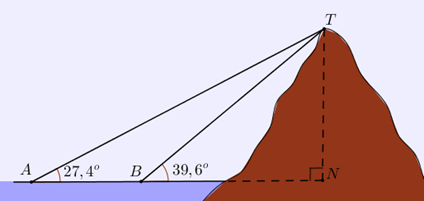
Cho góc \(a\) thỏa mãn \(\cot a = \frac{5}{2}\). Tính giá trị biểu thức \(P = \frac{{ - 2\cos a + 4\sin a}}{{ - 4\cos a - \sin a}}\).
