Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 9
48 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Góc lượng giác nào sau đây có cùng điểm cuối với góc \(\frac{{7\pi }}{4}?\)
\[ - \frac{\pi }{4}.\]
\[\frac{\pi }{4}.\]
\[\frac{{3\pi }}{4}.\]
\[ - \frac{{3\pi }}{4}.\]
Cho hai góc lượng giác có và Khẳng định nào sau đây đúng?
\(Ou\) và \(Ov\) vuông góc.
\(Ou\) và \(Ov\) đối nhau.
\(Ou\) và \(Ov\) trùng nhau.
Tạo với nhau một góc \(\frac{\pi }{4}\).
Điểm cuối của góc lượng giác \(\alpha \) ở góc phần tư thứ mấy nếu \(\sin \alpha ,\,\,\tan \alpha \) trái dấu?
Thứ I.
Thứ II hoặc IV.
Thứ I hoặc IV.
Thứ II hoặc III.
Cho \(\cos \alpha = \frac{1}{3}\) và \(\frac{{7\pi }}{2} < \alpha < 4\pi .\) Khẳng định nào sau đây là đúng?
\[\sin \alpha = - \frac{{2\sqrt 2 }}{3}.\]
\[\sin \alpha = \frac{{2\sqrt 2 }}{3}.\]
\[\sin \alpha = \frac{2}{3}.\]
\[\sin \alpha = - \frac{2}{3}.\]
Biểu thức \(\frac{{\sin \left( {a + b} \right)}}{{\sin \left( {a - b} \right)}}\) bằng biểu thức nào sau đây?
\(\frac{{\sin \left( {a + b} \right)}}{{\sin \left( {a - b} \right)}} = \frac{{\sin a + \sin b}}{{\sin a - \sin b}}\).
\(\frac{{\sin \left( {a + b} \right)}}{{\sin \left( {a - b} \right)}} = \frac{{\sin a - \sin b}}{{\sin a + \sin b}}\).
\(\frac{{\sin \left( {a + b} \right)}}{{\sin \left( {a - b} \right)}} = \frac{{\tan a + \tan b}}{{\tan a - \tan b}}\).
\(\frac{{\sin \left( {a + b} \right)}}{{\sin \left( {a - b} \right)}} = \frac{{\cot a + \cot b}}{{\cot a - \cot b}}\).
Rút gọn biểu thức \(A = \frac{{2{{\cos }^2}x - 1}}{{\sin x + \cos x}},\) ta được kết quả
\(A = \sin x + \cos x.\)
\(A = \cos x - \sin x.\)
\(A = \cos 2x - \sin 2x.\)
\(A = \cos 2x + \sin 2x.\)
Trong các khẳng định sau đây, khẳng định nào đúng?
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \(y = \cos x\) là hàm số lẻ.
Hàm số \(y = \tan x\) là hàm số lẻ.
Hàm số \(y = \cot x\) là hàm số chẵn.
Tìm tập giá trị \(T\) của hàm số \(y = 3\cos 2x + 5.\)
\(T = \left[ { - 1\,;\,\,1} \right].\)
\(T = \left[ { - 1\,;\,\,11} \right].\)
\(T = \left[ {2\,;\,\,8} \right].\)
\(T = \left[ {5\,;\,\,8} \right].\)
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(\sin x = m + 1\) có nghiệm?
\(m \ge 1.\)
\(0 \le m \le 1.\)
\(m \le 0.\)
\( - 2 \le m \le 0.\)
Nghiệm nào của phương trình \(\tan x = \frac{{ - \sqrt 3 }}{3}\) được biểu diễn trên đường tròn lượng giác trong hình bên dưới là những điểm nào?
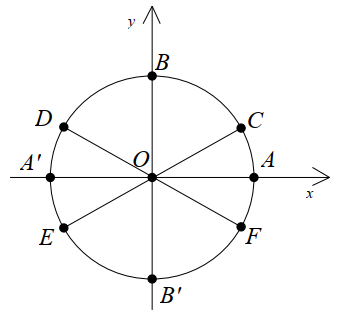
Điểm \(F,\) điểm \(D.\)
Điểm \(C,\) điểm \(F.\)
Điểm \(C,\) điểm \(D,\) điểm \(E,\) điểm \(F.\)
Điểm \(E,\) điểm \(F.\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 1 + {2^n}.\) Khi đó số hạng \({u_{2018}}\) bằng
\({2^{2018}}.\)
\(2017 + {2^{2017}}.\)
\(1 + {2^{2018}}.\)
\(2018 + {2^{2018}}.\)
Tìm \(x\) biết: \(\left( {x + 3} \right) + \left( {x + 7} \right) + \left( {x + 11} \right) + \cdots + \left( {x + 79} \right) = 860.\)
\(x = 1.\)
\(x = 2.\)
\(x = 3.\)
\(x = 4.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 9\) và công sai \(d = 2.\) Giá trị của \({u_2}\) bằng
11.
\(\frac{9}{2}.\)
18.
7.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 1\) và công sai \(d = 2.\) Tổng \({S_{10}} = {u_1} + {u_2} + {u_3} + \cdots + {u_{10}}\) bằng
\({S_{10}} = 110.\)
\({S_{10}} = 100.\)
\({S_{10}} = 21.\)
\({S_{10}} = 19.\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = - 2\) và công bội \(q = 3.\) Số hạng \({u_2}\) là
\({u_2} = - 6.\)
\({u_2} = 6.\)
\({u_2} = 1.\)
\({u_2} = - 18.\)
Cho cấp số nhân có \({u_1} = - 3;\,\,q = \frac{2}{3}.\) Số \(\frac{{ - 96}}{{243}}\) là số hạng thứ mấy của cấp số này?
Thứ 5.
Thứ 6.
Thứ 7.
Không phải là số hạng của cấp số.
Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt phẳng phân biệt từ các điểm đó?
3.
4.
2.
6.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với đáy lớn \(AD,\,\,AD = 2BC.\) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) là
\(SA\).
\(AC\).
\(SD\).
\(SO\).
Chọn mệnh đề sai trong các mệnh đề sau.
Hai đường thẳng phân biệt có không quá một điểm chung.
Hai đường thẳng cắt nhau thì không song song với nhau.
Hai đường thẳng không có điểm chung thì song song với nhau.
Hai đường thẳng chéo nhau thì không có điểm chung.
Cho tứ diện \(ABCD.\) Trên các cạnh \(AB,\,\,AD\) lần lượt lấy các điểm \(M,\,\,N\) sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}.\) Gọi \(P,\,\,Q\) lần lượt là trung điểm các cạnh \(CD,\,\,CB.\) Mệnh đề nào sau đây đúng?
Tứ giác \(MNPQ\) không có các cặp cạnh đối song song.
Tứ giác \(MNPQ\) là hình bình hành.
Bốn điểm \(M,\,\,N,\,\,P,\,\,Q\) không đồng phẳng.
Tứ giác \(MNPQ\) là hình thang.
II. Tự luận (4,0 điểm)
(1,0 điểm)Giải phương trình:
a) \(\sqrt 3 \tan x + 3 = 0\); b) \(\cos \left( {2x + \frac{\pi }{3}} \right) - \sin 5x = 0\).
(0,5 điểm) Tính tổng: \(S = \left( {1 - \frac{1}{2}} \right) + \left( {1 - \frac{1}{4}} \right) + \left( {1 - \frac{1}{8}} \right) + \cdots + \left( {1 - \frac{1}{{{2^n}}}} \right).\) Tính \({S_{10}}.\)
(1,5 điểm)Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang \[(AD\] là đáy lớn, \[BC\] là đáy nhỏ). Gọi \[E,{\rm{ }}F\] lần lượt là trung điểm của \[SA\] và \[SD.{\rm{ }}K\] là giao điểm của các đường thẳng \[AB\] và \[CD.\]
a) Tìm giao điểm \[M\] của đường thẳng \[SB\] và mặt phẳng \(\left( {CDE} \right)\).
b) Đường thẳng \[SC\] cắt mặt phẳng \(\left( {EFM} \right)\) tại \[N.\] Tứ giác \[EFNM\] là hình gì?
c) Chứng minh các đường thẳng \[AM,{\rm{ }}DN,{\rm{ }}SK\] đồng quy.
(1,0 điểm)Sinh nhật bạn của An vào ngày 01 tháng năm. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo 100 đồng vào n gày 01 tháng 01 năm 2016, sau đó cứ liên tục ngày sau hơn ngày trước 100 đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền?
I. Trắc nghiệm (6 điểm)
Mệnh đề phủ định của mệnh đề “Nghiệm của phương trình \(3{x^2} + 10 = 0\) là số hữu tỉ” là
“Nghiệm của phương trình \(3{x^2} + 10 = 0\) không là số hữu tỉ”;
“Nghiệm của phương trình \(3{x^2} + 10 = 0\) không là vô tỉ”;
“Phương trình \(3{x^2} + 10 = 0\) vô nghiệm”;
“Nghiệm của phương trình \(3{x^2} + 10 = 0\) không là số nguyên”.
Mệnh đề “Nếu tam giác đều thì tam giác đó có ba cạnh bằng nhau” có mệnh đề đảo là
“Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều”;
“Nếu tam giác không đều thì tam giác đó không có ba cạnh bằng nhau”;
“Nếu tam giác đều thì tam giác đó không có ba cạnh bằng nhau”;
“Nếu tam giác có ba cạnh bằng nhau thì tam giác đó không phải là tam giác đều”;
Khẳng định đúng là
\(3 \notin \left[ {3;9} \right]\);
\(3 \in \left( { - \infty ;2} \right)\);
\(3 \in \left( { - 4;3} \right]\);
\(3 \notin \left( { - 5; + \infty } \right)\).
Cho tập hợp \(A = \left\{ {4;\frac{1}{2};\sqrt 5 ;0,3} \right\}\) và \(B = \left\{ {x \in A|x \in \mathbb{Q}} \right\}\). Viết tập hợp \(B\) dưới dạng liệt kê các phần tử của tập hợp ta được
\(B = \left\{ {4;\frac{1}{2};0,3} \right\}\);
\(B = \left\{ 4 \right\}\);
\(B = \left\{ {\frac{1}{2};0,3} \right\}\);
\(B = \left\{ {4;\frac{1}{2}} \right\}\).
Cho số thực \(x\), khi \(x < 4\) thì \(x\) thuộc tập hợp nào sau đây?
\(\left( { - \infty ;3} \right)\);
\(\left( {4;10} \right]\);
\(\left( { - \infty ;4} \right)\);
\(\left( { - \infty ;4} \right]\).
Cặp số nào sau đây là một nghiệm của bất phương trình bậc nhất hai ẩn \(x - y + 4 < 0\) ?
\(\left( {1;6} \right)\);
\(\left( {2;3} \right)\);
\(\left( {0; - 3} \right)\);
\(\left( {1;5} \right)\).
Nửa mặt phẳng (không kể bờ) có bờ là đường thẳng \(2x - y = 5\) và không chứa điểm \(O\left( {0;0} \right)\) là miền nghiệm của bất phương trình bậc nhất hai ẩn nào dưới đây?
\(2x - y < 5\);
\(2x - y > 5\);
\(2x - y \le 5\);
\(2x - y \ge 5\).
Điểm \(A\left( {2;5} \right)\) thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?
\(\left\{ \begin{array}{l}2x + 6y < 4\\x - 4y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}2x + 3y < 100\\x - y \le 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y < 10\\5x - y < 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 3y > 2\\x - y < - 6\end{array} \right.\).
Trong các hệ bất phương trình sau, hệ nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x - {y^2} \ge 2\\x - 4y < 2\end{array} \right.\);
\(\left\{ \begin{array}{l}2{x^2} - {y^2} \ge 0\\x - 4y < 4\end{array} \right.\);
\(\left\{ \begin{array}{l}4x - 9y > - 3\\xy > 7\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y < 1\\2x - y - 7 > 0\end{array} \right.\).
Cho góc \(\beta \) biết \(0^\circ \le \beta \le 180^\circ \), khẳng định nào sau đây là sai ?
\(\tan \beta = - \tan \left( { - \beta } \right)\);
\[\cos \left( { - \beta } \right) = \cos \beta \];
\(\sin \left( {180^\circ - \beta } \right) = \sin \beta \);
\(\cot \beta = \cot \left( { - \beta } \right)\).
Cho tam giác có độ dài ba cạnh lần lượt là \(a\), \(b\), \(c\), các góc đối diện các cạnh đó lần lượt là \(\alpha \), \(\beta \), \(\varphi \). Áp dụng định lí sin cho tam giác này ta có:
\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \varphi }}\);
\(\frac{a}{{\sin \varphi }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \alpha }}\);
\({a^2} = {b^2} + {c^2} - 2bc\sin \alpha \);
\({a^2} = {b^2} + {c^2} - 2bc\sin \alpha \).
Cho tam giác \(ABC\) có \(AB = 4\,\,{\rm{cm}}\), \(AC = 6\,\,{\rm{cm}}\), \(BC = 7\,{\rm{cm}}\). Diện tích (làm tròn đến hàng phần trăm) của tam giác \(ABC\) là
\(11,96\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\);
\(11,97\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\);
\(11,98\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\);
\(11,99\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho hình ảnh dưới, khẳng định nào sau đây là đúng ?

\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) có cùng điểm cuối;
\[\overrightarrow {EF} = \overrightarrow {EG} \];
Đường thẳng \(AE\) là giá của vectơ \(\overrightarrow {EG} \);
\[\overrightarrow {EF} \] và \[\overrightarrow {EG} \] là hai vectơ đối nhau.
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\). Cặp vectơ nào sau đây là cặp vectơ ngược hướng ?
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \);
\(\overrightarrow {AM} \) và \(\overrightarrow {BC} \);
\(\overrightarrow {BM} \) và \(\overrightarrow {MC} \);
\(\overrightarrow {BM} \) và \(\overrightarrow {CM} \).
Cho hình bình hành \(ABCD\), khẳng định nào sau đây thể hiện quy tắc ba điểm?
\[\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \];
\[\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \];
\[\overrightarrow {AB} = - \overrightarrow {CD} \];
\[\overrightarrow {AD} = \overrightarrow {BC} \].
Cho hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) như hình vẽ.
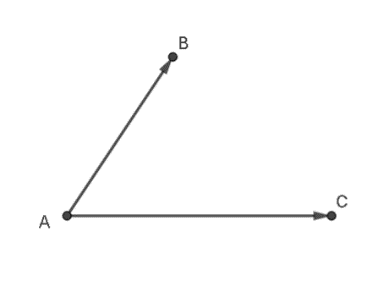
Hình vẽ biểu diễn vectơ hiệu \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AC} \) là
A. 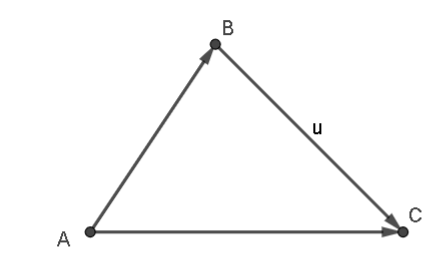 ;
;
B. 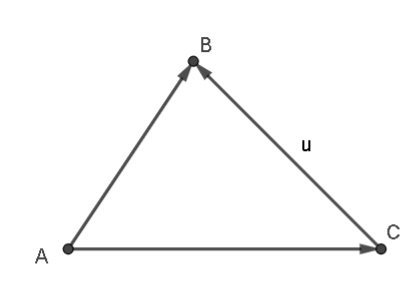 ;
;
C. 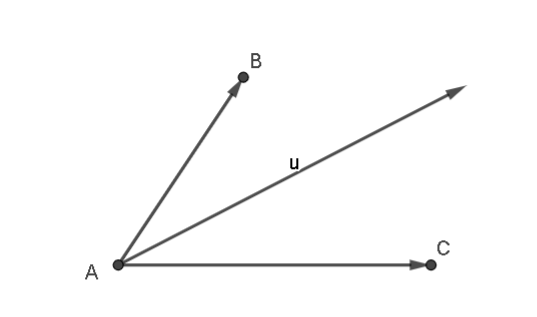 ;
;
D. 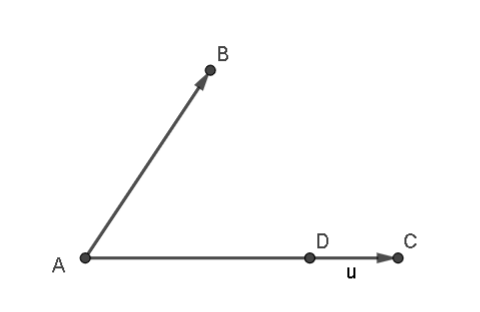 .
.
Biểu thức nào dưới đây là tích của một số với một vectơ ?
\(3\overrightarrow {AB} \);
\(\overrightarrow {AB} \cdot \overrightarrow {CD} \);
\(\overrightarrow {AB} + \overrightarrow {CD} \);
\(\overrightarrow 0 \cdot \overrightarrow {MN} \).
Cho tam giác \(ABC\) có \(D\), \(H\) lần lượt là trung điểm của \(AB\) và \(AC\) như hình vẽ.
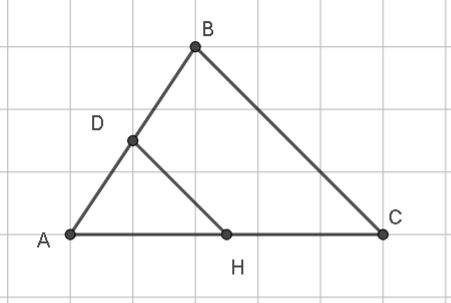
Khi đó ta có \(\overrightarrow {DH} = ...\overrightarrow {BC} \). Số thích hợp để điền vào chỗ chấm là
\(\frac{1}{2}\);
\(\frac{1}{3}\);
\(\frac{2}{3}\);
1.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ – không. Biết \(\overrightarrow a \cdot \overrightarrow b = - 1\) và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\). Khi đó: \(\left( {\overrightarrow a ,\overrightarrow b } \right) = ?\)
\(0^\circ \);
\(1^\circ \);
\(180^\circ \);
\(90^\circ \).
Cho tam giác \(ABC\) đều có \(AC = 11\,\,\,{\rm{cm}}\). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AC} = ?\)
121,5;
121;
60;
60,5.
II. Tự luận (4 điểm)
(1 điểm) Cho hai tập hợp \(A = \left( { - \infty ;2m} \right]\) và \(B = {\rm{[8}}; + \infty )\). Tìm \(m\) để \(A \cap B \ne \emptyset \).
(1 điểm) Một xưởng cơ khí có hai máy sản xuất là máy \(A\) và máy \(B\). Xưởng sản xuất hai loại sản phẩm là sản phẩm \(C\) và \(D\). Mỗi sản phẩm \(C\) lãi 60 000 đồng, mỗi sản phẩm loại \(D\) lãi 40 000 đồng. Để sản xuất được một sản phẩm \(C\) thì máy \(A\) phải hoạt động trong 3 giờ, máy \(B\) phải hoạt động trong 1 giờ. Để sản xuất được một sản phẩm \(D\) thì máy \(A\) phải hoạt động trong 2 giờ, máy \(B\) phải hoạt động trong 6 giờ. Một máy không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng, máy \(A\) không thể hoạt động quá 180 giờ và máy \(B\) không thể hoạt động quá 220 giờ (vì lí do bảo trì). Tính số tiền lãi lớn nhất xưởng có thể đạt được trong một tháng.
(1 điểm) Cho tam giác nhọn \(MNP\), biết \(MN = 6\,\,{\rm{cm}}\), \(MP = 1,5MN\), chu vi của tam giác \(MNP\) là 23 cm. Giải tam giác \(MNP\).
(1 điểm) Cho tam giác \(ABC\) có điểm \(D\)nằm trên cạnh \(BC\) sao cho \(DC = \frac{1}{2}BD\), đoạn thẳng \(AD\) có trung điểm \(E\). Một đường thẳng bất kì đi qua \(E\) cắt các cạnh \(AB\), \(AC\) lần lượt tại \(M\) và \(N\). Tính tỉ số \(2\frac{{AC}}{{AN}} + \frac{{AB}}{{AM}}\).