Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 7
48 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
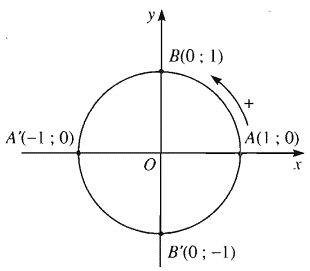
Trên đường tròn lượng giác ở hình vẽ bên, số đo của góc lượng giác \(\left( {OA,\,\,OB'} \right)\) là
\( - \frac{\pi }{4}.\)
\(\frac{\pi }{2}.\)
\( - \frac{\pi }{2}.\)
\(\frac{\pi }{4}.\)
Chọn khẳng định đúng. Trong hệ tọa độ \(Oxy,\) cho hai điểm \(M\) và \(N\) thuộc đường tròn lượng giác. Hai góc lượng giác \(\left( {Ox,\,\,OM} \right)\) và \(\left( {Ox,\,\,ON} \right)\) lệch nhau \(180^\circ .\)
\(M,\,\,N\)có tung độ và hoành độ đều bằng nhau.
\(M,\,\,N\)có tung độ và hoành độ đều đối nhau.
\(M,\,\,N\)có tung độ bằng nhau và hoành độ đối nhau.
\(M,\,\,N\)có hoành độ bằng nhau và tung độ đối nhau.
Cho hai góc nhọn \(\alpha \)và \(\beta \) phụ nhau. Hệ thức nào sau đây sai?
\(\sin \alpha = - \cos \beta \).
\(\cos \alpha = \sin \beta \).
\(\cos \beta = \sin \alpha \).
\(\cot \alpha = \tan \beta \).
Cho \(\frac{\pi }{2} < \alpha < \pi .\) Xác định dấu của biểu thức \(M = \cos \left( { - \frac{\pi }{2} + \alpha } \right) \cdot \tan \left( {\pi - \alpha } \right).\)
\(M \ge 0\).
\(M < 0.\)
\(M \le 0\).
\(M > 0.\)
Mệnh đề nào sau đây là đúng?
\(\tan \left( {x - y} \right) = \frac{{\tan x + \tan y}}{{\tan x\tan y}}\).
\(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 + \tan x\tan y}}\).
\(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 - \tan x\tan y}}\).
\(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{\tan x\tan y}}\).
Biểu thức rút gọn của \(A = \frac{{{{\tan }^2}a - {{\sin }^2}a}}{{{{\cot }^2}a - {{\cos }^2}a}}\) bằng
\({\tan ^6}a\).
\({\cos ^6}a\).
\({\tan ^4}a\).
\({\sin ^6}a.\)
Tập xác định của hàm số \(y = \tan x\) là
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
\(y = \sin \,x\cos 2x.\)
\(y = {\sin ^3}x.\cos \left( {x - \frac{\pi }{2}} \right).\)
\(y = \frac{{\tan \,x}}{{{{\tan }^2}x + 1}}.\)
\(y = \cos x{\sin ^3}x.\)
Nghiệm của phương trình \(\cot x = 3\) là
\(x \in \emptyset .\)
\(x = 3 + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = {\mathop{\rm arccot}\nolimits} 3 + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = {\mathop{\rm arccot}\nolimits} 3 + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Tất cả nghiệm của phương trình \(\tan \left( {3x + \frac{\pi }{4}} \right) = 0\) là
\(x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
\(x = k\frac{\pi }{3},k \in \mathbb{Z}\).
\(x = - \frac{\pi }{{12}} + k\frac{\pi }{3},k \in \mathbb{Z}\).
Cho dãy số có các số hạng đầu là: \[\frac{1}{3}\,;\,\,\frac{1}{{{3^2}}}\,;\,\,\frac{1}{{{3^3}}}\,;\,\,\frac{1}{{{3^4}}}\,;\,\,\frac{1}{{{3^5}}}\,; \cdots \] Số hạng tổng quát của dãy số này là
\({u_n} = \frac{1}{3} \cdot \frac{1}{{{3^{n\, + \,1}}}}.\)
\({u_n} = \frac{1}{{{3^{n\, + \,1}}}}.\)
\({u_n} = \frac{1}{{{3^n}}}.\)
\({u_n} = \frac{1}{{{3^{n\, - \,1}}}}.\)
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = - {n^2} + n + 1.\) Số \( - 19\) là số hạng thứ mấy của dãy?
5.
7.
6.
4.
Trong các dãy số sau đây, dãy số nào là một cấp số cộng?
\(1\,;\,\, - 2\,;\,\, - 4\,;\,\, - 6\,;\, - 8\,;\,\,\, \ldots \).
\(1\,;\,\, - 3\,;\,\, - 6\,;\,\, - 9\,;\, - 12\,;\,\,\, \ldots \).
\(1\,;\,\, - 3\,;\,\, - 7\,;\,\, - 11\,;\, - 15\,;\,\,\, \ldots \).
\(1\,;\,\, - 3\,;\,\, - 5\,;\,\, - 7\,;\, - 9\,;\,\,\, \ldots \).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 3\,;\,\,{u_8} = 24\) thì \({u_{11}}\) bằng
30.
33.
32.
28.
Trong các dãy số sau, dãy số nào là một cấp số nhân?
\[1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\, \ldots \].
\[2\,;\,\,4\,;\,\,6\,;\,\,8\,;\,\,16\,;\,\,32\,;\,\, \ldots \].
\[ - 2\,;\,\, - 3\,;\,\, - 4\,;\,\, - 5\,;\,\, - 6\,;\,\, - 7\,;\,\, \ldots \].
\[1\,;\,\,2\,;\,\,4\,;\,\,6\,;\,\,8\,;\,\,16\,;\,\,32\,;\,\, \ldots \].
Có bao nhiêu giá trị nguyên dương của \(x\) để ba số \(1\,;\,\,x\,;\,\,x + 2\) theo thứ tự đó lập thành cấp số nhân?
2.
1.
3.
0
Cho hình chóp \(S.ABC.\) Gọi \(M,\,\,N,\,\,K,\,\,E\) lần lượt là trung điểm của \(\)\(SA,\,\,SB,\,\,SC,\,\,BC.\) Bốn điểm nào sau đây đồng phẳng?
\(M,\,\,K,\,\,A,\,\,C\).
\(M,\,\,N,\,\,A,\,\,C\).
\(M,\,\,N,\,\,K,\,\,C\).
\(M,\,\,N,\,\,K,\,\,E\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,\,\,J\) lần luợt là trung điểm của \(SA\) và \(SB.\) Khẳng định nào sau đây sai?
\(IJCD\) là hình thang.
\(\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\)
\(\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\)
\(\left( {IAC} \right) \cap \left( {JBD} \right) = AO,\,\,O\) là tâm hình bình hành \(ABCD.\)
Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng sẽ
song song với hai đường thẳng đó.
song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
trùng với một trong hai đường thẳng đó.
cắt một trong hai đường thẳng đó.
Cho tứ diện \(ABCD.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AD\) và \(AC.\) Gọi \(G\) là trọng tâm tam giác \(BCD.\) Giao tuyến của hai mặt phẳng \(\left( {GMN} \right)\) và \(\left( {BCD} \right)\) là đường thẳng
qua \(M\) và song song với \(AB.\)
qua \(N\) và song song với \(BD.\)
qua \(G\) và song song với \(BC.\)
qua \(G\) và song song với \(CD.\)
II. Tự luận (4,0 điểm)
(1,0 điểm)Giải phương trình:
a) \(2\sin 2x + 1 = 0\); b) \(\tan \left( {\frac{{4\pi }}{9} + x} \right) + 2\cot \left( {\frac{\pi }{{18}} - x} \right) = \sqrt 3 \).
(0,5 điểm) Xét tính đơn điệu của dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{{5^n}}}{{{n^2}}}.\)
(1,5 điểm)Cho hình chóp \[S.ABCD\] có \[O\] là giao điểm của \[AC\] và \[BD.\] Một mặt phẳng \[\left( \alpha \right)\] cắt các cạnh \[SA,{\rm{ }}SB,{\rm{ }}SC,{\rm{ }}SD\] lần lượt tại \[A'\,,\,\,B'\,,\,\,C'\,,\,\,D'.\] Giả sử \[AB\] cắt \[CD\] tại \[E\] và \[A'B'\] cắt \[C'D'\] tại \[E'.\]
a) Chứng minh ba điểm\[S,{\rm{ }}E,{\rm{ }}E'\] thẳng hàng.
b) Tìm \[\left( {SAC} \right) \cap \left( {SBD} \right).\]
c) Chứng minh \[A'C',{\rm{ }}B'D',{\rm{ }}SO\] đồng quy.
(1,0 điểm)Tỉ lệ tăng dân số của tỉnh M là \(1,2\% \). Biết rằng số dân của tỉnh M hiện nay là 2 triệu người. Nếu lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
I. Trắc nghiệm (6 điểm)
Mệnh đề “\(\exists x \in \mathbb{R},{x^2} + 1 = 0\)” được phát biểu là
Tồn tại một số thực mà bình phương của nó cộng với 1 bằng 0;
Mọi số thực đều có bình phương của nó cộng với 1 bằng 0;
Tồn tại một số thực mà tổng của nó với 1 tất cả bình phương bằng 0;
Mọi số thực đều có tổng của nó với 1 tất cả bình phương bằng 0.
Cho mệnh đề \(P \Rightarrow Q\): “Nếu \({3^2} + 1\) là số chẵn thì 25 là số lẻ”. Khẳng định nào sau đây là đúng?
Mệnh đề \(Q \Rightarrow P\) là mệnh đề sai;
Cả hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều sai;
Mệnh đề \(P \Rightarrow Q\) là mệnh đề sai;
Cả hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng.
Cho tập hợp \[M = \left\{ {x \in \mathbb{Z}| - 4 < x \le 5} \right\}\]. Tập hợp \(M\) được viết dưới dạng liệt kê các phần tử là
\(M = \left\{ { - 4;\,\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\);
\(M = \left\{ {\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\);
\(M = \left\{ {\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\);
\(M = \left\{ { - 4;\,\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\).
Trong các khẳng định sau, khẳng định nào sai?
\(\emptyset \subset \mathbb{Z}\);
\(\mathbb{N} \subset \mathbb{Q}\);
\(\emptyset = \left\{ 0 \right\}\);
\(\emptyset \subset \mathbb{N}\).
Cho hai tập hợp: \(E = \left( { - 1;\,\,5} \right],F = \left[ {2;\,\,7} \right)\). Khi đó \(E \cap F\) là tập hợp nào sau đây?
\(\left( {2;\,\,5} \right]\);
\(\left( { - 1;\,\,2} \right]\);
\(\left[ {2;\,\,5} \right]\);
\(\left( {2;\,5} \right)\).
Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
\(4x + 13y > 1\,0\);
\(x + 9y \le 20\);
\({4^2}x + 9y \ge 15\);
\(4{x^2} + 9y < 10\).
Cặp số \(\left( {3;\,\,2} \right)\) là nghiệm của bất phương trình nào sau đây?
\(4x - 2x > 1\);
\(2x + 3y < 0\);
\(20x - y > 100\)
\(5x - y < 10\).
Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau?
\(\left\{ \begin{array}{l}2y > 3 - 5x\\x < 2\left( {4y + 1} \right)\end{array} \right.\); \(\left\{ \begin{array}{l}{x^2} + {y^2} > 2x\\x - y \le 15\end{array} \right.\); \(\left\{ \begin{array}{l}x\left( {x + y} \right) + y > 2\\x - 2\left( {y + 1} \right) \le 5\end{array} \right.\).
0;
1;
2;
3.
Bạn Hằng là du học sinh tại Hàn Quốc, vào mùa hè bạn ấy có hai công việc làm thêm là gia sư và thu ngân ở siêu thị. Mỗi giờ gia sư bạn được trả 12 000 won và mỗi giờ làm thu ngân ở siêu thị được trả 9 500 won. Gọi \(x\) là số giờ bạn Hằng làm gia sư và \(y\) là số giờ bạn ấy làm nhân viên thu ngân. Bạn ấy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số \(\left( {x;\,y} \right)\) nào sau đây thể hiện bạn Hằng kiếm được ít nhất 220 000 won mỗi tuần?
\(\left( {10;\,\,10} \right)\);
\(\left( {12;\,\,8} \right)\);
\(\left( {11;\,\,10} \right)\);
\(\left( {9;\,\,9} \right)\).
Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin \alpha = \sin \beta \);
\(\cos \alpha = - \cos \beta \);
\(\tan \alpha = - \tan \beta \);
\(\cot \alpha = \cot \beta \).
Cho tam giác \(ABC\) có \[BC = a,\,AC = b,\,AB = c\] và \(R\) là bán kính đường tròn ngoại tiếp tam giác. Công thức nào sau đây sai?
\(\frac{a}{{\sin A}} = 2R\);
\(\sin A = \frac{a}{{2R}}\);
\(b\sin B = 2R\);
\(\sin C = \frac{{c\sin A}}{a}\).
Tam giác \(ABC\) vuông cân tại \(A\) nội tiếp trong đường tròn tâm \(O\) bán kính \(R\) và có bán kính đường tròn nội tiếp tam giác là \(r\). Khi đó tỉ số \(\frac{R}{r}\) là
\(1 + \sqrt 2 \);
\(\frac{{2 + \sqrt 2 }}{2}\);
\(\frac{{\sqrt 2 - 1}}{2}\);
\(\frac{{1 + \sqrt 2 }}{2}\).
Hai vectơ được gọi là đối nhau khi
giá của chúng trùng nhau và độ dài của chúng bằng nhau;
chúng cùng hướng và độ dài của chúng bằng nhau;
chúng ngược hướng và độ dài của chúng bằng nhau;
chúng cùng phương và độ dài của chúng đối nhau.
Mệnh đề nào sau đây sai ?
\(\overrightarrow {AA} = \overrightarrow 0 \);
\(\overrightarrow 0 \) cùng phương với mọi vectơ;
\(\left| {\overrightarrow {AB} } \right| > 0\);
\(\overrightarrow 0 \) cùng hướng với mọi vectơ.
Cho hình chữ nhật \[ABCD\] tâm \(O\). Trong các mệnh đề sau, mệnh đề nào sai?
\[\overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BD} = \overrightarrow 0 \];
\[\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \];
\[\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \];
\[\overrightarrow {AD} - \overrightarrow {BC} = \overrightarrow 0 \].
Cho ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) cùng tác động vào một vật tại một điểm làm vật đứng yên (xem hình vẽ). Xét \(\overrightarrow {{F_4}} = \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \). Phát biểu nào sau đây là đúng?
\(\overrightarrow {{F_1}} = \overrightarrow {{F_4}} \);
\(\overrightarrow {{F_1}} = - \overrightarrow {{F_4}} \);
\(\overrightarrow {{F_1}} = \overrightarrow {{F_4}} + \overrightarrow {{F_2}} \);
\(\overrightarrow {{F_1}} = \overrightarrow {{F_4}} + \overrightarrow {{F_3}} \).
Cho đoạn thẳng \(AB\). Gọi \(M\) là một điểm trên \(AB\) sao cho \[AM = \frac{1}{4}AB\]. Khẳng định nào sau đây là sai?
\(\overrightarrow {MA} = \frac{1}{3}\overrightarrow {MB} \);
\(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} \);
\(\overrightarrow {BM} = \frac{3}{4}\overrightarrow {BA} \);
\(\overrightarrow {MB} = - 3\overrightarrow {MA} \).
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \), biết rằng hai vectơ \(\overrightarrow a ,\,\overrightarrow b \) ngược hướng và \(\left| {\overrightarrow a } \right| = 10,\,\,\left| {\overrightarrow b } \right| = 18\).
\(m = - \frac{5}{9}\);
\(m = - \frac{9}{5}\).
\(m = \frac{5}{9}\);
\(m = \frac{9}{5}\).
Cho hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) đều khác vectơ \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) > 90^\circ \). Khi đó ta có
\(\overrightarrow a \cdot \overrightarrow b < 0\);
\(\overrightarrow a \cdot \overrightarrow b = 0\);
\(\overrightarrow a \cdot \overrightarrow b > 0\);
\(\overrightarrow a \cdot \overrightarrow b \ge 0\).
Cho tam giác đều \[ABC\] cạnh bằng 5 và \(H\) là trung điểm của \(BC\). Khi đó, tích vô hướng \(\overrightarrow {AH} \cdot \overrightarrow {CA} \) bằng
\(\frac{{75}}{4}\);
\( - \frac{{75}}{4}\);
\(\frac{{75}}{2}\);
\( - \frac{{75}}{2}\).
II. Tự luận (4 điểm)
(1 điểm) Thống kê tại một trung tâm mua sắm gồm 47 cửa hàng, với 25 cửa hàng có bán quần áo, 17 cửa hàng có bán giày và 35 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:
a) Có bao nhiêu cửa hàng bán cả quần áo và giày?
b) Có bao nhiêu cửa hàng chỉ bán một trong hai loại quần áo hoặc giày?
c) Có bao nhiêu cửa hàng không bán cả hai loại hàng hóa trên?
(1 điểm) Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.
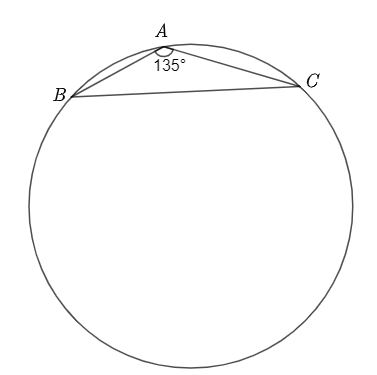
(1 điểm) Để đo đường kính của một hồ hình tròn, người ta làm như sau: Lấy ba điểm \(A,\,\,B,\,\,C\) như hình vẽ sao cho \(AB = 7,5\,\,{\rm{m}};\,\,AC = 10,5\,\,{\rm{m}};\,\widehat {BAC} = 135^\circ \). Hãy tính đường kính của hồ nước đó.
(1 điểm) Cho tam giác \[ABC\] có \[BC = a,\;CA = b,\;AB = c\].
a) Tính \[\overrightarrow {AB} \cdot \overrightarrow {AC} \]. Từ đó suy ra \[\overrightarrow {AB} \cdot \overrightarrow {BC} + \overrightarrow {BC} \cdot \overrightarrow {CA} + \overrightarrow {CA} \cdot \overrightarrow {AB} \].
b) Gọi \[G\] là trọng tâm tam giác \[ABC\]. Tính côsin của góc giữa hai vectơ \[\overrightarrow {AG} \] và \[\overrightarrow {BC} \].