Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 6
48 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Khẳng định nào sau đây là đúng khi nói về “góc lượng giác”?
Mỗi đường tròn là một đường tròn lượng giác.
Mỗi đường tròn có bán kính \(R = 1\) là một đường tròn lượng giác.
Mỗi đường tròn có bán kính \(R = 1\), tâm trùng với gốc tọa độ là một đường tròn lượng giác.
Mỗi đường tròn định hướng có bán kính \(R = 1\), tâm trùng với gốc tọa độ là một đường tròn lượng giác.
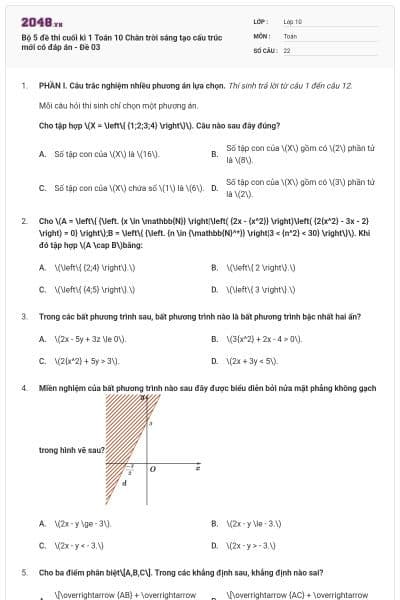
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác như hình vẽ bên dưới. Điểm \(M\) biểu diễn cho góc \(\alpha \) có số đo bằng bao nhiêu?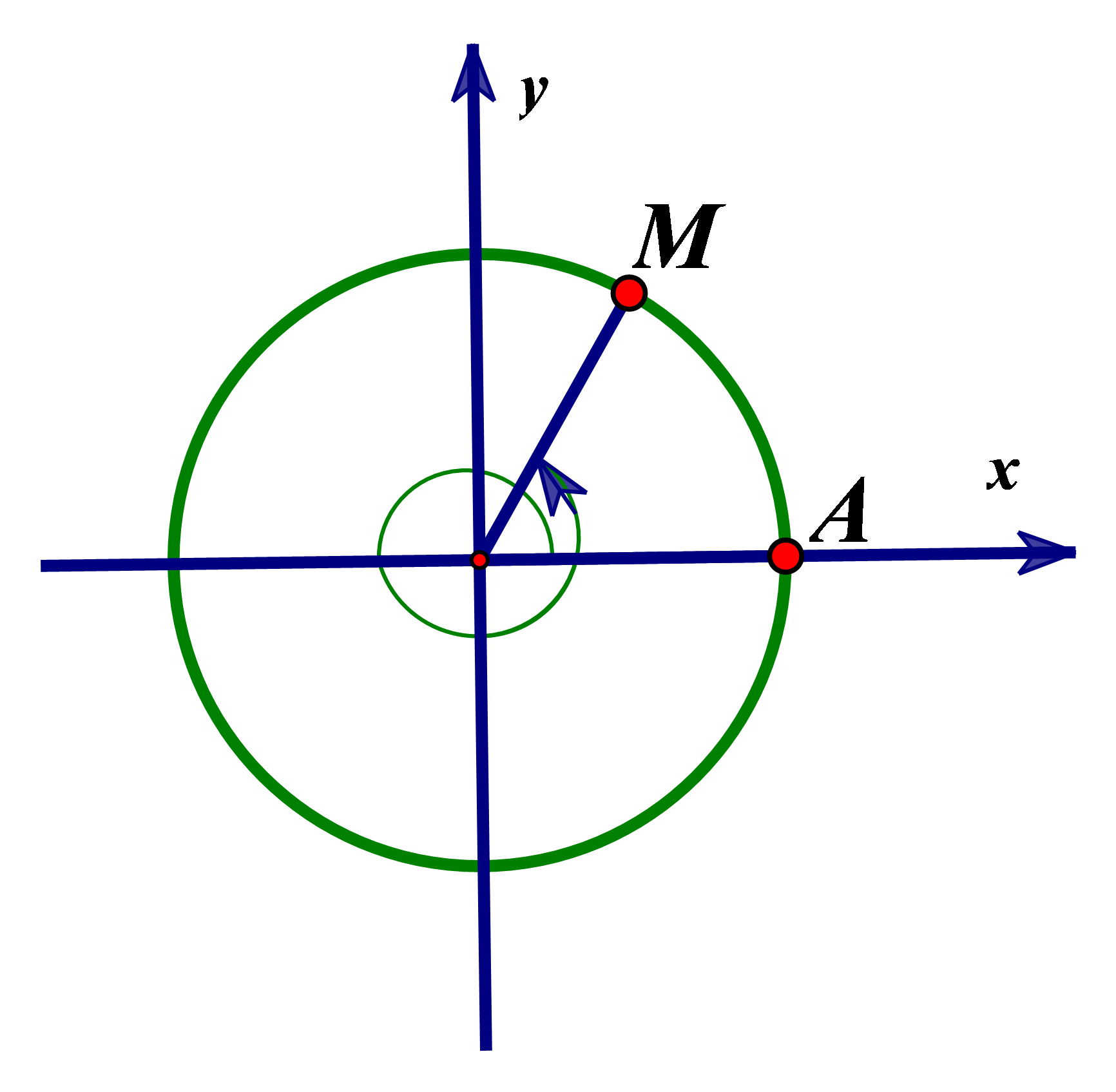
\(\alpha = 360^\circ .\)
\(\alpha = 390^\circ .\)
Cho \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây là đúng?
\(\sin \left( {\alpha - \pi } \right) \ge 0\).
\(\sin \left( {\alpha - \pi } \right) \le 0\).
\(\sin \left( {\alpha - \pi } \right) > 0\).
\(\sin \left( {\alpha - \pi } \right) < 0\).
Cho \[\tan \alpha = 3\]. Tính \[\tan \left( {\alpha - \frac{\pi }{3}} \right)\].
\[\frac{{3 - \sqrt 3 }}{{1 + 3\sqrt 3 }}\].
\[\frac{{3 + \sqrt 3 }}{{1 - 3\sqrt 3 }}\].
\[\frac{{1 - \sqrt 3 }}{{1 + 3\sqrt 3 }}\].
\[\frac{{1 - \sqrt 3 }}{{1 + \sqrt 3 }}\].
Khẳng định nào sai trong các khẳng định sau?
\({\sin ^2}x = \frac{{1 - \cos 2x}}{2}\).
\({\cos ^2}x = \frac{{1 + \cos 2x}}{2}\).
\[\sin x = 2\sin \frac{x}{2}\cos \frac{x}{2}\].
\(\cos 3x = {\cos ^3}x - {\sin ^3}x\).
Rút gọn biểu thức \(M = \frac{{\sin 3x - \sin x}}{{2{{\cos }^2}x - 1}}\).
\(\tan 2x.\)
\(\sin x.\)
\(2\sin x.\)
\(2\tan x.\)
Chọn mệnh đề đúng. Cho hàm số \(f\left( x \right) = \sin 2x\) và \(g\left( x \right) = {\tan ^2}x.\)
\(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số lẻ.
\(f\left( x \right)\) là hàm số lẻ, \(g\left( x \right)\) là hàm số chẵn.
\(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số chẵn.
\(f\left( x \right)\) và \(g\left( x \right)\) đều là hàm số lẻ.
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D.
Hỏi hàm số đó là hàm số nào?
\(y = \sin \frac{x}{2}.\)
\(y = \cos \frac{x}{2}.\)
\(y = \sin \left( { - \frac{x}{2}} \right).\)
\(y = - \cos \frac{x}{4}.\)
Tất cả nghiệm của phương trình \(\cos 2x = 0\) là
\(x = \frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}\).
\(x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
\(x = \pi + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Tất cả nghiệm của phương trình \(\sin \left( {x - \frac{\pi }{5}} \right) = \sin \frac{{2\pi }}{5}\) là
\(x = \frac{{3\pi }}{5} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{{2\pi }}{5} + k2\pi \) và \(x = \frac{{3\pi }}{5} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{{4\pi }}{5} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{{3\pi }}{5} + k2\pi \) và \(x = \frac{{4\pi }}{5} + k2\pi ,k \in \mathbb{Z}\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{ - n}}{{n + 1}}\). Năm số hạng đầu tiên của dãy số đó lần luột là số nào dưới đây?
\( - \frac{1}{2};\,\, - \frac{2}{3};\,\, - \frac{3}{4};\,\, - \frac{4}{5};\,\, - \frac{5}{6}.\)
\( - \frac{2}{3};\,\, - \frac{3}{4};\,\, - \frac{4}{5};\,\, - \frac{5}{6};\,\, - \frac{6}{7}.\)
\(\frac{1}{2};\,\,\frac{2}{3};\,\,\frac{3}{4};\,\,\frac{4}{5};\,\,\frac{5}{6}.\)
\(\frac{2}{3};\,\,\frac{3}{4};\,\,\frac{4}{5};\,\,\frac{5}{6};\,\,\frac{6}{7}.\)
Trong các dãy số \(\left( {{u_n}} \right)\)sau đây, dãy số nào là dãy số bị chặn?\(d = 8\)
\({u_n} = \sqrt {{n^2} + 1} \).
\({u_n} = n + \frac{1}{n}\).
\({u_n} = {2^n} + 1\).
\({u_n} = \frac{n}{{n + 1}}\).
Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số nào là một cấp số cộng?
\(0;\,\,1;\,\,3;\,\,7;\,\, \ldots \).
\(\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} - {u_n} = 2\end{array} \right.\,\,,\,\,\forall n \in \mathbb{N}*\).
\(1;\,\, - 1;\,\,1;\,\, - 1;\,\,1;\,\, \ldots \).
\({u_n} = {2^n},\,\,\forall n \in \mathbb{N}*\).
Cho cấp số cộng có công sai \(d\) bằng
\(d = 8\).
\(d = 7\).
\(d = 6\).
\(d = 5\).
Dãy số \(1\,;\,\,2\,;\,\,4\,;\,\,6\,;\,\,8\,;\,\, \ldots \) là một cấp số nhân với
Công bội là 3 và số hạng đầu tiên là 1.
Công bội là 2 và số hạng đầu tiên là 1.
Công bội là 4 và số hạng đầu tiên là 2.
Công bội là 2 và số hạng đầu tiên là 2.
Trong các dãy số \(\left( {{u_n}} \right)\) cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là một cấp số nhân?
\({u_n} = \frac{1}{{{3^{n\,\, - \,2}}}}\).
\({u_n} = \frac{1}{{{3^n}}} - 1\).
\({u_n} = n + \frac{1}{3}\).
\({u_n} = {n^2} - \frac{1}{3}.\)
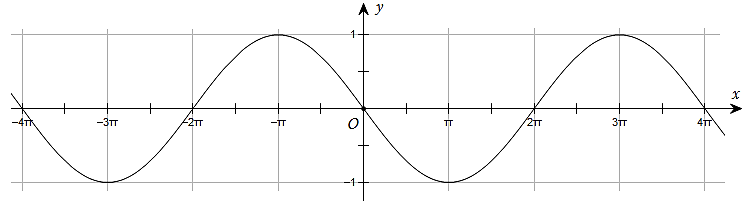
Trong các hình vẽ sau, hình nào có thể là hình biểu diễn của một hình tứ diện?
\((I)\).
\((I),\,\,(II),\,\,(IV)\).
\((I),\,\,(II),\,\,(III)\).
\((I),\,\,(II),\,\,(III),\,\,(IV)\).
Cho hình chóp \(S.ABCD\) có \(AC \cap BD = M\) và \(AB \cap CD = I.\)
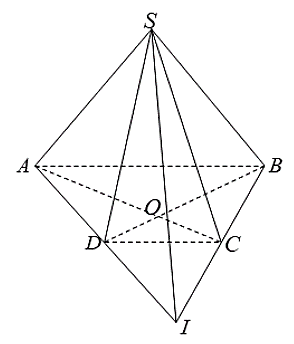
Giao tuyến của mặt phẳng \(\left( {SAB} \right)\) và mặt phẳng \(\left( {SCD} \right)\) là đường thẳng
\(SI\).
\(SA\).
\(MN\).
\(SM\).
Cho các mệnh đề sau:
(I) Hai đường thẳng song song thì đồng phẳng.
(II) Hai đường thẳng không có điểm chung thì chéo nhau.
(III) Hai đường thẳng chéo nhau thì không có điểm chung.
(IV) Hai đường thẳng chéo nhau thì không đồng phẳng.
Có bao nhiêu mệnh đề đúng?
1.
2.
3.
4.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(SA\) và \(SC\). Đường thẳng \(IJ\) song song với đường thẳng nào?
\(BC\) .
\(BD\).
\(SO\).
\(AC\).
II. Tự luận (4,0 điểm)
(1,0 điểm)Giải phương trình:
a) \(2\sin \left( {3x + \frac{\pi }{4}} \right) = \sqrt 3 \); b) \(\tan \left( {2x - \frac{\pi }{4}} \right) = \cot x\).
(0,5 điểm) Xét tính bị chặn của dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{4n + 5}}{{n + 1}}.\)
(1,5 điểm)Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là một tứ giác lồi. Gọi \[M\] là một điểm nằm trong \[\Delta SCD\].
a) Tìm \[\left( {SMB} \right) \cap \left( {SAC} \right)\].
b) Tìm \[BM \cap \left( {SAC} \right)\].
c) Tìm thiết diện hình chóp với \[\left( {ABM} \right).\]
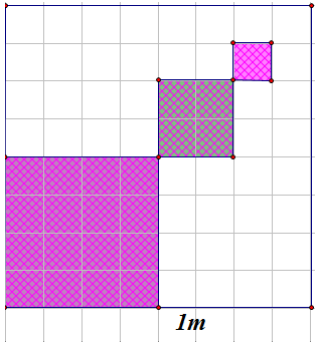
(1,0 điểm)Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 1 m. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là \(1;\,\,2;\,...;\,n,\) trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn \(\frac{1}{{1\,\,000}}\,\,{{\rm{m}}^{\rm{2}}}?\)
I. Trắc nghiệm (6 điểm)
Cho các câu sau:
(1) Số 23 là số nguyên tố.
(2) Số tự nhiên \(x\) là số chia hết cho 2.
(3) Em hãy học và làm bài tập chăm chỉ nhé!
(4) Tháng 2 dương lịch năm nhuận có 29 ngày.
Trong các câu trên, có bao nhiêu câu là mệnh đề?
1;
2;
3;
4.
Phủ định của mệnh đề “\(\exists x \in \mathbb{N},{x^2} - 5x > 1\)” là mệnh đề
“\(\exists x \in \mathbb{N},{x^2} - 5x \ne 1\)”;
“\(\forall x \in \mathbb{N},{x^2} - 5x < 1\)”;
“\(\forall x \in \mathbb{N},{x^2} - 5x \le 1\)”;
“\(\exists x \in \mathbb{N},{x^2} - 5x \ge 1\)”.
Phần không bị gạch trong hình vẽ bên mô tả tập hợp nào sau đây?
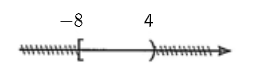
\(\left[ { - 8;\,\,4} \right)\);
\(\left[ { - 8;\,\,4} \right]\);
\(\left( { - 8;\,\,4} \right)\);
\(\left( { - 8;\,\,4} \right]\).
Trong các khẳng định sau, khẳng định nào sai?
\(8 \in \mathbb{Z}\);
\(\sqrt 7 \in \mathbb{Q}\);
\(0,567894 \in \mathbb{R}\);
\(\sqrt {16} \in \mathbb{N}\).
Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}| - 2 \le x < 9} \right\},B = \left( {2;\,\, + \infty } \right)\). Khi đó \({C_\mathbb{R}}\left( {A \cap B} \right)\) là tập hợp nào sau đây?
\(\left( { - \infty ;\,2} \right) \cup \left( {9;\, + \infty } \right)\);
\(\left[ { - 2;\,\, + \infty } \right)\);
\(\left( {2;\,\,9} \right)\);
\(\left( { - \infty ;\,2} \right] \cup \left[ {9;\, + \infty } \right)\).
Bạn Hằng muốn dùng 1 triệu đồng để mua \(x\) cốc trà sữa trân châu đường đen và \(y\) cái bánh pizza. Biết rằng mỗi cốc trà sữa trân châu đường đen có giá là 40 000 đồng và mỗi cái bánh pizza có giá là 139 000 đồng. Một bất phương trình mô tả điều kiện ràng buộc đối với \(x\) và \(y\) để Hằng không mua hết số tiền ban đầu là
\(40x + 139y > 1\,000\);
\(40x + 139y \le 1\,000\);
\(40x + 139y \ge 1\,000\);
\(40x + 139y < 1\,000\).
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(3x + 4y \ge 10\)?
\(\left( {0;\,\,2} \right)\);
\(\left( {3;\,\,0} \right)\);
\(\left( {1;\,\,2} \right)\)
\(\left( {1;\,\,1} \right)\).
Hệ bất phương trình nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x - 2y > 15\\x - 3y < 3\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} + y > 4\\x - 2y \le 5\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 4xy > 2\\2x - y < 7\end{array} \right.\);
\(\left\{ \begin{array}{l}3x + 5{y^2} < 2\\2x - 7y < 9\end{array} \right.\).
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 4\\x \ge 0\\y \ge 0\end{array} \right.\) là
Một nửa mặt phẳng;
Miền tam giác;
Miền tứ giác;
Miền ngũ giác.
Khẳng định nào sau đây là đúng?
\(\sin 120^\circ = - \frac{{\sqrt 3 }}{2}\);
\(\cos 120^\circ = \frac{{\sqrt 3 }}{2}\);
\(\tan 120^\circ = \sqrt 3 \);
\(\cot 120^\circ = - \frac{{\sqrt 3 }}{3}\).
Cho tam giác \(ABC\) có \[BC = a,\,AC = b,\,AB = c\] và \(\widehat A = 60^\circ \). Khi đó ta có công thức tính độ dài cạnh \(a\) là
\(a = \sqrt {{b^2} + {c^2} - bc} \);
\(a = \sqrt {{b^2} + {c^2} + bc} \);
\(a = b - c\);
\(a = c - b\).
Một mảnh đất hình tam giác có độ dài hai cạnh là \(AB = 10\,\,{\rm{m}},\,AC = 20\,\,{\rm{m}}\) và \(\widehat {BAC} = 150^\circ \). Diện tích mảnh đất là
100 m2;
50 m2;
173 m2;
137 m2.
Cho hai điểm \(A\), \(B\) phân biệt. Có tất cả bao nhiêu vectơ khác vectơ – không có được lập từ hai điểm này?
1;
2;
3;
4.
Cho vectơ \(\overrightarrow {MN} \) khác vectơ – không. Độ dài vectơ \(\overrightarrow {MN} \) là
Giá của vectơ \(\overrightarrow {MN} \);
Độ dài của đoạn thẳng \(MN\);
Phương của vectơ \(\overrightarrow {MN} \);
Hướng của vectơ \(\overrightarrow {MN} \).
Thực hiện phép tính \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} - \overrightarrow {CB} - \overrightarrow {FE} + \overrightarrow {DE} \) ta được kết quả là
\[\overrightarrow {AE} \];
\[\overrightarrow 0 \];
\[\overrightarrow {AF} \];
\[\overrightarrow {AD} \].
Cho tam giác \[ABC\] có \(M,\,\,N,\,\,P\) lần lượt là trung điểm các cạnh \(AB,\,\,AC,\,\,BC\). Vectơ \(\overrightarrow {MP} + \overrightarrow {NP} \) bằng vectơ nào sau đây?
\(\overrightarrow {AM} \);
\(\overrightarrow {PB} \);
\(\overrightarrow {AP} \);
\(\overrightarrow {MN} \).
Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \). Khẳng định nào sau đây là sai?
\(\overrightarrow a \) và \(6\overrightarrow a \) cùng phương;
\(\overrightarrow a \) và \( - 6\overrightarrow a \) cùng phương;
\(\overrightarrow a \) và \(6\overrightarrow a \) không cùng hướng;
\(\overrightarrow a \) và \( - 6\overrightarrow a \) ngược hướng.
Chotam giác \[ABC\] và điểm \(I\) sao cho \(\overrightarrow {IB} + 5\overrightarrow {IC} = \overrightarrow 0 \). Khẳng định nào sau đây là đúng?
\(\overrightarrow {AI} = \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \);
\(\overrightarrow {AI} = - \frac{1}{6}\overrightarrow {AB} - \frac{5}{6}\overrightarrow {AC} \).
\(\overrightarrow {AI} = - \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \);
\(\overrightarrow {AI} = \frac{1}{6}\overrightarrow {AB} - \frac{5}{6}\overrightarrow {AC} \).
Cho hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) đều khác vectơ \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) < 90^\circ \). Khi đó ta có
\(\overrightarrow a \cdot \overrightarrow b < 0\);
\(\overrightarrow a \cdot \overrightarrow b = 0\);
\(\overrightarrow a \cdot \overrightarrow b > 0\);
\(\overrightarrow a \cdot \overrightarrow b \ge 0\).
Cho hình vuông \[ABCD\] cạnh bằng 3. Gọi \(E\) là điểm đối xứng của \(D\) qua \(C\). Khi đó, tích vô hướng \(\overrightarrow {AE} \cdot \overrightarrow {AB} \) bằng
18;
\(9\sqrt 3 \);
\(9\sqrt 5 \);
45.
II. Tự luận (4 điểm)
(1 điểm) Cho các tập hợp khác tập rỗng \(A = \left[ {m - 1;\,\frac{{m + 3}}{2}} \right]\) và \(B = \left( { - \infty ;\,\, - 3} \right) \cup \left[ {3;\,\, + \infty } \right)\). Xác định các giá trị nguyên dương của \(m\) để \(A \cap B \ne \emptyset \).
(1 điểm) Một công ty dự kiến chi 500 triệu đồng cho một đợt quảng cáo sản phẩm của mình. Biết rằng chi phí cho một block 1 phút quảng cáo trên đài phát thanh là 10 triệu đồng và chi phí cho một block 10 giây quảng cáo trên đài truyền hình là 25 triệu đồng. Đài phát thanh chỉ nhận các chương trình quảng cáo với ít nhất 5 block, đài truyền hình chỉ nhận các chương trình quảng cáo với số block ít nhất là 10. Theo thống kê của công ty, sau 1 block quảng cáo trên đài truyền hình thì số sản phẩm bán ra tăng 4%, sau 1 block quảng cáo trên đài phát thanh thì số sản phẩm bán ra tăng 2%. Để đạt hiệu quả tối đa thì công ty đó cần quảng cáo bao nhiêu block trên đài phát thanh và trên đài truyền hình?
(1 điểm) Để đo chiều cao của một tòa nhà, bác Hương lấy hai điểm \(A\) và \(D\) trên mặt đất có khoảng cách \(AD = 10\,\,{\rm{m}}\) cùng thẳng hàng với chân \(B\) của tòa nhà để đặt hai giác kế. Chân của giác kế có chiều cao 1,2 m. Gọi \(C\) là đỉnh của tòa nhà và hai điểm \({A_1},\,\,{D_1}\) là đỉnh của hai giác kế cùng thẳng hàng với điểm \({B_1}\) thuộc chiều cao \(BC\) của tòa nhà. Bác đo được các góc \(\widehat {C{D_1}{B_1}} = 35^\circ ,\,\,\widehat {C{A_1}B} = 40^\circ \).
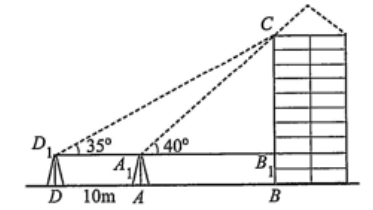
Hỏi chiều cao của tòa nhà là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
(1 điểm) Cho tam giác \[ABC\] có trực tâm \(H\). Gọi \(M\) là trung điểm của cạnh \(BC\). Chứng minh rằng \[\overrightarrow {MH} \cdot \overrightarrow {MA} = \frac{1}{4}B{C^2}\].