Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 5
76 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Quy ước chọn chiều dương của một đường tròn định hướng là
Luôn cùng chiều quay kim đồng hồ.
Luôn ngược chiều quay kim đồng hồ.
Có thể cùng chiều quay kim đồng hồ mà cũng có thể ngược chiều quay kim đồng hồ.
Không cùng chiều quay kim đồng hồ và cũng không ngược chiều quay kim đồng hồ.
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng \( - 405^\circ ?\)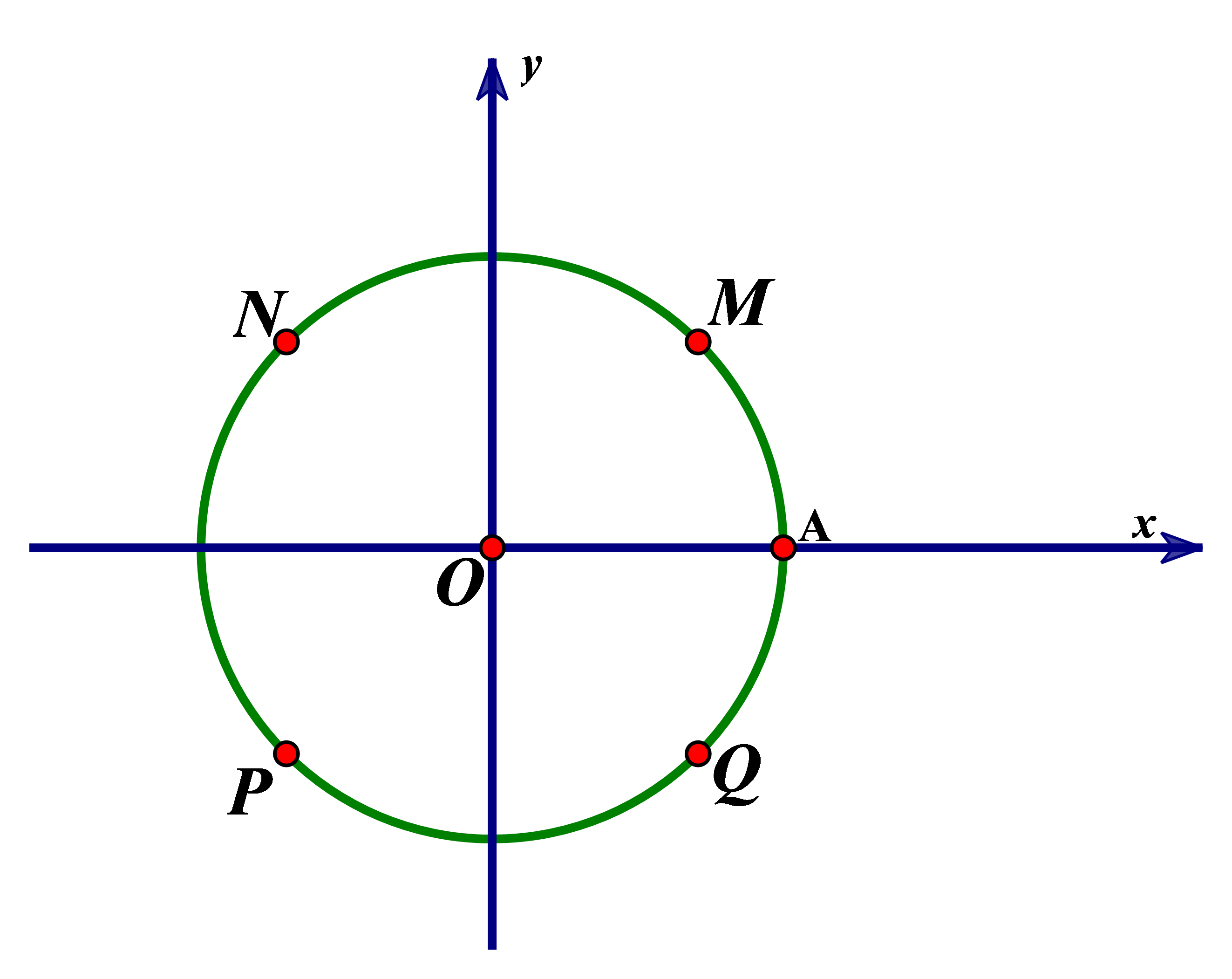
Điểm \(N.\)
Điểm \(M.\)
Điểm \(P.\)
Điểm \(P.\)
Đổi số đo của góc \(\alpha = \frac{\pi }{3}\) sang độ.
\(\alpha = 90^\circ .\)
\(\alpha = 30^\circ .\)
\(\alpha = 60^\circ .\)
\(\alpha = 45^\circ .\)
Cho \(2\pi < \alpha < \frac{{5\pi }}{2}\). Khẳng định nào sau đây là đúng?
\(\tan \alpha > 0,\,\,\cot \alpha > 0\).
\(\tan \alpha < 0,\,\,\cot \alpha < 0\).
\(\tan \alpha > 0,\,\,\cot \alpha < 0\).
\(\tan \alpha < 0,\,\,\cot \alpha > 0\).
Với mọi \(\alpha \in \mathbb{R}\) thì \(\tan (2017\pi + \alpha )\) bằng
\( - \tan x\).
\(\cot x\).
\(\tan x\).
\( - \cot x\).
Cho góc \(\alpha \) thỏa mãn \(\cos \alpha = - \frac{{\sqrt 5 }}{3}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khẳng định nào sau đây đúng?
\(\tan \alpha = - \frac{3}{{\sqrt 5 }}\).
\(\tan \alpha = \frac{2}{{\sqrt 5 }}\).
\(\tan \alpha = - \frac{4}{{\sqrt 5 }}\).
\(\tan \alpha = - \frac{2}{{\sqrt 5 }}\).
Khẳng định nào đúng trong các khẳng định sau?
\[\sin a + \cos a = \sqrt 2 \sin \left( {a - \frac{\pi }{4}} \right)\].
\[\sin a + \cos a = \sqrt 2 \sin \left( {a + \frac{\pi }{4}} \right)\].
\[\sin a + \cos a = - \sqrt 2 \sin \left( {a - \frac{\pi }{4}} \right)\].
\[\sin a + \cos a = - \sqrt 2 \sin \left( {a + \frac{\pi }{4}} \right)\].
Trong các mệnh đề sau, mệnh đề nào đúng?
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \cos x.cos\left( {x - \frac{\pi }{4}} \right).\)
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \sin x.cos\left( {x - \frac{\pi }{4}} \right).\)
\(1 + \sin 2x + \cos 2x = 2\cos x.\left( {\sin x - \cos x} \right).\)
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \cos x.cos\left( {x + \frac{\pi }{4}} \right).\)
Biến đổi biểu thức \[A = 4\sin x.\sin 2x.\sin 3x\] thành tổng, ta được
\[A = - \sin 4x + \cos 2x - \sin 6x\].
\[A = \sin 4x - \cos 2x - \sin 6x\].
\[A = \sin 4x - \sin 2x + \sin 6x\].
\[A = \sin 4x + \sin 2x - \sin 6x\].
Trong các hàm số sau, hàm số nào là hàm số chẵn?
\(y = \sin x.\)
\(y = \cos x.\)
\(y = \tan x.\)
\(y = \cot x.\)
Mệnh đề nào sau đây là sai?
Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \[y = \tan x\] tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi .\)
Tìm tập xác định \({\rm{D}}\) của hàm số \[y = \frac{{\cos x}}{{\sin \left( {x - \frac{\pi }{2}} \right)}}.\]
\[{\rm{D}} = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},\,k \in \mathbb{Z}} \right\}.\]
\[{\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,\,k \in \mathbb{Z}} \right\}.\]
\[{\rm{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\]
\[{\rm{D}} = \mathbb{R}\backslash \left\{ {\pi + 2k\pi ,\,k \in \mathbb{Z}} \right\}.\]
Nghiệm của phương trình \(\cos x = 1\) là
\(x = k\pi \).
\(x = \frac{\pi }{2} + k2\pi \).
\(x = k2\pi \).
\(x = \frac{\pi }{2} + k\pi \).
Tất cả nghiệm của phương trình \(\tan 2x = \tan \frac{\pi }{{11}}\) là
\(x = \frac{\pi }{{11}} + k\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{{22}} + k\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{{22}} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{{22}} + k\frac{\pi }{2},k \in \mathbb{Z}\).
Tất cả nghiệm của phương trình \(\sin 2x = \sin 3x\) là
\(x = \frac{\pi }{5} + k\frac{{2\pi }}{5},k \in \mathbb{Z}\).
\(x = k2\pi ,k \in \mathbb{Z}\).
\(x = k2\pi \) và \(x = \frac{\pi }{5} + k2\pi ,k \in \mathbb{Z}\).
\(x = k2\pi \) và \(x = \frac{\pi }{5} + k\frac{{2\pi }}{5},k \in \mathbb{Z}.\)
Tập nghiệm của phương trình \[2\sin 2x + 1 = 0\] là
\[S = \left\{ { - \frac{\pi }{{12}} + k\pi ,\,\,\frac{{7\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\].
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ,\,\, - \frac{{7\pi }}{{12}} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\[S = \left\{ { - \frac{\pi }{{12}} + k2\pi ,\,\,\frac{{7\pi }}{{12}} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\].
\(S = \left\{ { - \frac{\pi }{6} + k\pi ,\,\, - \frac{{7\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
Trong các dãy số \(\left( {{u_n}} \right)\) cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là dãy số tăng?
\[{u_n} = \frac{2}{{{3^n}}}\].
\[{u_n} = \frac{3}{n}\].
\[{u_n} = {2^n}\].
\[{u_n} = {\left( { - 2} \right)^n}\].
Mệnh đề nào sau đây đúng?
Dãy số \({u_n} = \frac{1}{n} - 2\) là dãy tăng.
Dãy số \[{u_n} = {( - 1)^n}\left( {{2^n} + 1} \right)\] là dãy giảm.
Dãy số \({u_n} = \frac{{n - 1}}{{n + 1}}\) là dãy giảm.
Dãy số \({u_n} = 2n + \cos \frac{1}{n}\) là dãy tăng.
Cho dãy số \(\left( {{u_n}} \right)\) biết \[{u_n} = \frac{{3n - 1}}{{3n + 1}}\]. Dãy số \(\left( {{u_n}} \right)\) bị chặn trên bởi số nào dưới đây?
\(\frac{1}{3}\).
1.
\(\frac{1}{2}\).
0.
Trong các dãy số sau, dãy số nào là một cấp số cộng?
\(1; - 2; - 4; - 6; - 8\).
\(1; - 3; - 6; - 9; - 12\).
\(1; - 3; - 7; - 11; - 15\).
\(1; - 3; - 5; - 7; - 9\).
Trong các dãy số sau, dãy số nào là một cấp số cộng?
\({u_n} = {( - 1)^n}(2n + 1)\).
\({u_n} = \sin \frac{\pi }{n}\).
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_n} = {u_{n - 1}} - 1\end{array} \right.\).
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_n} = 2{u_{n - 1}}\end{array} \right.\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = \frac{1}{4}\) và \(d = - \frac{1}{4}\). Gọi \({S_5}\) là tổng 5 số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào sau đây đúng?
\({S_5} = - \frac{4}{5}\).
\({S_5} = \frac{4}{5}\).
\({S_5} = \frac{5}{4}\).
\({S_5} = - \frac{5}{4}\).
Tổng \(n\) số hạng đầu tiên của một cấp số cộng là \({S_n} = {n^2} + 4n\) với \(n \in \mathbb{N}*\). Tìm số hạng tổng quát \({u_n}\) của cấp số cộng đã cho.
\({u_n} = 2n + 3\).
\({u_n} = 3n + 2\).
\({u_n} = 5\,.\,{3^{n - 1}}\).
\({u_n} = 5\,.\,{\left( {\frac{8}{5}} \right)^{n - 1}}\).
Cho các dãy số sau:
\((1):{u_n} = - \frac{{{3^{n - 1}}}}{5}\); \((2):{u_n} = 3n - 1\); \((3):{u_n} = \frac{{{2^n} - 1}}{3}\); \[(4):{u_n} = {n^3}\].
Hỏi có bao nhiêu dãy số là cấp số nhân?
1.
2.
3.
4.
Cho cấp số nhân \(\left( {{u_n}} \right)\) công bội \(q\). Mệnh đề nào sau đây đúng?
\[{u_k} = {u_1}{q^{k - 1}}\].
\[{u_k} = \frac{{{u_{k - 1}} + {u_{k + 1}}}}{2}\].
\[{u_k} = \sqrt {{u_{k + 1}}\,.\,{u_{k + 2}}} \].
\[{u_k} = {u_1} + (k - 1)q\].
Cho cấp số nhân \(\left( {{u_n}} \right)\) thỏa mãn \(\left\{ \begin{array}{l}{u_{20}} = 8{u_{17}}\\{u_1} + {u_5} = 272\end{array} \right.\). Chọn khẳng định đúng?
\(q = 2\).
\(q = - 4\).
\(q = 4\).
\(q = - 2\).
Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng các số hạng bằng 189. Tìm số hạng cuối \({u_6}\) của cấp số nhân đã cho.
\({u_6} = 32\).
\({u_6} = 104\).
\({u_6} = 48\).
\({u_6} = 96\).
Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
0.
2.
1.
vô số.
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Ba điểm phân biệt.
Một điểm và một đường thẳng.
Hai đường thẳng cắt nhau.
Bốn điểm phân biệt.
Cho tứ diện \[ABCD\]. Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(CD\). Mặt phẳng \((\alpha )\) qua \(MN\) cắt \(AD,\,\,BC\) lần lượt tại \(P\) và \(Q\). Biết \(MP\) cắt \(NQ\) tại \(I\). Ba điểm nào sau đây thẳng hàng?
\(I,\,\,A,\,\,C\).
\(I,\,\,B,\,\,D\).
\(I,\,\,A,\,\,B\).
\(I,\,\,C,\,\,D\).
Cho tứ diện \[ABCD\]. Gọi \[M,{\rm{ }}N\] lần lượt là các điểm thuộc \[AB,{\rm{ }}AC\]. Giao tuyến của hai mặt phẳng \[(DBN)\] và \((DCM)\) là
\[DG\] với \[G\] là trung điểm của \[BN\].
\[DG\] với \[G\] là giao điểm của \[BN\] và \[CM\].
\[DG\] với \[G\] là tâm đường tròn ngoại tiếp tam giác \[ABC\].
\[DG\] với \[G\] là trọng tâm tam giác \[ABC\].
Trong các mệnh đề sau, mệnh đề nào sai?
Hai đường thẳng chéo nhau thì không có điểm chung.
Hai đường thẳng không có điểm chung thì chéo nhau.
Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
Hai đường thẳng được gọi là song song nếu
chúng không có điểm chung.
chúng có một điểm chung duy nhất.
chúng đồng phẳng và không có điểm chung.
chúng đồng phẳng.
Cho hình chóp \(S.ABCD\) có \(AD\) không song song với \(BC\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,R,\,\,T\) lần lượt là trung điểm của \(AC,\,\,BD,\,\,BC,\,\,CD,\,\,SA,\,\,SD\). Cặp đường thẳng nào sau đây song song với nhau?
\(MP\)và \(RT\).
\(MQ\)và \(RT\).
\(MN\)và \(RT\).
\(PQ\)và \(RT\).
Cho tứ diện \(ABCD\). Các điểm \(P,\,\,Q\) lần lượt là trung điểm của \(AB\) và \(CD\); điểm \(R\) nằm trên cạnh \(BC\) sao cho \(BR = 2RC\). Gọi \(S\) là giao điểm của mặt phẳng \((PQR)\) và cạnh \(AD\). Tính tỉ số \(\frac{{SA}}{{SD}}\).
2.
1.
\(\frac{1}{2}\).
\(\frac{1}{3}\).
II. Tự luận (3,0 điểm)
(1,0 điểm)Giải phương trình:
a) \(\cot \left( {x + 30^\circ } \right) = \cot \frac{x}{2}\); b) \(\sin 2x = \cos 3x\).
(1,0 điểm) Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là \(12\,\,288\,\,{{\rm{m}}^{\rm{2}}}\)). Tính diện tích mặt trên cùng.
(1,0 điểm)Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AD\) và \(SB\).
a) Tìm giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\).
b) Chứng minh \(ON\) song song với mặt phẳng \[(SAD)\].
c) Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \((SAC)\).
I. Trắc nghiệm (7 điểm)
Mệnh đề “\(\exists x \in \mathbb{Z},x\,\, \vdots \,\,5\)” được diễn tả bằng lời là
Tồn tại một số nguyên \(x\) để \(x\) chia hết cho 5;
Mọi số nguyên \(x\) chia hết cho 5;
Tồn tại một số nguyên \(x\) để \(x\) không chia hết cho 5;
Mọi số nguyên \(x\) không chia hết cho 5.
Cho mệnh đề \(P\): “Tứ giác \(ABCD\) là hình thang cân” và mệnh đề \(Q\): “Tứ giác \(ABCD\) có \(AC = BD\)”. Mệnh đề \(P \Rightarrow Q\) được phát biểu là
Tứ giác \(ABCD\) là hình thang cân vì tứ giác \(ABCD\) có \(AC = BD\);
Nếu tứ giác \(ABCD\) là hình thang cân do đó tứ giác \(ABCD\) có \(AC = BD\); ;
Nếu tứ giác \(ABCD\) là hình thang cân thì tứ giác \(ABCD\) có \(AC = BD\);
Tứ giác \(ABCD\) có \(AC = BD\) khi và chỉ khi tứ giác \(ABCD\) là hình thang cân.
Cho định lí: “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ” để phát biểu lại định lí. Khẳng định nào sau đây là đúng ?
Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau;
Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau;
Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau;
Hai tam giác có diện tích bằng nhau là điều kiện cần và đủ để chúng bằng nhau.
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|{x^2} - 2x + 1 = 0} \right\}\). Trong các phần tử sau, phần tử nào thuộc tập hợp \(A\)?
1;
2;
– 1;
0.
Cho tập hợp \(B = \left\{ {x \in \mathbb{R}|5 < x < 50} \right\}\). Khoảng nào sau đây là tập con của \(B\) ?
\(\left( { - 1;6} \right)\)
\(\left( {45;69} \right)\);
\(\left( {23;34} \right)\);
\(\left( {1;50} \right)\).
Tập hợp số hữu tỉ được kí hiệu là
\(\mathbb{N}\);
\({\mathbb{N}^*}\);
\(\mathbb{Z}\);
\(\mathbb{Q}\).
Khẳng định nào sau đây là sai ?
\(\mathbb{N} = {\mathbb{N}^*}\);
\({\mathbb{N}^*} \subset \mathbb{N}\);
\(\mathbb{Z} \subset \mathbb{Q}\);
\(\mathbb{Q} \subset \mathbb{R}\).
Cho hai tập hợp \(A = \left[ {3;58} \right)\) và \(B = \left[ {1;5} \right]\). Khi đó tập hợp \(A \cup B\) là
\(\left[ {3;5} \right]\);
\(\left( {3;5} \right)\);
\(\left[ {1;3} \right]\);
\(\left[ {1;58} \right)\).
Bất phương trình nào dưới đây không phải là bất phương trình bậc nhất hai ẩn?
\(x - y \ge 8\);
\(3x + 7y < 0\);
\(4x > - 3\);
\(x - y + z < 1\).
Cặp số nào sau đây không là nghiệm của bất phương trình bậc nhất hai ẩn \(10x - y \ge 0\)?
\(\left( {3;\,2} \right)\);
\(\left( {1;\,\,11} \right)\);
\(\left( { - 1; - 14} \right)\);
\(\left( { - 2; - 20} \right)\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(3x - y \ge 1\) là
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\) (không kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) chứa điểm \(\left( {0;0} \right)\) (có kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\) (có kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\)(không kể bờ).
Trong các hệ bất phương trình sau, hệ bất phương trình bậc nhất hai ẩn là
\(\left\{ \begin{array}{l}{x^2} - {y^2} > 4\\2x + y < 1\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} - 2y \le z\\x + y < 9\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^5} - y > 0\\x + {y^5} < 6\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y - 3 > 4\\2x + y + 2 < 19\end{array} \right.\).
Cặp số nào sau đây là nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}5x - 2y \le 0\\x + y < 10\end{array} \right.\) ?
\(\left( {1;2} \right)\);
\(\left( {4;5} \right)\);
\(\left( {10;30} \right)\);
\(\left( { - 5;10} \right)\).
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \). Tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = \alpha \). Khi đó, giá trị \(\cos \alpha \) bằng
\(\frac{{AB}}{{AC}}\);
\(\frac{{AB}}{{BC}}\);
\(\frac{{AC}}{{BC}}\);
\(\frac{{AC}}{{AB}}\).
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \), \(\alpha \ne 90^\circ \), ta có: \[\tan \alpha = ?\]
\[\cot \left( {90^\circ - \alpha } \right)\];
\[\cot \left( {180^\circ - \alpha } \right)\];
\[\tan \left( { - \alpha } \right)\];
\[1 - \cot \left( \alpha \right)\].
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 90^\circ \) thỏa mãn \[\sin \alpha = \frac{1}{2}\]. Khi đó, giá trị \(\cot \alpha \) là
\(\frac{1}{{\sqrt 3 }}\);
\[\sqrt 3 \];
\(\frac{1}{2}\);
\(\frac{{\sqrt 3 }}{2}\).
Cho tam giác có độ dài ba cạnh lần lượt là \(a\), \(b\), \(c\), các góc đối diện các cạnh đó lần lượt là \(\alpha \), \(\beta \), \(\varphi \). Khẳng định nào sau đây là đúng ?
\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \varphi }}\);
\({a^2} = {b^2} - {c^2} - 2bc \cdot \cos \alpha \);
\({b^2} = {c^2} + {b^2} - 2ac \cdot \cos \beta \);
\({a^2} = {b^2} + {c^2} + 2bc \cdot \cos \alpha \).
Cho tam giác có độ dài ba cạnh lần lượt là \(a\), \(b\), \(c\), các góc đối diện các cạnh đó lần lượt là \(\alpha \), \(\beta \), \(\varphi \), các đường cao tương ứng lần lượt là \({h_a}\), \({h_b}\), \({h_c}\), diện tích tam giác đó là \(S\), nửa chu vi tam giác là \(p\). Khẳng định nào sau đây là sai ?
\(S = \frac{1}{2}a{h_a}\);
\(S = \frac{1}{2}b{h_a}\);
\(S = \frac{1}{2}ab.\sin \varphi \);
\[S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \].
Cho tam giác \(MNP\) có \(MN = 8\,\)cm, \(PN = 5\,\)cm, \(MP = 9\)cm. Vậy \(\widehat {MPN} = ?\) (làm tròn đến độ)
\(45^\circ \);
\(62^\circ \);
\(63^\circ \);
\(48^\circ \).
Cho tam giác \(ABC\) cân tại \(B\) có \(BC = 9\,\,{\rm{cm}}\), \(\widehat {ABC} = 38^\circ \). Làm tròn kết quả đến hàng đơn vị ta được độ dài cạnh \(AC\) là
6 cm;
9 cm;
8 cm;
7 cm.
Khẳng định nào sau đây là đúng ?
Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó;
Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi chưa biết yếu tố nào của tam giác đó;
Ta không thể vận dụng các định lí sin, định lí côsin để giải tam giác;
Ta không thể giải tam giác khi biết độ dài ba cạnh của tam giác đó.
Cho tam giác \(MNP\) có \(MN = 4\,\,{\rm{cm}}\), \(MP = 5\,\,{\rm{cm}}\), \(\widehat {MPN} = 45^\circ \). Làm tròn đến độ ta được số đo \(\widehat {MNP}\) bằng
\(62^\circ \);
\(63^\circ \);
\(64^\circ \);
\(65^\circ \).
Cho vectơ \(\overrightarrow {AB} \) khác vectơ – không, biết \(A\) và \(B\) nằm trên đường thẳng \(d\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} \) có điểm đầu là \(A\) và không có điểm cuối;
\(\overrightarrow {AB} \) có điểm đầu là \(A\) và điểm cuối là \(B\);
\(\overrightarrow {AB} \) có điểm đầu là \(B\) và điểm cuối là \(A\);
\(\overrightarrow {AB} \) có giá là đường thẳng vuông góc với đường thẳng \(d\).
Cho đoạn thẳng \(AB\) có trung điểm \(I\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} \) và \(\overrightarrow {BI} \) cùng hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {AI} \) cùng hướng;
\(\overrightarrow {AI} \) và \(\overrightarrow {IB} \) ngược hướng;
\(\overrightarrow {AI} \) và \(\overrightarrow {BI} \) không cùng phương.
Cho ba điểm \(A\), \(B\), \(C\) phân biệt. Ta có: \(\overrightarrow {AC} = ?\)
\(\overrightarrow {AB} - \overrightarrow {BC} \);
\(\overrightarrow {BC} - \overrightarrow {AB} \);
\(\overrightarrow {BC} + \overrightarrow {AB} \);
\(\overrightarrow {AB} + \overrightarrow {CB} \).
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} = \overrightarrow {CD} \);
\(\overrightarrow {AD} - \overrightarrow {BA} = \overrightarrow {AC} \);
\(\overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {BD} \);
\(\overrightarrow {AD} - \overrightarrow {AB} = \overrightarrow {AC} \).
Cho tam giác \(ABC\) vuông tại \(B\) có \(AB = 4\,\,{\rm{cm}}\), \(BC = 7\,\,{\rm{cm}}\). Tính độ dài vectơ \(\overrightarrow v = \overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {BA} \).
\(\sqrt {65} \,\,{\rm{cm}}\);
\(8\,\,{\rm{cm}}\);
\(\sqrt {66} \,\,{\rm{cm}}\);
\(7\,\,{\rm{cm}}\).
Cho ba điểm phân biệt \(A\), \(B\), \(C\), biết \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow 0 \). Khẳng định nào sau đây là đúng ?
\(A\) là trung điểm của đoạn thẳng \(BC\);
\(C\) không thuộc đường thẳng \(AB\);
\(B\) là trung điểm của đoạn thẳng \(AC\);
\(C\) ở giữa \(A\) và \(B\).
Cho vectơ \(\overrightarrow u \) khác vectơ – không. Tích của \(\overrightarrow u \) với số thực \(k > 0\) có thể nhận kết quả là
Một vectơ \(\overrightarrow v \) cùng hướng với \(\overrightarrow u \);
Một vectơ \(\overrightarrow v \) ngược hướng với \(\overrightarrow u \);
Một đoạn thẳng có độ dài bằng \(k\) lần độ dài của \(\overrightarrow u \);
Một số thực bằng \(k\) lần độ dài của \(\overrightarrow u \).
Cho hình thoi \(ABCD\) tâm \(O\), điểm \(M\) là trung điểm của \(OC\), ta có: \(\frac{1}{2}\overrightarrow {AO} = ?\)
\(\overrightarrow {MC} \);
\(\overrightarrow {CM} \);
\(\overrightarrow {OC} \);
\(\overrightarrow {AC} \).
Cho đoạn thẳng \(AB\) có điểm \(M\) sao cho \(AM = \frac{1}{5}AB\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} = \overrightarrow {AM} \);
\(\overrightarrow {AB} = \frac{4}{5}\overrightarrow {AM} \);
\(\overrightarrow {AM} = 4\overrightarrow {BM} \);
\(\overrightarrow {BA} = - 5\overrightarrow {AM} \).
Cho tam giác \(ABC\) và hai điểm \(M\), \(N\) lần lượt nằm trên hai cạnh \(AB\) và \(AC\) sao cho \(BM = \frac{1}{4}AB\) và \(AN = \frac{3}{4}AC\). Biểu diễn vectơ \(\overrightarrow {MN} \) theo hai vectơ \(\overrightarrow {AB} ,\,\overrightarrow {AC} \) ta được
\( - \frac{3}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \);
\(\frac{3}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \);
\( - \frac{3}{4}\overrightarrow {AB} - \frac{3}{4}\overrightarrow {AC} \);
\(\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \).
Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác vectơ – không, tích \(\overrightarrow u \cdot \overrightarrow v = 0\), nhận xét nào sau đây là đúng ?
\(\overrightarrow u \,\,{\rm{//}}\,\,\overrightarrow v \);
\(\overrightarrow u \) và \(\overrightarrow v \) cùng hướng;
\(\overrightarrow u \) và \(\overrightarrow v \) ngược hướng.
Cho tam giác \(ABC\) cân tại \(C\) cạnh \(AC = 5\,\,{\rm{cm}}\), \(\widehat {ACB} = 45^\circ \). Tính \(\overrightarrow {CA} \cdot \overrightarrow {CB} = ?\)
\(\frac{{25\sqrt 2 }}{2}\);
\( - \frac{{25\sqrt 2 }}{2}\);
\(\frac{{5\sqrt 2 }}{2}\);
\(25\sqrt 2 \).
Cho tam giác \(ABC\) có \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 2\sqrt 3 \) và \(AB = 2\), \(AC = 3\). Làm tròn đến độ ta được số đo của \(\widehat {BAC}\) là
\(55^\circ \);
\(54^\circ \);
\(56^\circ \);
\(57^\circ \).
II. Tự luận (3 điểm)
(1 điểm) Trong một cuộc thi làm bánh, mỗi đội chơi được sử dụng tối đa 20 kg bột mì, 2 kg bột nở, 5 kg kem béo. Để làm một cái bánh cỡ bé cần 0,4 kg bột mì, 0,05 kg bột nở và 0,1 kg kem béo; để làm một cái bánh cỡ trung bình 0,6 kg bột mì, 0,075 kg bột nở và 0,15 kg kem béo. Mỗi cái bánh cỡ bé được 5 điểm thưởng, mỗi cái bánh cỡ lớn được 7 điểm thưởng. Hỏi cần phải làm mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất?
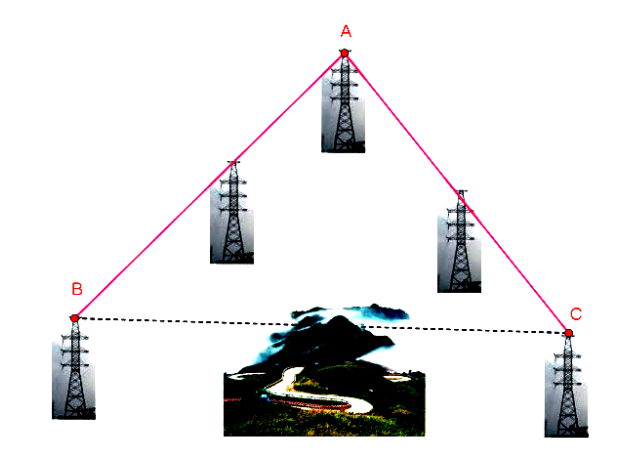
(1 điểm) Đường dây cao thế nối thẳng từ vị trí \(A\) đến vị trí \(B\) dài 15 km, từ vị trí \(A\) đến vị trí \(C\) dài 9 km, góc tạo bởi hai đường dây trên bằng \(86^\circ \). Tính khoảng cách từ vị trí \(B\) đến vị trí \(C\) (h.57). (làm tròn kết quả đến hàng phần trăm)
(1 điểm) Cho tam giác \(ABC\) có \(BC = a\), \(CA = b\), \(AB = c\) và \(M\) là trung điểm của \(BC\), \(AD\) là đường phân giác trong góc \(A\). Tính \({\overrightarrow {AD} ^2}\) theo \(a\), \(b\), \(c\).