Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 3
76 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Trong mặt phẳng tọa độ Oxy, đường tròn lượng giác là đường tròn
có tâm trùng với gốc tọa độ và bán kính bằng \(1.\)
có tâm trùng với gốc tọa độ.
bán kính bằng \(1.\)
có tâm trùng với gốc tọa độ và bán kính bằng \(2.\)
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác như hình vẽ, cho góc lượng giác có tia đầu là \(OA\) và số đo là \(135^\circ .\) Hỏi tia cuối của góc lượng giác đã cho là tia nào trong bốn đáp án A, B, C, D bên dưới?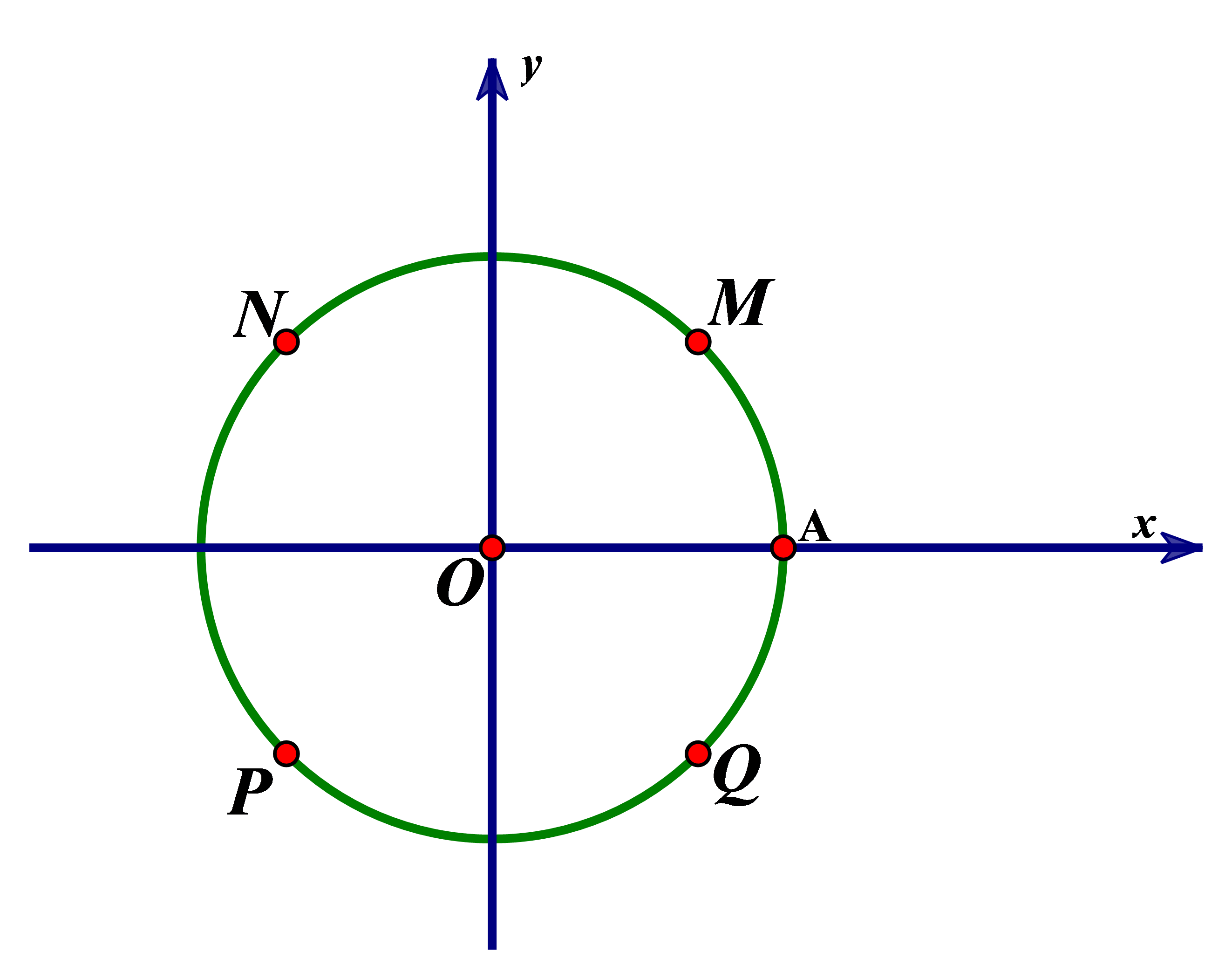
\(OQ.\)
\(OP.\)
\(OM.\)
\(ON.\)
Trên đường tròn lượng giác, góc lượng giác nào trong bốn đáp án A, B, C, D có điểm biểu diễn khác các góc còn lại.
\({\alpha _1} = 30^\circ .\)
\({\alpha _2} = 330^\circ .\)
\({\alpha _3} = 390^\circ .\)
\({\alpha _4} = - 330^\circ .\)
Điểm cuối của góc lượng giác\(\alpha \)ở góc phần phần tư thứ mấy nếu \(\sin \alpha ;\,\,\tan \alpha \) trái dấu?
Thứ I.
Thứ II hoặc IV.
Thứ II hoặc III.
Thứ I hoặc IV.
Để \(\tan x\) có nghĩa thì
\(x = \pm \frac{\pi }{2}\).
\(x = 0\).
\(x \ne \frac{\pi }{2} + k\pi \).
\(x \ne k\pi \).
Cho \(A,\,\,B,\,\,C\) là ba góc của một tam giác. Trong các hệ thức sau, hệ thức nào sai?
\(\sin A = - \sin \left( {2A + B + C} \right)\).
\(\sin A = - \cos \frac{{3A + B + C}}{2}\).
\(\cos C = \sin \frac{{A + B + 3C}}{2}\).
\(\sin C = \sin \left( {A + B + 2C} \right)\).
Trong các khẳng định sau, khẳng định nào sai?
\(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\).
\(\cos \left( {a - b} \right) = \cos a\cos b - \sin a\sin b\).
\(\sin \left( {a - b} \right) = \sin a\cos b - \cos a\sin b\).
\(2\cos a\cos b = \cos \left( {a - b} \right) + \cos \left( {a + b} \right)\).
Khẳng định nào dưới đây sai?
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\cos 2a = 2\cos a - 1\).
\(\sin 2a = 2\sin a\cos a\).
\(\sin \left( {a + b} \right) = \sin a\cos b + \sin b.\cos a\).
Cho \(\alpha ,\,\,\beta \) là hai góc nhọn thỏa mãn \(\tan \alpha = \frac{1}{7}\), \(\tan \beta = \frac{3}{4}\). Góc \(\alpha + \,\beta \) có giá trị bằng
\(\frac{\pi }{6}\).
\(\frac{\pi }{4}\).
\(\frac{\pi }{3}\).
\[\frac{\pi }{2}\].
Khẳng định nào sau đây đúng?
Hàm số \(y = {\rm{sin}}x\) là hàm số chẵn.
Hàm số \(y = {\rm{cos}}x\) là hàm số chẵn.
Hàm số \(y = {\rm{tan}}x\) là hàm số chẵn.
Hàm số \(y = {\rm{cot}}x\) là hàm số chẵn.
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \frac{{1 + \sin x}}{{\cos x - 1}}.\)
\({\rm{D}} = \mathbb{R}.\)
\({\rm{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
\({\rm{D}} = \mathbb{R}\backslash \left\{ {k2\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
Cho hàm số \[y = {\sin ^2}x + 2{\cos ^2}x\] liên tục trên \(\mathbb{R}\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho. Giá trị của \(M + 2m\) bằng
\(2\)
\(5\).
\(4\).
\(3\).
Trong các phương trình sau, phương trình tương đương với phương trình \({x^2} - 1 = 0\) là
\(x - 1 = 0\).
\(2{x^2} = 2\).
\({x^2} - 2 = 0\).
\({x^2} + 1 = 0\).
Tất cả nghiệm của phương trình \(\cos x = - \frac{{\sqrt 3 }}{2}\) là
\(x = \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = \frac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
\[x = \pm \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}\].
\(x = \pm \frac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
Tất cả nghiệm của phương trình \(\tan x = \sqrt 3 \) là
\(x = \frac{\pi }{3} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = \pm \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\).
\(x = \pm \frac{\pi }{3} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\).
Tất cả nghiệm của phương trình \(\cos \left( {3x + \frac{\pi }{4}} \right) = \cos \frac{\pi }{8}\) là
\(x = - \frac{\pi }{{24}} + k\frac{{2\pi }}{3},\,\,k \in \mathbb{Z}\).
\(x = \pm \frac{\pi }{{24}} + k\frac{{2\pi }}{3},\,\,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{8} + k2\pi \) và \(x = - \frac{{3\pi }}{8} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{{24}} + k\frac{{2\pi }}{3}\) và \(x = - \frac{\pi }{8} + k\frac{{2\pi }}{3},\,\,k \in \mathbb{Z}\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{ - \,n}}{{n + 1}}\). Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào?
\[ - \frac{1}{2};\,\, - \frac{2}{3};\,\, - \frac{3}{4};\,\, - \frac{4}{5}; - \frac{5}{6}\].
\[ - \frac{2}{3};\,\, - \frac{3}{4};\,\, - \frac{4}{5}; - \frac{5}{6}; - \frac{6}{7}\].
\[\frac{1}{2};\,\frac{2}{3};\,\,\frac{3}{4};\,\,\frac{4}{5};\,\,\frac{5}{6}\].
\[\frac{2}{3};\,\,\frac{3}{4};\,\,\frac{4}{5};\,\,\frac{5}{6};\,\,\frac{6}{7}\].
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát là \[{u_n} = 2\,.\,{3^n}\] với \(n \in \mathbb{N}*\). Công thức truy hồi của dãy số đó là
\[\left\{ \begin{array}{l}{u_1} = 6\\{u_n} = 6{u_{n - 1}},\,\,n > 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = 6\\{u_n} = 3{u_{n - 1}},\,\,n > 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = 3\\{u_n} = 3{u_{n - 1}},\,\,n > 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = 3\\{u_n} = 6{u_{n - 1}},\,\,n > 1\end{array} \right.\].
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \[\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right.\]. Tìm số hạng \({u_4}\).
\({u_4} = \frac{5}{9}\).
\({u_4} = 1\).
\({u_4} = \frac{2}{3}\).
\({u_4} = \frac{{14}}{{27}}\).
Cho cấp số cộng có \({u_1} = - \frac{1}{2};\,\,d = \frac{1}{2}\) thì dạng khai triển của cấp số cộng này là
\[ - \frac{1}{2};\,\,0;\,\,1;\,\,\frac{1}{2};\,\,1;\,...\].
\[ - \frac{1}{2};\,\,0;\,\,\frac{1}{2};\,\,0;\,\,\frac{1}{2};\,...\].
\[\frac{1}{2};\,\,1;\,\,\frac{3}{2};\,\,2\,;\,\,\frac{5}{2};\,...\].
\[ - \frac{1}{2};\,\,0;\,\,\frac{1}{2};\,\,1;\,\,\frac{3}{2};\,...\].
Cho cấp số cộng \(\left( {{u_n}} \right)\), biết \({u_n} = - 1;\,\,{u_{n + 1}} = 8\). Công sai của cấp số cộng đó là
\(d = - 9\).
\(d = 7\).
\(d = - 7\).
\(d = 9\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_2} = 2001\) và \({u_5} = 1995\). Khi đó \({u_{1001}}\) bằng
\({u_{1001}} = 4005\).
\({u_{1001}} = 4003\).
\({u_{1001}} = 3\).
\({u_{1001}} = 1\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa mãn \(\left\{ \begin{array}{l}{u_1} - {u_3} + {u_5} = 15\\{u_1} + {u_6} = 27\end{array} \right.\). Chọn khẳng định đúng trong các khẳng định sau.
\(\left\{ \begin{array}{l}{u_1} = 21\\d = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}{u_1} = 21\\d = - 3\end{array} \right.\).
\(\left\{ \begin{array}{l}{u_1} = 18\\d = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}{u_1} = 21\\d = 4\end{array} \right.\).
Dãy số nào sau đây là cấp số nhân?
\[\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + 1,\,\,n \ge 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = - 3{u_n},\,\,n \ge 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = - 2\\{u_{n + 1}} = 2{u_n} + 3,\,\,n \ge 1\end{array} \right.\].
\[\left\{ \begin{array}{l}{u_1} = - 1\\{u_n} = \sin \left( {\frac{\pi }{{n - 1}}} \right),\,\,n \ge 1\end{array} \right.\].
Cho dãy số \(\left( {{u_n}} \right)\) là một cấp số nhân với \[{u_n} \ne 0,\,\,n \in \mathbb{N}*\]. Dãy số nào sau đây không phải là cấp số nhân?
\[{u_1};\,\,{u_3};\,\,{u_5};...\].
\[3{u_1};\,\,3{u_2};\,\,3{u_3};...\].
\[\frac{1}{{{u_1}}};\,\,\frac{1}{{{u_2}}};\,\,\frac{1}{{{u_3}}};...\].
\[{u_1} + 2;\,\,{u_2} + 2;\,\,{u_3} + 2;...\].
Ba số hạng đầu của một cấp số nhân là \(x - 6;\,\,x\) và \(y\). Tìm \(y\), biết rằng công bội của cấp số nhân là 6.
\(y = 216\).
\(y = \frac{{324}}{5}\).
\(y = \frac{{1296}}{5}\).
\(y = 12\).
Cho cấp số nhân có số hạng lần lượt là \(1;\,\,4;\,\,16;\,\,64;\,\,...\) Gọi \({S_n}\) là tổng của cấp số nhân đó. Mệnh đề nào sau đây là đúng?
\({S_n} = {4^{n - 1}}\).
\({S_n} = \frac{{n\left( {1 + {4^{n - 1}}} \right)}}{2}\).
\[{S_n} = \frac{{{4^n} - 1}}{3}\].
\({S_n} = \frac{{4\left( {{4^n} - 1} \right)}}{3}\).
Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
6.
4.
3.
1.
Cho 3 đường thẳng \({d_1},\,\,{d_2},\,\,{d_3}\) không cùng một mặt phẳng và cắt nhau từng đôi một. Khẳng định nào sau đây đúng?
Ba đường thẳng trên đồng quy.
Ba đường thẳng trên trùng nhau.
Ba đường thẳng trên chứa ba cạnh của một tam giác.
Các khẳng định ở A, B, C đều sai.
Thiết diện của một tứ diện có thể là
tam giác.
tứ giác.
ngũ giác.
tam giác hoặc tứ giác.
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD\,\,(AB\,{\rm{//}}\,CD)\). Khẳng định nào sau đây là sai?
Hình chóp \(S.ABCD\) có 4 mặt bên.
Giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\) là \(SO\,\,(O\) là giao điểm của \(AC\) và \(BD).\)
Giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\) là \(SI\,\,(I\) là giao điểm của \(AD\) và \(BC).\)
Giao tuyến của hai mặt phẳng \((SAB)\) và \((SAD)\) là đường trung bình của \(ABCD\).
Trong các mệnh đề sau, mệnh đề nào đúng?
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng song song với nhau hoặc trùng nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt phẳng song song.
Cho ba mặt phẳng phân biệt \(\left( \alpha \right),\,\,\left( \beta \right),\,\,\left( \gamma \right)\) có \(\left( \alpha \right) \cap \,\left( \beta \right) = {d_1};\)\(\left( \beta \right) \cap \left( \gamma \right) = {d_2};\)\(\left( \alpha \right) \cap \left( \gamma \right) = {d_3}.\) Khi đó ba đường thẳng \({d_1},\,\,{d_2},\,\,{d_3}\)
đôi một cắt nhau.
đôi một song song.
đồng quy.
đôi một song song hoặc đồng quy.
Cho tứ diện \(ABCD\). Gọi \(I\) và \(J\) theo thứ tự là trung điểm của \(AD\) và \(AC,\,\,G\) là trọng tâm của tam giác \(BCD.\) Giao tuyến của hai mặt phẳng \((GIJ)\) và \((BCD)\) là đường thẳng
qua \(I\) và song song với \(AB\).
qua \(J\) và song song với \(BD\).
qua \(G\) và song song với \(CD\).
qua \(G\) và song song với \(BC\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I\) là trung điểm \(SA\). Thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \((IBC)\) là
tam giác \(IBC\).
hình thang \(IBCJ\,\,(J\) là trung điểm của \(SD\)).
hình thang \(IGBC\,\,(G\) là trung điểm của \(SB\)).
tứ giác \(IBCD\).
II. Tự luận (3,0 điểm)
(1,0 điểm)Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ \(t\) của năm 2017 được cho bởi một hàm số \(y = 4\sin \left[ {\frac{\pi }{{178}}(t - 60)} \right] + 10\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365.\) Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
(1,0 điểm) Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là \(80\,\,000\) đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng thêm \(5\,\,000\) đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống \[50\,\,m\] mới có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
(1,0 điểm)Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm của \(SO\). Mặt phẳng \((ICD)\) cắt \(SA,\,\,SB\) lần lượt tại \(M,\,\,N.\)
a) Nêu cách xác định hai điểm \(M\) và \(N\). Cho \(AB = a\). Tính \(MN\) theo \(a.\)
b) Trong mặt phẳng \((CDMN)\), gọi \(K\) là giao điểm của \(CN\) và \(DM\). Chứng minh \[SK\,{\rm{//}}\,BC\,{\rm{//}}\,AD\].
I. Trắc nghiệm (7 điểm)
Mệnh đề là
một câu cảm thán;
một khẳng định luôn đúng;
một câu nghi vấn hoặc câu cầu khiến;
một khẳng định chỉ có thể đúng hoặc sai.
Cách phát biểu nào sau đây không dùng để phát biểu định lí toán học dưới dạng \(P \Rightarrow Q\)?
Nếu \(P\) thì \(Q\);
\(P\) kéo theo \(Q\);
\(P\) là điều kiện cần để có \(Q\);
\(P\) là điều kiện đủ để có \(Q\).
Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\,2{x^2} + x + 1 > 0\)” là mệnh đề
“\(\forall x \in \mathbb{R},\,2{x^2} + x + 1 = 0\)”;
“\(\forall x \in \mathbb{R},\,2{x^2} + x + 1 \le 0\)”;
“\(\exists x \in \mathbb{R},\,2{x^2} + x + 1 < 0\)”;
“\(\exists x \in \mathbb{R},\,2{x^2} + x + 1 \le 0\)”.
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}|\left( {{x^2} - 1} \right)\left( {x - \frac{3}{2}} \right) = 0} \right\}\). Viết tập hợp \(A\) dưới dạng liệt kê các phần tử của tập hợp ta được
\(A = \left\{ {1;\,\,\frac{3}{2}} \right\}\);
\(A = \left\{ { - 1;\,\,1;\,\,\frac{3}{2}} \right\}\);
\(A = \left\{ { - 1;\,\,1} \right\}\);
\(A = \left\{ { - 1;\,\frac{3}{2}} \right\}\).
Cho tập \(Y = \left\{ {1;\,\,2;\,\,3} \right\}\). Khẳng định nào sau đây đúng?
Số tập con của \(Y\) là 16;
Số tập con của \(Y\) có 2 phần tử là 3;
Số tập con của \(Y\) chứa số 1 là 6;
Số tập con của \(Y\) chứa 3 phần tử là 0.
Chọn khẳng định sai trong các khẳng định sau:
\(\mathbb{N} \cap \mathbb{Z} = \mathbb{N}\);
\(\mathbb{Q} \cup \mathbb{R} = \mathbb{R}\);
\(\mathbb{Q} \cap {\mathbb{N}^*} = {\mathbb{N}^*}\);
\(\mathbb{Q} \cup {\mathbb{N}^*} = {\mathbb{N}^*}\).
Ký hiệu nào sau đây để chỉ 3 là số tự nhiên ?
\(3 \in \mathbb{N}\);
\(3 \notin \mathbb{N}\);
\(3 = \mathbb{N}\);
\(3 \subset \mathbb{N}\).
Cho hai tập hợp \(A = \left( {0;\,\,2} \right)\) và \(B = \left[ {1;\,\,4} \right)\). Tập hợp là
\(\left( { - \infty ;\,\,1} \right) \cup \left( {4;\, + \infty } \right)\);
\(\left( { - \infty ;\,0} \right) \cup \left( {4;\, + \infty } \right)\);
\(\left( { - \infty ;\,1} \right) \cup \left[ {2;\, + \infty } \right)\);
\(\left( { - \infty ;\,0} \right) \cup \left( {2;\, + \infty } \right)\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\( - x - 5{y^2} \ge 8\);
\({2^3}x - {3^2}y < 5\);
\(\frac{1}{x} - 2y < 0\);
\( - x + 3y = 0\).
Cặp số nào là một nghiệm của bất phương trình \( - 5x - y > 6\)?
\(\left( { - 1;\,\,1} \right)\);
\(\left( {1;\,\,3} \right)\);
\(\left( { - 3;\,\,0} \right)\);
\(\left( {4;\,\, - 2} \right)\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(2x - 5y \ge 3\) là
nửa mặt phẳng bờ là đường thẳng \(d:2x - 5y = 3\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:2x - 5y = 3\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
mửa mặt phẳng bờ là đường thẳng \(d:2x - 5y = 3\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:2x - 5y = 3\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\)).
Hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x \ge 5\\ - 3x + 5y < 9\end{array} \right.\);
\(\left\{ \begin{array}{l}{y^2} < - 2\\8x + y > - 1\end{array} \right.\);
\(\left\{ \begin{array}{l}3x + \frac{2}{y} > 2\\\frac{1}{x} + 3y > 6\end{array} \right.\);
\(\left\{ \begin{array}{l}2y\left( {x + y} \right) < 1\\x + 7y > 0\end{array} \right.\).
Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}2x + y \le 4\\ - 3x + 2y \ge - 5\end{array} \right.\) là phần mặt phẳng không bị gạch trong hình nào dưới đây?
A. 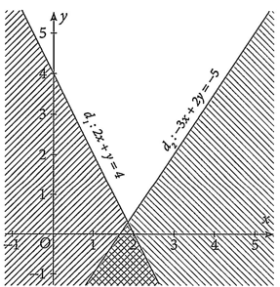 ;
;
B. 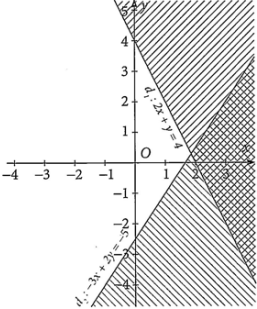 ;
;
C. 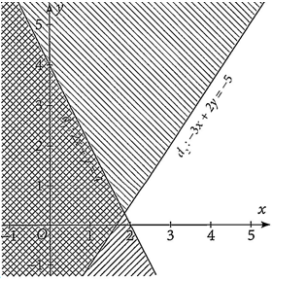 ;
;
D. 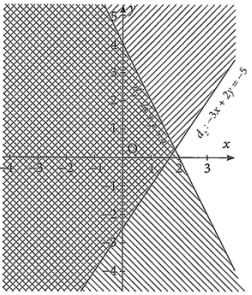 .
.
Cho góc nhọn alpha . Chọn khẳng định sai.
\[\sin \alpha > 0\];
\[\cos \alpha < 0\];
\[\tan \alpha > 0\];
\[\cot \alpha > 0\].
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{2}{3}\) và \(\cos \alpha < 0\). Số đo của góc \(\alpha \) thuộc khoảng nào sau đây?
\(\left( {0^\circ ;\,\,45^\circ } \right)\);
\(\left( {45^\circ ;\,\,90^\circ } \right)\);
\(\left( {45^\circ ;\,\,135^\circ } \right)\);
\(\left( {90^\circ ;\,180^\circ } \right)\).
Giá trị của biểu thức \(K = \sin 135^\circ \cdot \cos 60^\circ + \sin 60^\circ \cdot \cos 150^\circ \) là
\[\frac{{3 + \sqrt 2 }}{4}\];
\[\frac{{3 - \sqrt 2 }}{4}\];
\[\frac{{ - 3 + \sqrt 2 }}{4}\];
\[\frac{{ - 3 - \sqrt 2 }}{4}\].
Cho tam giác \(ABC\) với \(BC = a,\,\,AC = b,\,\,AB = c\); \(R\), \(r\) lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác; \(S\) là diện tích tam giác. Khẳng định nào sau đây là đúng?
\(S = \frac{{abc}}{{4r}}\);
\({a^2} = {b^2} + {c^2} + 2bc \cdot \cos A\);
\(R = \frac{a}{{\sin A}}\);
\(S = \frac{1}{2}ab\sin C\).
Diện tích \(S\) của tam giác \(ABC\) có \(AB = 2,\,AC = 7,\,\,\widehat A = 135^\circ \) bằng
\[\frac{{7\sqrt 2 }}{2}\];
\[7\sqrt 2 \];
\[\frac{{7\sqrt 2 }}{4}\];
\[\frac{{ - 7\sqrt 2 }}{2}\].
Cho tam giác \(ABC\) có \(\widehat A = 150^\circ ,\,\,BC = 24\). Bán kính đường tròn ngoại tiếp tam giác \(ABC\) bằng
24;
12;
48;
8.
Cho tam giác \(ABC\) có \(BC = 8,\,\,AC = 14,\,\,\widehat C = 120^\circ \). Độ dài cạnh \(AB\) là
\(3\sqrt {92} \);
\(2\sqrt {93} \);
\(2\sqrt {37} \);
\(3\sqrt {27} \).
Giải tam giác là
tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó;
tìm độ dài các cạnh của tam giác;
tìm số đo ba góc của tam giác;
tính diện tích tam giác bằng các cách khác nhau.
Cho tam giác \(ABC\) có \(BC = 16;\,\,\widehat B = 56^\circ ,\,\widehat C = 70^\circ \). Độ dài cạnh \(AC\) xấp xỉ bằng
16,4;
16,3;
16,2;
1\(6\),1.
Chọn khẳng định đúng.
Hai vectơ cùng hướng thì có giá song song;
Hai vectơ cùng phương thì có giá song song;
Hai vectơ cùng hướng thì cùng phương;
Hai vectơ cùng phương thì cùng hướng.
Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Diện tích;
Thể tích;
Giá tiền;
Lực.
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là sai?
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
\(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \);
\(\overrightarrow {AC} = \overrightarrow {BD} \);
\(\overrightarrow {AB} = \overrightarrow {DC} \).
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Đẳng thức nào sau đây là đúng?
\(\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {EO} = \overrightarrow 0 \);
\(\overrightarrow {BC} - \overrightarrow {FE} = \overrightarrow {AD} \);
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {EB} - \overrightarrow {OC} \);
\(\overrightarrow {AB} + \overrightarrow {CD} - \overrightarrow {FE} = \overrightarrow 0 \).
Cho hình chữ nhật \(ABCD\) có \(AB = 3a,\,\,AD = a\). Khi đó, \(\left| {\overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CD} } \right|\) bằng
\(a\sqrt {10} \);
\(4a\);
\(3a\);
\(5a\).
Cho điểm \(A\) cố định và vectơ \(\overrightarrow v \) khác vectơ-không. Có bao nhiêu điểm \(M\) thỏa mãn \(\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow v } \right|\)?
0;
1;
2;
Vô số.
Cho vectơ \(\overrightarrow a \) khác \(\overrightarrow 0 \) và một số thực \(k \ne 0\). Khẳng định nào sau đây là đúng?
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng phương;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng hướng;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) có độ dài bằng nhau;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn ngược hướng.
Cho hình thang \(MNPQ\) có \(MN\,{\rm{//}}\,PQ,\,MN = 2PQ\). Phát biểu nào sau đây là đúng?
\(\overrightarrow {MN} = 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = 2\overrightarrow {NP} \);
\(\overrightarrow {MN} = - 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = - 2\overrightarrow {NP} \).
Đẳng thức nào sau đây mô tả đúng hình vẽ dưới?

\(\overrightarrow {MP} = \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MP} = - \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MN} = 6\overrightarrow {MP} \);
\(\overrightarrow {MN} = 3\overrightarrow {PM} \).
Cho tam giác \[ABC\] và điểm \[I\] thỏa mãn \[\overrightarrow {IA} = - 2\overrightarrow {IB} \]. Biểu diễn \[\overrightarrow {IC} \] theo các vectơ \[\overrightarrow {AB} \], \[\overrightarrow {AC} \] ta được
\(\overrightarrow {IC} = - 2\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = 2\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = - \frac{2}{3}\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = \frac{2}{3}\overrightarrow {AB} + \overrightarrow {AC} \).
Cho tam giác \[ABC\]. Giá trị của biểu thức \(\overrightarrow {AB} \cdot \overrightarrow {AC} \) bằng
\(AB \cdot AC \cdot \cos A\);
\( - AB \cdot AC \cdot \cos A\);
\(AB \cdot AC \cdot \cos B\);
\(AB \cdot AC \cdot \cos C\).
Cho tam giác \[ABC\] cân tại \(A\) có \(\widehat A = 120^\circ \) và \(AB = a\). Tích vô hướng \(\overrightarrow {BA} \cdot \overrightarrow {CA} \) bằng
\(\frac{{{a^2}}}{2}\);
\( - \frac{{{a^2}}}{2}\);
\(\frac{{{a^2}\sqrt 3 }}{2}\);
\( - \frac{{{a^2}\sqrt 3 }}{2}\).
Cho tam giác \(ABC\) vuông tại \(A\) và có \(\widehat B = 50^\circ \). Hệ thức nào sau đây là sai?
\(\left( {\overrightarrow {AB} ,\,\overrightarrow {BC} } \right) = 130^\circ \);
\[\left( {\overrightarrow {BC} ,\,\overrightarrow {AC} } \right) = 40^\circ \];
\(\left( {\overrightarrow {AB} ,\,\overrightarrow {CB} } \right) = 50^\circ \);
\(\left( {\overrightarrow {AC} ,\,\overrightarrow {CB} } \right) = 120^\circ \).
II. Tự luận (3 điểm)
(1 điểm) Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24gam hương liệu, 9 lít nước và 210gam đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30gam đường, 1 lít nước và 1gam hương liệu; pha chế 1 lít nước táo cần 10gam đường, 1 lít nước và 4gam hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
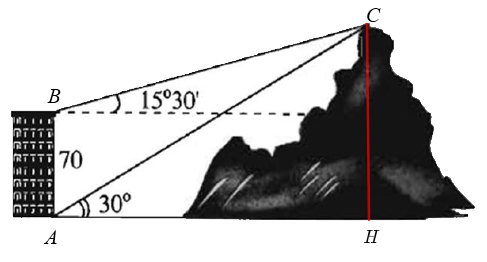
(1 điểm) Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB = 70\) m, phương nhìn \(AC\) tạo với phương nằm ngang góc \(30^\circ \), phương nhìn \(BC\) tạo với phương nằm ngang góc \(15^\circ 30'\). Tính chiều cao của ngọn núi (làm tròn đến hàng đơn vị).
(1 điểm) Cho tam giác \(ABC\) cân tại \(A\), \(H\) là trung điểm của \(BC\) và \(D\) là hình chiếu của \(H\) lên \(AC\), \(M\) là trung điểm của \(HD\). Chứng minh \[AM \bot BD\].