Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 1
76 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Cho hai tia \(Oa\) và \(Ob,\)hỏi tất cả có bao nhiêu góc lượng giác có tia đầu là \(Oa\) và tia cuối là \(Ob?\)
0
vô số.
\(2.\)
\(3.\)
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác như hình vẽ bên dưới. Góc lượng giác nào có số đo bằng \( - 45^\circ ?\)
\(\left( {OA,OM} \right).\)
\(\left( {OA,OQ} \right).\)
\(\left( {OA,ON} \right).\)
\(\left( {OA,OP} \right).\)
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác điểm gốc là \(A.\) Nếu góc lượng giác \(\left( {OA,OM} \right) = - \frac{{63\pi }}{2}\) thì \(OA\) và \(OM\)
vuông góc.
trùng nhau.
đối nhau.
tạo với nhau một góc \(\frac{\pi }{4}.\)
Cho \(\alpha \) thuộc góc phần phần tư thứ hai của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
\(\sin \alpha > 0;\,\,\cos \alpha > 0\).
\(\sin \alpha < 0;\,\,\cos \alpha < 0\).
\(\sin \alpha > 0;\,\,\cos \alpha < 0\).
\(\sin \alpha < 0;\,\,\cos \alpha > 0\).
Với mọi số thực \(\alpha \), ta có \(\sin \left( {\frac{{9\pi }}{2} + \alpha } \right)\) bằng
\( - \sin \alpha \).
\( - \cos \alpha .\)
\(\sin \alpha \).
\(\cos \alpha \).
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{{12}}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
\(\cos \alpha = \frac{1}{{13}}\).
\(\cos \alpha = \frac{5}{{13}}\).
\(\cos \alpha = - \frac{5}{{13}}\).
\(\cos \alpha = - \frac{1}{{13}}.\)
Chọn khẳng định đúng
\(\sin \left( {x + y} \right) = \sin x\cos y + \cos x\sin y\).
\(\cos \left( {x - y} \right) = \cos x\cos y - \sin x\sin y\).
\(\cos \left( {x + y} \right) = \cos x\cos y + \sin x\sin y\).
\(\sin \left( {x - y} \right) = \sin x\cos y + \cos x\sin y\).
Cho \[\sin x + \cos x = \frac{1}{2}\] và \[\frac{\pi }{2} < x < \pi \]. Giá trị của \(\sin \alpha \) là
\(\sin x = \frac{{1 + \sqrt 7 }}{6}\).
\(\sin x = \frac{{1 - \sqrt 7 }}{6}\).
\(\sin x = \frac{{1 + \sqrt 7 }}{4}\).
\(\sin x = \frac{{1 - \sqrt 7 }}{4}\).
Trong các mệnh đề sau, mệnh đề nào đúng?
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \cos x.cos\left( {x - \frac{\pi }{4}} \right).\)
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \sin x.cos\left( {x - \frac{\pi }{4}} \right).\)
\(1 + \sin 2x + \cos 2x = 2\cos x.\left( {\sin x - \cos x} \right).\)
\(1 + \sin 2x + \cos 2x = 2\sqrt 2 \cos x.cos\left( {x + \frac{\pi }{4}} \right).\)
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \frac{{2024}}{{\sin x}}.\)
\({\rm{D}} = \mathbb{R}.\)
\[{\rm{D}} = \mathbb{R}\backslash \left\{ 0 \right\}.\]
\[{\rm{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\]
\({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
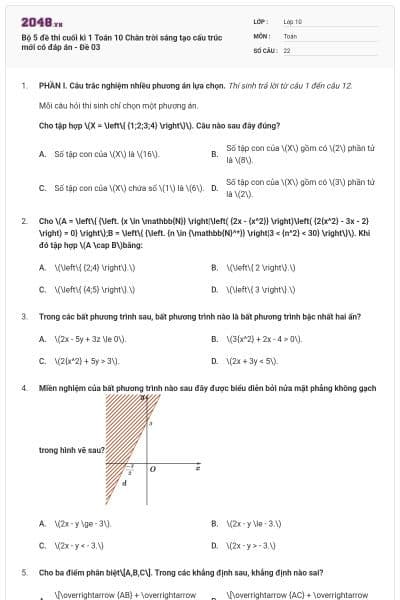
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D.
Hỏi hàm số đó là hàm số nào?
\[y = 1 + \sin 2x.\]
\[y = \cos x.\]
\[y = - \sin x.\]
\[y = - \cos x.\]
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu \(h\) (mét) của mực nước trong kênh được tính tại thời điểm \(t\) (giờ) trong một ngày bởi công thức \[h = 3\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 12.\] Mực nước của kênh cao nhất khi
\(t = 13\) (giờ).
\(t = 16\) (giờ).
\(t = 15\) (giờ).
\(t = 14\) (giờ).
Trong các phương trình sau, phương trình không tương đương với phương trình \({x^2} - 4 = 0\) là
\(2{x^2} = 8\).
\(\sqrt {2{x^2} - 4} = x\).
\[{x^2} - 4 + \frac{1}{{x - 3}} = \frac{1}{{x - 3}}\].
\(3{x^2} - 12 = 0\).
Tất cả nghiệm của phương trình \(\sin 2x = - \frac{3}{2}\) là
\(x = \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = \frac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{6} + k2\pi \) và \(x = \frac{{7\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}\).
Phương trình vô nghiệm.
Tất cả nghiệm của phương trình \(\cos 2x = \cos \left( {x + 60^\circ } \right)\) là
\(x = - 20^\circ + k120^\circ ,\,\,k \in \mathbb{Z}\).
\(x = 60^\circ + k360^\circ ,\,\,k \in \mathbb{Z}\).
\(x = 60^\circ + k360^\circ \) và \(x = - 20^\circ + k360^\circ ,\,\,k \in \mathbb{Z}\).
\(x = 60^\circ + k360^\circ \) và \(x = - 20^\circ + k120^\circ ,\,\,k \in \mathbb{Z}\).
Tại các giá trị nào của \(x\) thì đồ thị hàm số \(y = \cos x\) và \(y = \sin x\) giao nhau?
\(x = \frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}\).
\(x = \frac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}\).
\(x = \pm \frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}\).
\(x = \frac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}\).
Cho dãy số \[\left( {{u_n}} \right)\] với \[{u_n} = \frac{n}{{{3^n} - 1}}\]. Ba số hạng đầu tiên của dãy số lần lượt là.
\[\frac{1}{2};\frac{1}{4};\frac{3}{{27}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{26}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{25}}\].
\[\frac{1}{2};\frac{1}{4};\frac{3}{{28}}\].
Cho dãy số \[\left( {{u_n}} \right)\] được xác định bởi \[\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = {u_n} - 2\end{array} \right.,\forall n \in {\mathbb{N}^*}\]. Khẳng định nào sau đây đúng?
\(\left( {{u_n}} \right)\) là dãy số tăng.
\(\left( {{u_n}} \right)\) là dãy số giảm.
\(\left( {{u_n}} \right)\) không là dãy số tăng cũng không là dãy số giảm .
\(\left( {{u_n}} \right)\) là dãy số không đổi.
Cho dãy số \[\left( {{u_n}} \right)\] được xác định bởi \[\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = 3 + {u_n}\end{array} \right.,\forall n \in \left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\]. Tìm công thức số hạng tổng quát của \[\left( {{u_n}} \right)\].
\({u_n} = 3n - 1\) với \[n \in \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\].
\({u_n} = 3n - 1\) với \[n \in \left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\].
\({u_n} = {3^n}\) với \[n \in \left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\].
\({u_n} = {2^n}\) với \[n \in \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\].
Dãy số nào sau đây không phải là cấp số cộng?
\[ - \frac{2}{3};\,\, - \frac{1}{3};\,\,0;\,\,\frac{1}{3};\,\,\frac{2}{3};\,\,1;\,\,\frac{4}{3};...\].
\[15\sqrt 2 ;\,\,12\sqrt 2 ;\,\,9\sqrt 2 ;\,\,6\sqrt 2 ;...\].
\[\frac{4}{5};\,\,1;\,\,\frac{7}{5};\,\,\frac{9}{5};\,\,\frac{{11}}{5};...\].
\[\frac{1}{{\sqrt 3 }};\,\,\frac{{2\sqrt 3 }}{3};\,\,\sqrt 3 ;\,\,\frac{{4\sqrt 3 }}{3};\,\,\frac{5}{{\sqrt 3 }};...\].
Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
\({u_n} = {\left( { - 1} \right)^n}\left( {2n + 1} \right)\).
\({u_n} = \sin \frac{\pi }{n}\).
\(\left\{ \begin{array}{l}{u_n} = 1\\{u_n} = {u_{n - 1}} - 1\end{array} \right.\).
\(\left\{ \begin{array}{l}{u_n} = 1\\{u_n} = 2{u_{n - 1}}\end{array} \right..\)
Viết ba số hạng xen giữa các số \(2\) và \(22\) để được một cấp số cộng có năm số hạng.
\(7;\,\,12;\,\,17\).
\(6;\,\,10;\,\,14\).
\(8;\,\,13;\,\,18\).
\(6;\,\,12;\,\,18.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có các số hạng đầu lần lượt là \(5;\,\,9;\,\,13;\,\,17;...\). Tìm số hạng tổng quát \({u_n}\) của cấp số cộng.
\({u_n} = 5n + 1\).
\({u_n} = 5n - 1\).
\({u_n} = 4n + 1\).
\({u_n} = 4n - 1.\)
Dãy số nào sau đây không phải là cấp số nhân?
\[1;\,\,2;\,\,4;\,\,8;...\].
\[3;\,\,{3^2};\,\,{3^3};\,\,{3^4};...\].
\[4;\,\,2;\,\,\frac{1}{2};\,\,\frac{1}{4};...\].
\[\frac{1}{\pi };\,\,\frac{1}{{{\pi ^2}}};\,\,\frac{1}{{{\pi ^4}}};\,\,\frac{1}{{{\pi ^4}}};...\].
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{3}{2}\,.\,{5^n}\). Khẳng định nào sau đây đúng?
\(\left( {{u_n}} \right)\) không phải là cấp số nhân.
\(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = 5\) và số hạng đầu \({u_1} = \frac{3}{2}\).
\(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = 5\) và số hạng đầu \({u_1} = \frac{{15}}{2}\).
\(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = \frac{5}{2}\) và số hạng đầu \({u_1} = 3\).
Hai số hạng đầu của một cấp số nhân là \(2x + 1\) và \(4{x^2} - 1\). Số hạng thứ ba của cấp số nhân là
\(2x - 1\).
\(2x + 1\).
\(8{x^3} - 4{x^2} - 2x + 1\).
\(8{x^3} + 4{x^2} - 2x - 1\).
Một cấp số nhân có công bội bằng \(3\) và số hạng đầu bằng \(5\). Biết số hạng chính giữa là \(32\,\,805\). Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
\(18\).
\(17\).
\(16\).
\(9\).
Trong các mệnh đề sau đây, mệnh đề nào sai?
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng cùng đi qua ba điểm \(A,\,\,B,\,\,C\) không thẳng hàng thì mặt phẳng đó trùng nhau.
Cho tứ giác \(ABCD\). Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của giác giác \(ABCD\)?
\(1\).
\(2\).
\(3\).
\(0\).
Cho điểm \(A\) không nằm trên mặt phẳng \((\alpha )\) chứa tam giác \(BCD\). Lấy \(E,\,\,F\) là các điểm lần lượt nằm trên các cạnh \(AB,\,\,AC\). Khi \(EF\) và \(BC\) cắt nhau tại \(I\) thì \(I\) không phải là điểm chung của hai mặt phẳng nào sau đây?
\[(BCD)\] và \[(DEF)\].
\[(BCD)\] và \[(ABC)\].
\[(BCD)\] và \[(AEF)\].
\[(BCD)\] và \[(ABD)\].
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD\,\,(AD\,{\rm{//}}\,BC)\). Gọi \(M\) là trung điểm của \(CD\). Giao tuyến của hai mặt phẳng \((MSB)\) và \((SAC)\) là
\(SI\,\,(I\)là giao điểm của \(AC\) và \(BM)\).
\(SJ\,\,(J\)là giao điểm của \(AM\) và \(BD)\).
\(SO\,\,(O\)là giao điểm của \(AC\) và \(BD)\).
\(SP\,\,(P\)là giao điểm của \(AB\) và \(CD)\).
Trong các mệnh đề sau, mệnh đề nào sai?
Hai đường thẳng không có điểm chung thì chéo nhau.
Hai đường thẳng chéo nhau thì không có điểm chung.
Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
Hai đường thẳng phân biệt không chéo nhau thì cắt nhau hoặc song song.
Cho hai đường thẳng chéo nhau \(a,\,\,b\) và điểm \(M\) ở ngoài \(a\) và ngoài \(b\). Có nhiều nhất bao nhiêu đường thẳng qua \(M\) cắt cả \(a\) và \(b\)?
\(1\).
\(2\).
\(0\).
Vô số.
Cho tứ diện \(ABCD\). Gọi \(M,\,\,N\) là hai điểm phân biệt cùng thuộc đường thẳng \(AB;\,\,P,\,\,Q\) là hai điểm phân biệt cùng thuộc đường thẳng \(CD\). Vị trí tương đối của hai đường thẳng \[MP,\,\,NQ\] là
\[MP\,{\rm{//}}\,NQ\].
\[MP \equiv NQ\].
\[MP\] cắt \[NQ\].
\[MP,\,\,NQ\] chéo nhau.
Cho tứ diện \(ABCD\), \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\). Mặt phẳng \((\alpha )\) qua \(MN\) cắt tứ diện \(ABCD\) theo thiết diện là đa giác \((T)\). Khẳng định nào sau đây đúng?
\((T)\) là hình chữ nhật.
\((T)\) là hình tam giác.
\((T)\) là hình thoi.
\((T)\) là hình tam giác; hình thang hoặc hình bình hành.
II. Tự luận (3,0 điểm)
(1,0 điểm) Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức:
\(h(t) = 29 + 3\sin \frac{\pi }{{12}}(t - 9)\),
với \(h\) tính bằng độ \(C\) và \(t\) là thời gian trong ngày tính bằng giờ.
(Theo https://www.sciencedirect.com//science/articlelabs//pii/0168192385900139)
Nhiệt độ thấp nhất trong ngày là bao nhiêu độ \(C\) và vào lúc mấy giờ?
(1,0 điểm) Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 giờ, sau mỗi giờ thì số tiếng chuông được đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một ngày đồng hồ đó đánh bao nhiêu tiếng chuông?
(1,0 điểm)Cho tứ diện \(ABCD\). Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(BC\) và \(AC\). Trên cạnh \(PD\) lấy điểm \(P\) sao cho \(DP = 2PB\).
a) Xác định giao tuyến của mặt phẳng \((MNP)\) với các mặt phẳng \((ABD),\,\,(BCD).\)
b) Trên cạnh \(AD\) lấy điểm \(Q\) sao \(DQ = 2QA\). Chứng minh: \(PQ\) song song với mặt phẳng \((ABC)\), ba đường thẳng \(DC,\,\,QN,\,\,PM\) đồng quy.
I. Trắc nghiệm (7 điểm)
Trong các câu sau, câu nào không phải là mệnh đề?
“Tam giác có hai cạnh bằng nhau là tam giác cân.”;
“Số 100 là một hợp số.”;
“Số 2 022 có chia hết cho 4 không?”;
“Phương trình bậc nhất luông có nghiệm.”.
Mệnh đề “\(\exists x \in \mathbb{N},\,{x^2} = 10\)” khẳng định rằng
Bình phương của một số tự nhiên bằng 10;
Bình phương của một số \(x\) bằng 10;
Chỉ có một số tự nhiên mà bình phương của nó bằng 10;
Có ít nhất một số tự nhiên mà bình phương của nó bằng 10.
Phủ định của mệnh đề “Bất phương trình \(2{x^2} + 3 > 1\) vô nghiệm” là mệnh đề
“Bất phương trình \(2{x^2} + 3 > 1\) không có nghiệm”;
“Bất phương trình \(2{x^2} + 3 > 1\) có nghiệm”;
“Bất phương trình \(2{x^2} + 3 < 1\) vô nghiệm”;
“Bất phương trình \(2{x^2} + 3 < 1\) có nghiệm”.
Viết tập hợp A: “tập hợp các số thực lớn hơn 2 và nhỏ hơn 5” dưới dạng nêu tính chất đặc trưng cho phần tử của tập hợp, ta được
\(A = \left\{ {x \in \mathbb{R}|\,2 \le x \le 5} \right\}\);
\(A = \left\{ {2;\,\,5} \right\}\);
\(A = \left\{ {x \in \mathbb{R}|\,2 < x < 5} \right\}\);
\(A = \left\{ {x \in \mathbb{Z}|\,2 < x < 5} \right\}\).
Cho tập hợp \(B = \left\{ {1;\,\,3;\,\,5;\,\,7;\,\,9} \right\}\). Tập hợp nào sau đây là tập con của tập \(B\)?
\({B_1} = \left\{ {1;\,\,3;\,\,5;\,\,11} \right\}\);
\({B_2} = \left\{ {1;\,\,2;\,\,3;\,\,5;\,\,9} \right\}\);
\({B_3} = \left\{ {1;\,\,3;\,\,7;\,\,9} \right\}\);
\({B_1} = \left\{ {1;\,\,3;\,\,5;\,\,10} \right\}\).
Khẳng định nào sau đây là sai?
\(\mathbb{N}\) là tập hợp các số tự nhiên;
\(\mathbb{Z}\) là tập hợp các số nguyên;
\(\mathbb{Q}\) là tập hợp các số vô tỉ;
\(\mathbb{R}\) là tập hợp các số thực.
Khẳng định nào sau đây là đúng?
\(\mathbb{N} \in \mathbb{Z}\);
\(\mathbb{Q} \subset \mathbb{Z}\);
\(\mathbb{Q} \subset \mathbb{R}\);
\({\mathbb{N}^*} \in \mathbb{N}\).
Cho hai tập hợp \(A = \left[ { - 2;\,\,5} \right)\) và \(B = \left[ {0;\,\, + \infty } \right)\). Tập hợp \(A \cup B\) là
\(\left[ { - 2;\, + \infty } \right)\);
\(\left[ { - 2;\,\,0} \right)\);
\(\left[ {0;\,\,5} \right)\);
\(\left[ {5;\,\, + \infty } \right)\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(2x - 4y \ge 7\);
\(5{x^3} - 4{y^3} < 2\);
\({x^2} - 2y < 0\);
\({x^2} + 3 > 0\).
Cặp số nào là nghiệm của bất phương trình \(2x + 3y \ge 6\)?
\(\left( {1;\,\, - 3} \right)\);
\(\left( { - 3;\,\, - 4} \right)\);
\(\left( {7;\,\,8} \right)\);
\(\left( { - 1;\,\, - 2} \right)\).
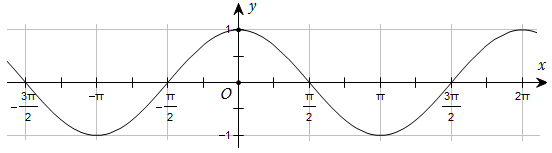
Nửa mặt phẳng không bị gạch trong hình bên (bao gồm cả đường thẳng \(d\)) là miền nghiệm của bất phương trình nào trong các bất phương trình sau?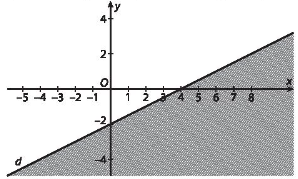
\(x - 2y \ge 4\);
\(x - 2y > 4\);
\(x - 2y < 4\);
\(x - 2y \le 4\).
Trong các hệ bất phương trình sau, đâu là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y - 5 \ge 0\\x - {y^2} > 0\end{array} \right.\);
\(\left\{ \begin{array}{l}2x + y - 1 < 0\\x - 2y > 0\\x + 5y = 4\end{array} \right.\);
\(\left\{ \begin{array}{l}3x + 2y = 2\\3x - y < 0\\x - y > 0\end{array} \right.\);
\(\left\{ \begin{array}{l}7x - y < 1\\x + 6y > 0\\4x + 5y \le 0\end{array} \right.\).
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 15 < 0\\x + y > 0\end{array} \right.\) chứa điểm nào trong các điểm sau đây?
\[\left( {1;\,\,15} \right)\];
\[\left( {1;\,\,2} \right)\];
\[\left( {9;\,\,11} \right)\];
\[\left( {7;\,\,8} \right)\].
Với giá trị nào của \(\alpha \) thì \(\cos \alpha > 0\)?
\[0^\circ < \alpha \le 90^\circ \];
\[90^\circ < \alpha \le 180^\circ \];
\[0^\circ \le \alpha \le 90^\circ \];
\[0^\circ \le \alpha < 90^\circ \].
Chọn khẳng định đúng trong các khẳng định sau.
\(\sin 150^\circ = \sin 30^\circ \);
\(\sin 150^\circ = - \sin 30^\circ \);
\(\tan 150^\circ = \tan 30^\circ \);
\(\cot 150^\circ = \cot 30^\circ \).
Giá trị của \(\sin 45^\circ + \cos 45^\circ \) là
\[\frac{{\sqrt 2 }}{2}\];
1;
\[\sqrt 2 \];
\[2\sqrt 2 \].
Cho tam giác \(ABC\) có \(\widehat A = 60^\circ \). Diện tích tam giác \(ABC\) là
\(\frac{{\sqrt 2 }}{4}AB \cdot AC\);
\(\frac{{\sqrt 3 }}{2}BC \cdot AC\);
\( - \frac{1}{2}AB \cdot AC\);
\(\frac{1}{2}AB \cdot AC\).
Cho tam giác \(ABC\) có \(BC = a,\,AC = b,\,AB = c\) và \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\). Trong các công thức dưới đây, công thức sai là
\[\frac{a}{{\sin A}} = 2R\,\];
\[\sin A = \frac{a}{{2R}}\,\];
\[b\sin B = 2R\,\];
\[\sin C = \frac{{c\sin A}}{a}\,\].
Cho tam giác \(ABC\) có \(\widehat B = 60^\circ ,\,\,BC = 8,\,AB = 5\). Độ dài cạnh \(AC\) bằng
7;
129;
49;
\(\sqrt {129} \).
Tam giác \(ABC\) có các cạnh \(BC = 3\sqrt 3 \), \(AC = 6\), \(AB = 3\). Độ lớn của góc \(A\) là
\(45^\circ \);
\(120^\circ \);
\(60^\circ \);
\(30^\circ \).
Chọn đáp án sai. Một tam giác giải được nếu biết
Độ dài 3 cạnh;
Độ dài 3 cạnh và 1 góc bất kỳ;
Số đo 3 góc;
Độ dài 2 cạnh và 2 góc bất kỳ.
Cho tam giác \(ABC\) có \(AB = 3,\,\,AC = 6\) và \(\widehat A = 60^\circ \). Bán kính của đường tròn ngoại tiếp tam giác là
3;
\(\sqrt 3 \);
\(3\sqrt 3 \);
\(6\).
Vectơ có điểm đầu là \(A\), điểm cuối là \(B\) được kí hiệu là
\(AB\);
\(\overrightarrow {BA} \);
\(\left| {\overrightarrow {AB} } \right|\);
\(\overrightarrow {AB} \).
Với \(A,\,B,\,C,\,D\) là bốn đỉnh của hình vuông thì vectơ \(\overrightarrow {BC} \) cùng hướng với vectơ
\(\overrightarrow {AD} \);
\(\overrightarrow {DA} \);
\(\overrightarrow {AC} \);
\(\overrightarrow {AB} \).
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là sai?
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
\(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \);
\(\overrightarrow {AC} = \overrightarrow {BD} \);
\(\overrightarrow {AB} = \overrightarrow {DC} \).
Cho ba điểm \(A,\,\,B,\,\,C\) phân biệt. Đẳng thức nào sau đây sai?
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \);
\(\overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {BC} \);
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \).
Cho hình vuông \(ABCD\)có cạnh bằng 8. Độ dài của vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) là
8;
16;
\(8\sqrt 2 \);
\(2\sqrt 8 \).
Cho tam giác \(ABC\) có điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \). Điểm \(M\) thỏa mãn bài toán khi
\(M\) là điểm thứ tư của hình bình hành \(ACBM\);
\(M\) là trung điểm của đoạn thẳng \(AB\);
\(M\) trùng \(C\);
\(M\) là trọng tâm tam giác \(ABC\).
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (\(\overrightarrow b \) khác \(\overrightarrow 0 \)) cùng phương khi và chỉ khi có một số \(k\) sao cho
\(\overrightarrow a \ne k\overrightarrow b \);
\(\overrightarrow a = k\overrightarrow b \);
\(\overrightarrow a + \overrightarrow b = k\);
\(\overrightarrow a - \overrightarrow b = k\).
Thực hiện phép toán vectơ \(\overrightarrow c - 8\overrightarrow c \) được kết quả là
\(9\overrightarrow c \);
\( - 8\overrightarrow c \);
\( - 7\overrightarrow c \);
\(\overrightarrow c \).
Đẳng thức nào sau đây mô tả đúng hình vẽ bên? 
\(\overrightarrow {AB} = 3\overrightarrow {AC} \);
\(\overrightarrow {AB} = - \frac{1}{3}\overrightarrow {AC} \);
\(\overrightarrow {BC} = \frac{3}{4}\overrightarrow {AC} \);
\(\overrightarrow {BC} = - 3\overrightarrow {AB} \).
Cho tam giác \[ABC\] có \[I,{\rm{ }}D\] lần lượt là trung điểm\[AB,{\rm{ }}CI\]. Đẳng thức nào sau đây là đúng?
\[\overrightarrow {BD} = \frac{1}{2}\overrightarrow {AB} - \frac{3}{4}\overrightarrow {AC} \];
\[\overrightarrow {BD} = - \frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \];
\[\overrightarrow {BD} = - \frac{1}{4}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \];
\[\overrightarrow {BD} = - \frac{3}{4}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \].
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Nếu vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow b \) thì góc giữa hai vectơ bằng
\(0^\circ \);
\(90^\circ \);
\(180^\circ \);
Đáp án khác.
Trong tam giác \(ABC\) có \(AB = 10,\,\,AC = 12,\,\widehat {BAC} = 120^\circ \). Khi đó, \(\overrightarrow {AB} \cdot \overrightarrow {AC} \) bằng
30;
60;
– 30;
– 60.
Cho hai vectơ \(\vec a\) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và hai vectơ \(\vec u = \frac{2}{5}\overrightarrow a - 3\overrightarrow b \) và \(\vec v = \overrightarrow a + \overrightarrow b \) vuông góc với nhau. Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b .\)
\(\alpha = 90^\circ \);
\(\alpha = 180^\circ \);
\(\alpha = 60^\circ \);
\(\alpha = 45^\circ \).
II. Tự luận (3 điểm)
(1 điểm) Một xí nghiệp có ba nhóm máy I, II, III dùng để sản xuất ra hai loại sản phẩm \(A\)và \(B\). Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
Nhóm | Số máy trong mỗi nhóm | Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm | |
Loại \(A\) | Loại \(B\) | ||
I | 15 | 3 | 3 |
II | 4 | 0 | 2 |
III | 12 | 2 | 4 |
Một đơn vị sản phẩm loại \(A\) lãi 40 nghìn đồng, một đơn vị sản phẩm loại \(B\) lãi 50 nghìn đồng. Hỏi xí nghiệp cần sản xuất bao nhiêu sản phẩm mỗi loại để có lãi cao nhất?
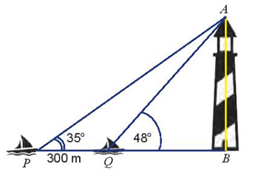
(1 điểm) Hai chiếc tàu thủy \(P\) và \[Q\] cách nhau 300 m và thẳng hàng với chân \(B\) của tháp hải đăng \(AB\) ở trên bờ biển (hình bên). Từ \(P\) và \(Q,\) người ta nhìn thấy tháp hải đăng \(AB\) dưới các góc \(\widehat {BPA} = 35^\circ \) và \(\widehat {BQA} = 48^\circ \). Tính chiều cao (làm tròn đến hàng phần trăm) của tháp hải đăng đó.
(1 điểm) Cho tứ giác \(ABCD\), hai điểm \(M,\,N\) thỏa mãn \[2\overrightarrow {MB} + \overrightarrow {MA} = \overrightarrow 0 \], \[2\overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow 0 \] và \[\frac{{AD}}{{BC}} = x\]. Tính \[\frac{{\cos \widehat {DBC}}}{{\cos \widehat {ADB}}}\] theo \(x\) để \[MN \bot BD\].