Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 3)

b) Rút gọn biểu thức \(M\).

c) Tìm giá trị nguyên của \(x\) để \(M\) nhận giá trị nguyên.

Một hãng máy bay có giá vé đi từ Thành phố Hồ Chí Minh ra Phú Yên là \[1200{\rm{ }}000\]đồng/ người. Trong đó quy định mỗi khách hàng chỉ được mang lên sân bay tối đa 7 kg hành lý. Nếu vượt quá 7 kg hành lý trở đi bắt đầu từ 7 kg trở đi cứ mỗi kg phải trả thêm \[100\,\,000\] đồng cho tiền phạt hành lý. Gọi \[y\] (đồng) là số tiền mỗi người cần trả khi đặt vé đi máy bay từ Thành phố Hồ Chí Minh ra Phú Yên, \[x{\rm{ }}\left( {{\rm{kg}}} \right)\] là khối lượng hành lý người đó mang theo.

a) Viết công thức \[y\] theo \[x\]. Cho biết \[y\] có phải là hàm số của \[x\] không? Vì sao?

b) Một người đặt vé đi máy bay từ Thành phố Hồ Chí Minh ra Phú Yên và mang theo 9 kg hành lý. Hỏi người đó phải trả tổng cộng bao nhiêu tiền?

Anh Long muốn mua một điện thoại di động iPhone 16 Pro để tặng vợ. Cửa hàng di động có chương trình khuyến mãi lớn, giảm 10% so với giá ban đầu. Do anh Long là khách hàng VIP nên được giảm thêm 5% so với giá đã giảm. Tổng số tiền giảm hai lần là \[3\,\,915\,\,000\] đồng. Hỏi giá ban đầu của điện thoại iPhone 16 Pro là bao nhiêu?

a) Tính tổng khối lượng các loại hạt điều thu hoạch được.

b) Tính xác suất thực nghiệm của các biến cố: “Hạt điều đạt loại 2 và loại 3” (làm tròn kết quả đến chữ số thập phân thứ tư).

c) Công ty lấy ngẫu nhiêm 100 kg hạt điều chưa phân loại và tiến hành phân loại. Em hãy dự đoán xem có bao nhiêu kilôgam hạt điều loại 1?

a) Chứng minh:\[A{B^2} = BH \cdot BC\].

b) Kẻ đường phân giác \[CD\]của tam giác \[ABC\]\[\left( {D \in AB} \right)\]. Tính độ dài\[DA\].

c) Từ \[B\]kẻ đường thẳng vuông góc với đường thẳng \[CD\] tại \[E\]và cắt đường thẳng \[AH\]tại \[F.\]Trên đoạn thẳng \[CD\] lấy điểm \[G\]sao cho\[BA = BG\].  Chứng minh: \[BG \bot FG\].

Một cây cao \[12\,\,{\rm{m}}\]mọc cạnh bờ sông. Trên đỉnh cây có một con chim đang đậu và chuẩn bị sà xuống bắt con cá trên mặt nước (như Hình 1 và được mô phỏng như Hình 2). Hỏi con chim sẽ bay một đoạn ngắn nhất bằng bao nhiêu mét thì bắt được con cá? (Biết con cá cách gốc cây \[5\,\,{\rm{m}}\] và nước cao mấp mé bờ sông).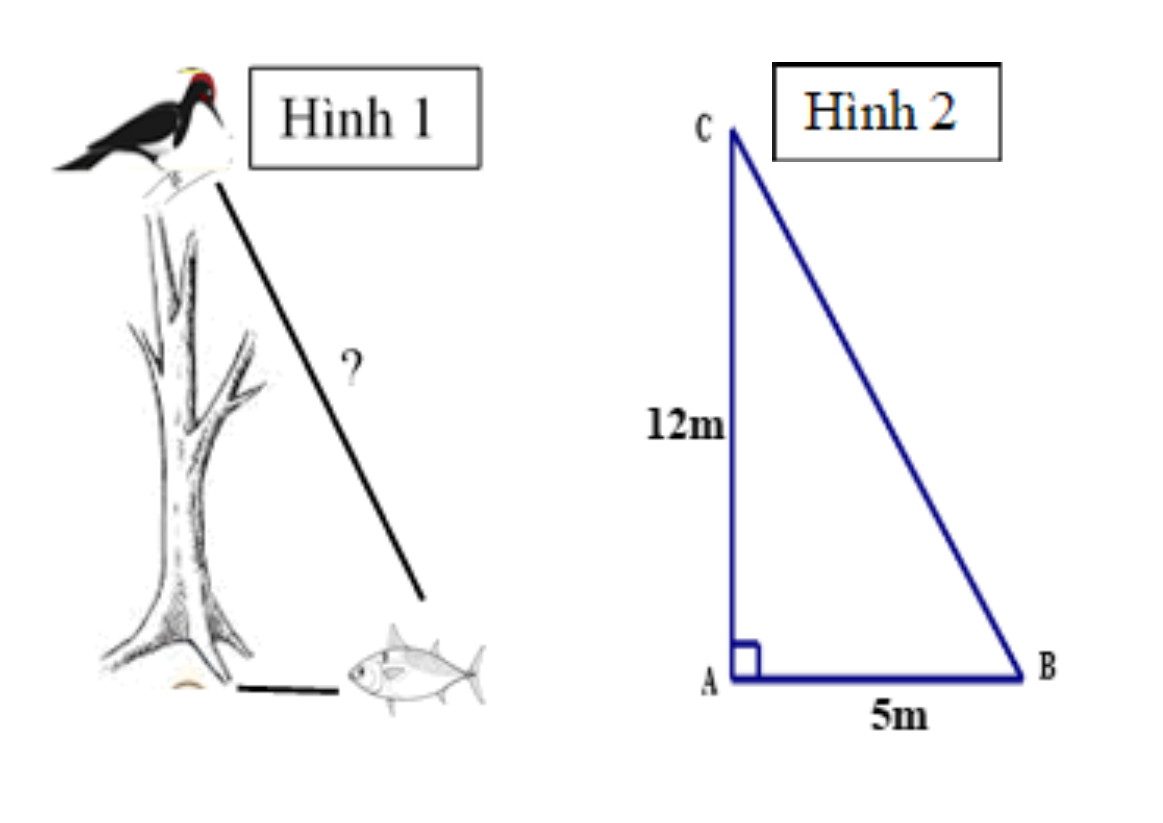

Một chiếc lều có hình dạng là một hình chóp tứ giác đều. Biết chiếc lều có mặt bên là tam giác đều có cạnh bằng \(2\,\,{\rm{m}}\). Tính chiều cao của chiếc lều.

(0,5 điểm) Cho 3 hộp đựng thẻ. Hộp 1 chứa các tấm thẻ đánh số \(\left\{ {1\,;\,\,2\,;\,\,3} \right\},\) hộp 2 chứa các thẻ đánh số \(\left\{ {2\,;\,\,4\,;\,\,6\,;\,\,8} \right\},\) hộp 3 chứa các thẻ đánh số \(\left\{ {1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9\,;\,\,11} \right\}.\) Từ mỗi hộp rút ngẫu nhiên một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.