Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 08

Phần 2. Câu trắc nghiệm đúng sai

Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Cho biểu thức  

a) Điều kiện của và để biểu thức có nghĩa là và

b) Biểu thức

c) Với thì giá trị của biểu thức là .

d) Khi thì và

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Cho bất phương trình . Tìm nghiệm nguyên nhỏ nhất của bất phương trình trên.

Cho hình vành khuyên giới hạn bởi hai đường tròn và . Hỏi diện tích hình vành khuyên đó là bao nhiêu ? (Lấy kết quả làm tròn đến hàng phần chục).

Cho hai biểu thức: và với Tính giá trị của khi .

Cho hai biểu thức: và với Rút gọn biểu thức

Cho hai biểu thức: và với Tìm giá trị của để phương trình nhận giá trị nguyên.

Giải phương trình

Giải bất phương trình

Giải bài toán bằng cách lập hệ phương trình.

Một đội công nhân và làm chung một công việc và dự định hoàn thành trong ngày. Khi làm chung được ngày thì đội được điều động đi làm việc khác, đội tăng gấp đôi năng suất, do đó đội đã hoàn thành phần việc còn lại trong ngày tiếp theo. Hỏi với năng suất ban đầu thì mỗi đội làm một mình sẽ hoàn thành công việc đó trong bao lâu?

 Một người có tầm mắt cao đứng trên sân thượng của một tòa nhà cao nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống (như hình vẽ).Viết tỉ số lượng giác của góc theo các cạnh

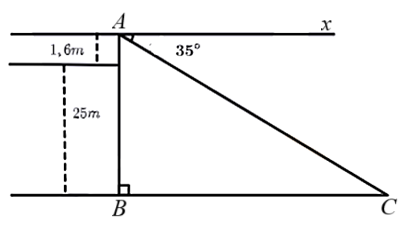
Một người có tầm mắt cao đứng trên sân thượng của một tòa nhà cao nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống (như hình vẽ).Tính các khoảng cách từ chiếc xe đến mắt người quan sát và đến chân tòa nhà (kết quả làm tròn đến hàng đơn vị).

Cho đường tròn và một điểm nằm ngoài đường tròn. Từ kẻ hai tiếp tuyến ( là các tiếp điểm). Từ kẻ đường thẳng cắt đường tròn tại hai điểm và (điểm nằm giữa và Gọi là trung điểm của dây , là giao điểm thứ hai của đường thẳng với đường tròn .Chứng minh bốn điểm cùng thuộc một đường tròn.

 Cho đường tròn và một điểm nằm ngoài đường tròn. Từ kẻ hai tiếp tuyến ( là các tiếp điểm). Từ kẻ đường thẳng cắt đường tròn tại hai điểm và (điểm nằm giữa và Gọi là trung điểm của dây , là giao điểm thứ hai của đường thẳng với đường tròn .Chứng minh và .

 Cho đường tròn và một điểm nằm ngoài đường tròn. Từ kẻ hai tiếp tuyến ( là các tiếp điểm). Từ kẻ đường thẳng cắt đường tròn tại hai điểm và (điểm nằm giữa và Gọi là trung điểm của dây , là giao điểm thứ hai của đường thẳng với đường tròn .Xác định vị trí của để diện tích tam giác lớn nhất.

Xưa kia có một vị tể tướng nổi tiếng thông thái. Đến khi tể tướng muốn cáo quan về quê, nhà vua liền ban thưởng bằng cách đưa cho tể tướng một đoạn dây dài mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Khi đó, mảnh đất hình chữ nhật sẽ thuộc về ngươi”. Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?