Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 07
18 câu hỏi
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
Cho 
. Khi đó, ta có
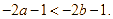
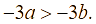
Cho tam giác 
vuông tại 
. Hệ thức nào dưới đây là đúng?
Hình vành khuyên giới hạn bởi hai đường tròn 
và 
có diện tích bằng
Cho biểu thức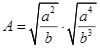 
.
a) Điều kiện xác định của biểu thức 
là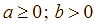 
.
b) Rút gọn biểu thức ta được 
c) Giá trị của tại 
và 
là 
d) Giá trị của 
khi 
và 
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Cho bất phương trình 
. Tìm nghiệm âm lớn nhất của bất phương trình đó.
Cung tròn 
của một đường tròn có độ dài là 
Tính bán kính của đường tròn đó.
Cho hai biểu thức: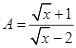 
và 
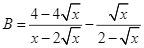với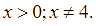 
Tính giá trị biểu thức 
khi 
Cho hai biểu thức: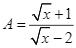 
và 
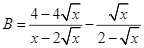với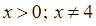 
Chứng minh rằng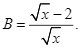 
Cho hai biểu thức: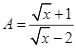 
và 
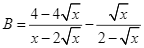với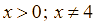 
Xét biểu thức 
. Tìm tất cả các giá trị nguyên của 
để 
nguyên.
Giải phương trình 
Giải bất phương trình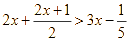
Giải bài toán sau bằng cách lập hệ phương trình.
Hai vòi nước cùng chảy vào một bể không có nước thì sau 1 giờ 20 phút sẽ đầy. Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ hai chảy trong 12 phút thì đầy 
bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu mới đầy bể?
Trong một lần đến tham quan tháp Eiffel (Paris, Pháp), bạn Vân muốn ước tính độ cao của tháp. Sau khi quan sát, bạn Vân đã minh họa lại kết quả đo đạc như hình dưới đây. Em hãy giúp bạn Vân tính độ cao 
của tháp Eiffel theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Cho đường tròn 
và một điểm 
nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ tiếp xúc với đường tròn tại 
và 
. Gọi 
là giao điểm của 
và 
, kẻ đường kính 
của đường tròn , hạ 
tại 
Tia 
cắt đường tròn tại 
.Chứng minh rằng 
.
Cho đường tròn 
và một điểm 
nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ tiếp xúc với đường tròn tại 
và 
. Gọi 
là giao điểm của 
và 
, kẻ đường kính 
của đường tròn , hạ 
tại 
Tia 
cắt đường tròn tại 
.Chứng minh rằng 
là phân giác của 
Cho đường tròn 
và một điểm 
nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ tiếp xúc với đường tròn tại 
và 
. Gọi 
là giao điểm của 
và 
, kẻ đường kính 
của đường tròn , hạ 
tại 
Tia 
cắt đường tròn tại 
.Cho 
và 
. Tính diện tích hình quạt giới hạn bởi các bán kính 
và cung nhỏ 
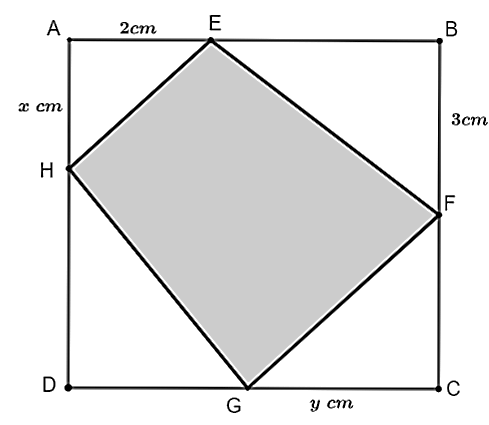
Cho một mảnh giấy hình vuông 
cạnh 
. Gọi 
lần lượt là hai điểm nằm trên cạnh 
và 
sao cho 
; 
. Bạn Nam muốn cắt một hình thang 
(như hình bên) sao cho hình thang đó có diện tích nhỏ nhất. Xác định vị trí của 
trên cạnh để bạn Nam có thể thực hiện mong muốn của mình?
