Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 05
23 câu hỏi
Điều kiện xác định của phương trình 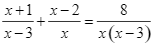 là
là
![]()
![]()
![]()
![]()
Hệ phương trình 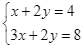 có nghiệm là
có nghiệm là
![]()
![]()
![]()
![]()
Bất đẳng thức ![]() có thể được phát biểu là
có thể được phát biểu là
lớn hơn ![]()
nhỏ hơn ![]()
không lớn hơn ![]()
không nhỏ hơn ![]()
Nghiệm của bất phương trình ![]() là
là
![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Điều kiện xác định của biểu thức ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?
![]()
![]()
![]()
![]()
Giá trị của biểu thức ![]() là
là
![]()
![]()
![]()
![]()
Giá trị ![]() (kết quả làm tròn đến chữ số thập phân thứ ba) là
(kết quả làm tròn đến chữ số thập phân thứ ba) là
![]()
![]()
![]()
![]()
Cho tam giác ![]() vuông tại
vuông tại ![]() có
có ![]() Độ dài hai cạnh còn lại là
Độ dài hai cạnh còn lại là
![]()
![]()
![]()
![]()
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn
Cắt nhau.
Tiếp xúc nhau.
Ngoài nhau.
Không xác định.
Độ dài cung ![]() của một đường tròn có bán kính
của một đường tròn có bán kính ![]() là
là
![]()
![]()
![]()
![]()
Cho đường tròn ![]() , dây
, dây ![]() vuông góc với bán kính
vuông góc với bán kính ![]() tại trung điểm
tại trung điểm ![]() của
của ![]() . Dây
. Dây ![]() có độ dài là
có độ dài là
![]()
![]()
![]()
![]()
Cho hai biểu thức: ![]() và
và 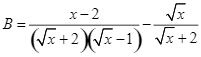 với
với ![]() Tính giá trị của biểu thức
Tính giá trị của biểu thức ![]() khi
khi ![]()
Cho hai biểu thức: ![]() và
và 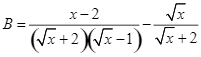 với
với ![]() Rút gọn biểu thức
Rút gọn biểu thức ![]()
Cho hai biểu thức: ![]() và
và 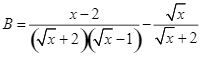 với
với ![]() Tìm các giá trị
Tìm các giá trị ![]() để
để ![]() có nghiệm
có nghiệm ![]()
Giải phương trình![]()
Giải bất phương trình ![]()
Giải bài toán sau bằng cách lập hệ phương trình.
Một chiếc xe khách đi từ Thành phố Hồ Chí Minh đến Cần Thơ, quãng đường dài ![]() km. Sau khi xe khách xuất phát 1 giờ 40 phút, một xe tải bắt đầu đi từ Cần Thơ về Thành phố Hồ Chí Minh và gặp xe khách sau đó 40 phút. Tính vận tốc của mỗi xe, biết rằng mỗi giờ xe khách đi nhanh hơn xe tải là
km. Sau khi xe khách xuất phát 1 giờ 40 phút, một xe tải bắt đầu đi từ Cần Thơ về Thành phố Hồ Chí Minh và gặp xe khách sau đó 40 phút. Tính vận tốc của mỗi xe, biết rằng mỗi giờ xe khách đi nhanh hơn xe tải là ![]() km.
km.
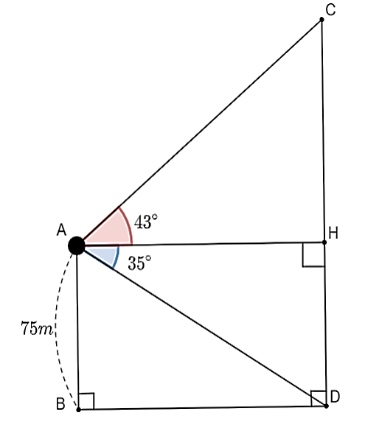
Một kĩ sư xây dựng đứng ở vị trí ![]() (nóc của tòa nhà) dùng thiết bị để quan sát trạm thu phát sóng. Kĩ sư quan sát đỉnh
(nóc của tòa nhà) dùng thiết bị để quan sát trạm thu phát sóng. Kĩ sư quan sát đỉnh ![]() và chân
và chân ![]() của trạm thu phát sóng dưới hai góc nhìn (so với phương ngang) lần lượt là
của trạm thu phát sóng dưới hai góc nhìn (so với phương ngang) lần lượt là ![]() và
và ![]() . Biết chiều cao của tòa nhà là
. Biết chiều cao của tòa nhà là ![]() , hãy tính chiều cao
, hãy tính chiều cao ![]() của trạm phát sóng (kết quả làm tròn đến hàng phần trăm).
của trạm phát sóng (kết quả làm tròn đến hàng phần trăm).
Cho hai tiếp tuyến ![]() và
và ![]() của đường tròn tâm
của đường tròn tâm ![]() (
(![]() là hai tiếp điểm). Vẽ đường kính
là hai tiếp điểm). Vẽ đường kính ![]() ,
, ![]() cắt
cắt ![]() tại
tại ![]() . Chứng minh bốn điểm
. Chứng minh bốn điểm ![]() cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
Cho hai tiếp tuyến ![]() và
và ![]() của đường tròn tâm
của đường tròn tâm ![]() (
(![]() là hai tiếp điểm). Vẽ đường kính
là hai tiếp điểm). Vẽ đường kính ![]() ,
, ![]() cắt
cắt ![]() tại
tại ![]() . Chứng minh
. Chứng minh ![]() vuông góc với
vuông góc với ![]() và
và ![]() .
.
Cho hai tiếp tuyến ![]() và
và ![]() của đường tròn tâm
của đường tròn tâm ![]() (
(![]() là hai tiếp điểm). Vẽ đường kính
là hai tiếp điểm). Vẽ đường kính ![]() ,
, ![]() cắt
cắt ![]() tại
tại ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() và
và ![]() cắt
cắt ![]() tại
tại ![]() . Chứng minh
. Chứng minh ![]() thẳng hàng.
thẳng hàng.
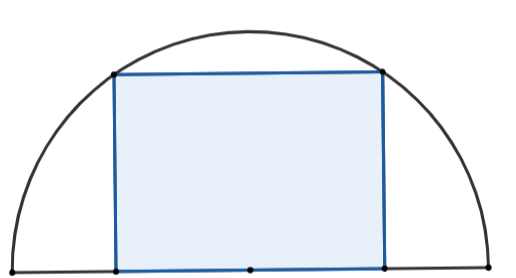
Một khu đất có dạng nửa hình tròn với bán kính là ![]() Người ta muốn xây dựng một khu vui chơi hình chữ nhật nội tiếp nửa đường tròn (như hình vẽ). Biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.
Người ta muốn xây dựng một khu vui chơi hình chữ nhật nội tiếp nửa đường tròn (như hình vẽ). Biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.