Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 01
20 câu hỏi
Điều kiện xác định của phương trình 
là
Đâu là một hệ phương trình bậc nhất hai ẩn?
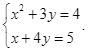
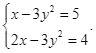
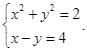
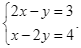
Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn?
Điều kiện xác định của 
là
Rút gọn biểu thức 
với 
ta có kết quả
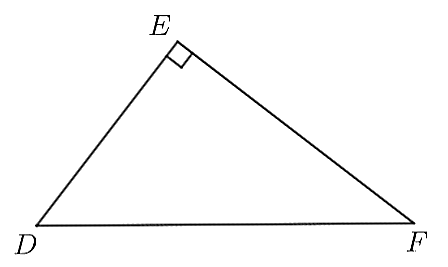
Cho tam giác 
vuông tại 
. Hệ thức nào dưới đây là đúng?
Đường thẳng 
cách tâm 
của đường tròn 
một khoảng 
Khi đó vị trí tương đối của và đường tròn là
Cắt nhau.
Không giao nhau.
Tiếp xúc nhau.
Không kết luận được.
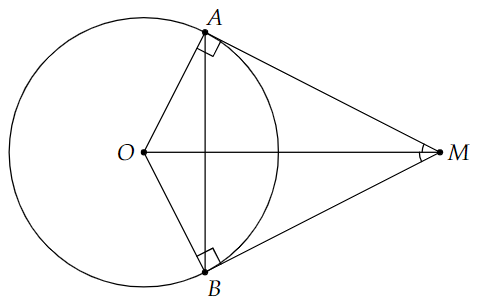
Cho tiếp tuyến của đường tròn 
tại 
và 
cắt nhau tại 
. Biết 
Số đo cung nhỏ 
là
B. TỰ LUẬN (8,0 điểm)
Cho hai biểu thức 
và 
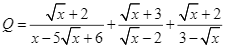với
Tính giá trị của 
tại 
Cho hai biểu thức 
và 
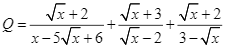với
Rút gọn biểu thức 
.
Cho hai biểu thức 
và 
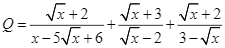với
Biết 
. Tìm số nguyên 
để 
Giải các phương trình, bất phương trình sau:
Giải các phương trình, bất phương trình sau:
Giải bài toán sau bằng cách lập hệ phương trình.
Người ta trộn hai loại quặng sắt với nhau, loại I chứa 72% sắt, loại II chứa 58% sắt được một loại quặng chứa 62% sắt. Nếu tăng khối lượng của mỗi loại quặng thêm 15 tấn thì được một loại quặng mới chứa 
sắt. Tìm khối lượng ban đầu của mỗi loại quặng đã trộn.
Tháp chung cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 
và bóng của tòa nhà trên mặt đất dài khoảng 
.Tính chiều cao của tòa tháp chung cư (làm tròn đến kết quả hàng đơn vị).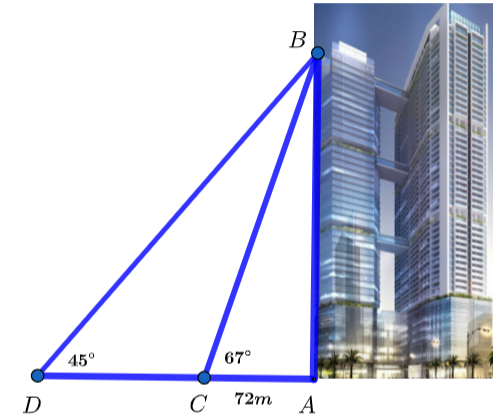
Tháp chung cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 
và bóng của tòa nhà trên mặt đất dài khoảng 
.Một flycam từ vị trí 
bay lên đỉnh 
theo quãng đường 
, tạo với phương nằm ngang một góc bằng 
. Biết flycam mất 
giây để lên đến đỉnh tòa tháp. Tính vận tốc trung bình của chiếc flycam đó (làm tròn kết quả đến hàng phần trăm).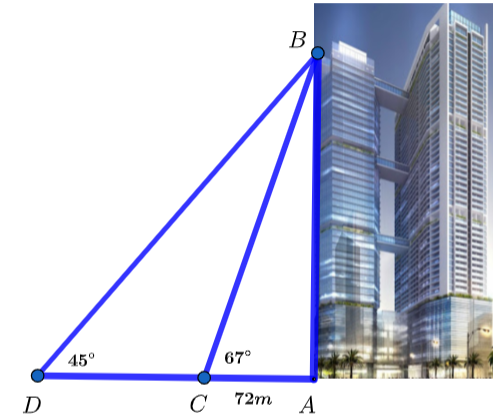
Cho đường tròn 
đường kính 
. Lấy điểm 
thuộc sao cho 
Vẽ dây 
vuông góc với tại 
. Đường thẳng 
cắt 
tại 
. Đường thẳng qua vuông góc với tại 
và cắt 
tại 
.Chứng minh 
cùng thuộc một đường tròn.
ho đường tròn 
đường kính 
. Lấy điểm 
thuộc sao cho 
Vẽ dây 
vuông góc với tại 
. Đường thẳng 
cắt 
tại 
. Đường thẳng qua vuông góc với tại 
và cắt 
tại 
.Chứng minh 
là tia phân giác của 
.
Cho đường tròn 
đường kính 
. Lấy điểm 
thuộc sao cho 
Vẽ dây 
vuông góc với tại 
. Đường thẳng 
cắt 
tại 
. Đường thẳng qua vuông góc với tại 
và cắt 
tại 
.Chứng minh 
cân và 
là tiếp tuyến của đường tròn 
.
Một sợi dây thép 
có chiều dài 
được chia thành hai phần 
(như hình vẽ minh họa dưới đây).
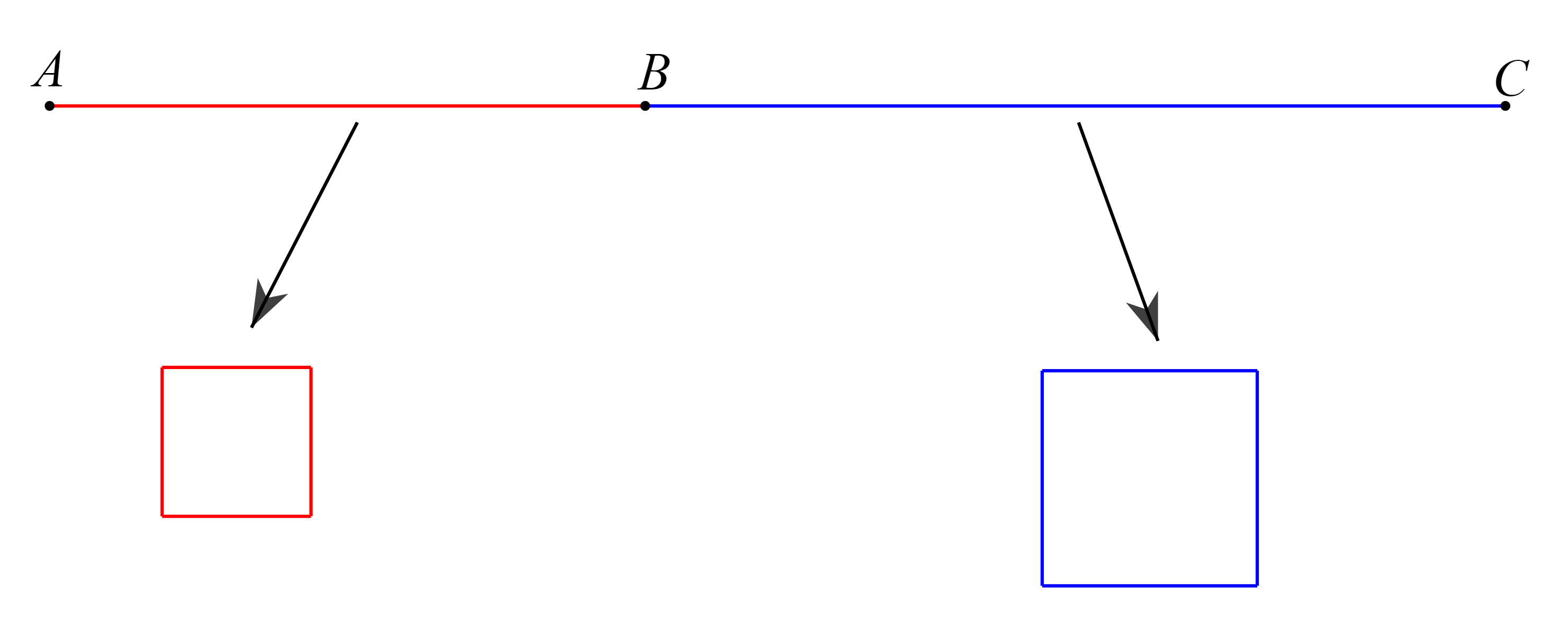
Mỗi phần đều được uốn thành một hình vuông. Hỏi phải chia sợi dây ban đầu như thế nào để tổng diện tích hai hình vuông thu được sau khi uốn là nhỏ nhất?
