Bộ 10 đề thi cuối kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 05
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() có bảng xét dấu của đạo hàm như sau
có bảng xét dấu của đạo hàm như sau
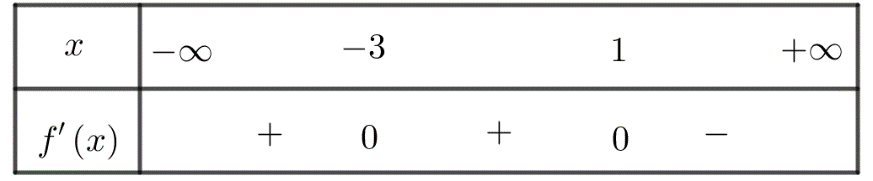
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() có
có ![]() ,
, ![]() .
.
Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng ![]() .
.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho không có tiệm cận ngang
Gọi giá trị nhỏ nhất và giá trị lớn nhất của hàm số ![]() trên nửa khoảng
trên nửa khoảng ![]() lần lượt là
lần lượt là ![]() và
và ![]() . Giá trị của biểu thức
. Giá trị của biểu thức ![]() bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
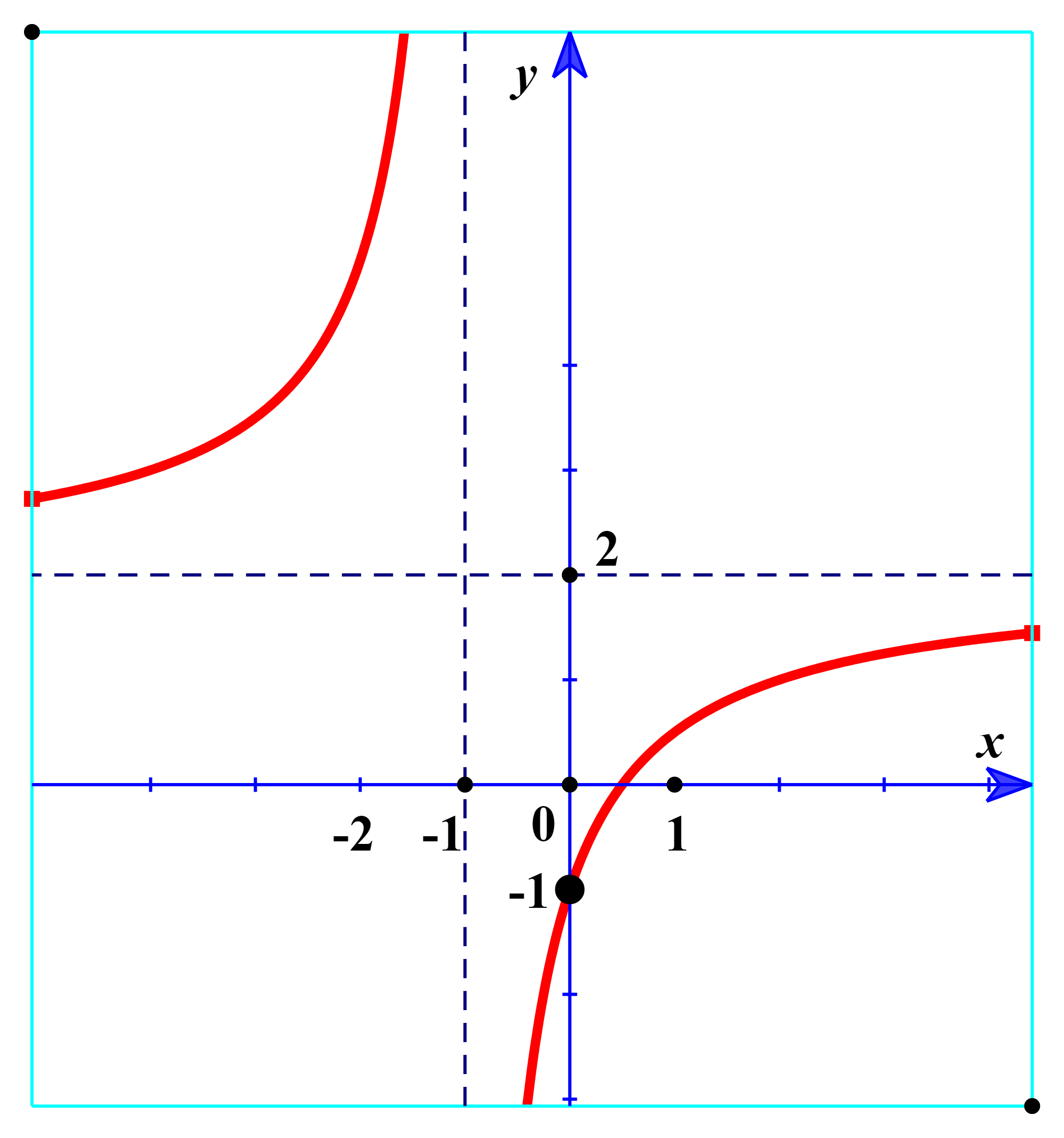
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình hộp ![]()
![]() . Vectơ nào dưới đây cùng phương với vectơ
. Vectơ nào dưới đây cùng phương với vectơ ![]()
![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Tọa độ của vectơ
. Tọa độ của vectơ ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ trục tọa độ ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Tọa độ của vectơ
. Tọa độ của vectơ ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình lăng trụ ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() . Đặt
. Đặt ![]() ,
, ![]() ,
, ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. ![]() .
.
B.![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho điểm
, cho điểm ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() , biết
, biết ![]() . Tìm tọa độ của điểm
. Tìm tọa độ của điểm ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ toạ độ ![]() , cho vectơ
, cho vectơ ![]() . Có bao nhiêu giá trị thực của
. Có bao nhiêu giá trị thực của ![]() để góc giữa vectơ
để góc giữa vectơ ![]() và vectơ
và vectơ ![]() bằng
bằng ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:
Mức giá (triệu đồng/ | [10;14) | [14;18) | [18;22) | [22;26) | [26;30) |
Số khách hàng | 54 | 78 | 120 | 45 | 12 |
Khoảng biến thiên ![]() của mẫu số liệu ghép nhóm trên là.
của mẫu số liệu ghép nhóm trên là.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Độ lệch chuẩn bằng
bình phương của phương sai.
một nửa của phương sai.
căn bậc hai số học của phương sai.
nghịch đảo của phương sai.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ
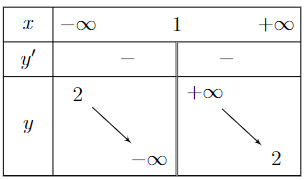 a) Hàm số đã cho nghịch biến trên
a) Hàm số đã cho nghịch biến trên ![]() .
.
b) Giá trị nhỏ nhất của hàm số là 2.
c) Tâm đối xứng của đồ thị hàm số là ![]() .
.
d) Có 2024 số nguyên ![]() trên
trên ![]() để phương trình
để phương trình ![]() có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Cho hàm số ![]() , (tham số
, (tham số ![]() ). Xét tính đúng sai của các khẳng định sau
). Xét tính đúng sai của các khẳng định sau
a) Khi ![]() thì hàm số đạt cực tiểu tại
thì hàm số đạt cực tiểu tại ![]() .
.
b) Khi ![]() thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng ![]() .
.
c) Khi ![]() thì hàm số có giá trị nhỏ nhất trên khoảng
thì hàm số có giá trị nhỏ nhất trên khoảng ![]() bằng
bằng ![]() .
.
d) Có tất cả 1 giá trị nguyên của ![]() để hàm số có giá trị nhỏ nhất trên khoảng
để hàm số có giá trị nhỏ nhất trên khoảng ![]() .
.
Trong không gian ![]() , cho
, cho ![]() , biết
, biết ![]() .
.
a) ![]() .
.
b) ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() .
.
c) ![]() thỏa mãn
thỏa mãn ![]() . Khi đó
. Khi đó ![]() .
.
d) ![]() sao cho
sao cho ![]() vuông góc với đường thẳng
vuông góc với đường thẳng ![]() . Khi đó
. Khi đó ![]()
Bác tài xế A và bác tài xế B thống kê lại độ dài quãng đường (đơn vị: km) mà hai bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Độ dài quãng đường (km) |
|
|
|
|
|
Số ngày bác tài A lái xe | 5 | 10 | 9 | 4 | 2 |
Số ngày bác tài B lái xe | 4 | 8 | 12 | 6 | 0 |
a) Khoảng biến thiên về độ dài quãng đường đi mỗi ngày của bác tài A và B ở mẫu số liệu trên bằng nhau.
b) Tứ phân vị thứ nhất của mẫu số liệu về độ dài quãng đường mỗi ngày của bác tài A lớn hơn bác tài B
c) Tứ phân vị thứ ba của mẫu số liệu về quãng đường mỗi ngày của bác tài B thuộc nhóm ![]() .
.
d) Theo khoảng biến thiên thì độ dài quãng đường mỗi ngày của bác tài A phân tán hơn độ dài quãng đường mỗi ngày bác tài B.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Cho hàm số ![]() . Tìm số đường tiệm cận xiên của đồ thị hàm số.
. Tìm số đường tiệm cận xiên của đồ thị hàm số.
Một chất điểm chuyển động theo quy luật ![]() . Vận tốc
. Vận tốc ![]() của chuyển động đạt giá trị lớn nhất tại thời điểm
của chuyển động đạt giá trị lớn nhất tại thời điểm ![]() bằng bao nhiêu giây?
bằng bao nhiêu giây?
Giả sử chi phí tiền xăng ![]() (đồng) phụ thuộc tốc độ trung bình
(đồng) phụ thuộc tốc độ trung bình ![]() theo công thức:
theo công thức: 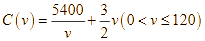 . Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
. Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
Trong không gian ![]() , cho ba điểm
, cho ba điểm ![]() ,
,![]() và
và ![]() . Điểm
. Điểm ![]() là điểm thỏa mãn
là điểm thỏa mãn ![]() đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất của
đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất của ![]() .
.
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát ![]() về phía nam và
về phía nam và ![]() về phía đông, đồng thời cách mặt đất
về phía đông, đồng thời cách mặt đất ![]() . Chiếc thứ hai nằm cách điểm xuất phát
. Chiếc thứ hai nằm cách điểm xuất phát ![]() về phía bắc và
về phía bắc và ![]() về phía tây, đồng thời cách mặt đất
về phía tây, đồng thời cách mặt đất ![]() . Người ta cần tìm một vị trí trên mặt đất để tiếp nhiên liệu cho hai khinh khí cầu sao cho tổng khoảng cách từ vị trí đó tới hai khinh khí cầu nhỏ nhất. Giả sử vị trí cần tìm cách địa điểm hai khinh khí cầu bay lên là
. Người ta cần tìm một vị trí trên mặt đất để tiếp nhiên liệu cho hai khinh khí cầu sao cho tổng khoảng cách từ vị trí đó tới hai khinh khí cầu nhỏ nhất. Giả sử vị trí cần tìm cách địa điểm hai khinh khí cầu bay lên là ![]() theo hướng nam và
theo hướng nam và ![]() theo hướng tây. Tính tổng
theo hướng tây. Tính tổng ![]() .
.
Thời gian chạy tập luyện cự li ![]() của một vận động viên được cho trong bảng sau:
của một vận động viên được cho trong bảng sau:
Thời gian ( giây) |
|
|
|
|
|
Số lần chạy | 3 | 8 | 6 | 2 | 1 |
Tính phương sai của mẫu số liệu ghép nhóm trên.








