7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 97)

Tìm các số tự nhiên tròn chục có ba chữ số lớn hơn 100 và nhỏ hơn 450.

Cho dãy số 1,2,3..........,60,61.Hỏi trong dãy số đó có bao nhiêu số lẻ?

Tính tổng 2² + 4² + 6² + ... + 20².

Cho tam giác ABC, có M là trung điểm BC. Biết A(2;2), B(0;3), C(4;-3). H là chân đường vuông góc hạ từ A xuống BC. Tính độ dài $\overrightarrow{AM},\overrightarrow{AH}$.

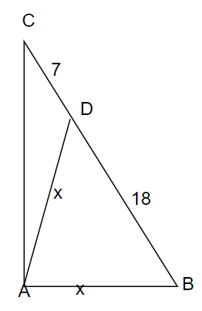
Tính độ dài x trên hình vẽ biết rằng CD = 7cm, DB = 18cm, $\widehat{BAC}=90°$.

Cho tam giác ABC vuông tại A có AB = 12cm, BC = 15cm. Tính độ dài đường cao AH và đường phân giác AD.

Tính giá trị của biểu thức A = cos 10° + cos 20° + ... + cos 170° + cos 180°.

Tính hợp lý giá trị biểu thức $B=\frac{5}{2.1}+\frac{4}{1.11}+\frac{3}{11.2}+\frac{1}{2.15}+\frac{13}{15.4}$.

Tính nhanh: 16 – 18 + 20 – 22 + 24 – 26 + … + 64 – 66 + 68.

Tính theo cách hợp lý: (3737.50 – 5050.36) : (1 + 2 + 3 + 4 + … + 100).

Tìm giá trị nguyên của x để phân số $\frac{1}{x-3}$ có giá trị nhỏ nhất.

Tìm x thuộc N, biết: x²⁰¹⁵ = x²⁰¹⁶.

Tìm x thuộc N, biết: 10 + 2x = 4⁵ : 4³.

Tìm số tự nhiên n nhỏ nhất sao cho n chia 15 dư 9 và n chia 35 dư 29.

Tính nhanh: 100 - 96 + 92 - 88 + 84 - 80 ... 12 - 8 + 4.

Tìm x biết: 15(x + 1) + 35 = 2.100².

Tính A = 1 . 3 . 5 + 3 . 5 . 7 + ... + 95 . 97 . 99.

Tính bằng cách hợp lý: 1 – 2 + 3 – 4 + … - 98 + 99.

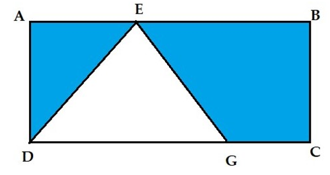
Tính diện tích của phần được tô màu dưới đây biết: độ dài cạnh AB = 12 cm, BC = 4 cm và DG = 9 cm.

Tìm số tự nhiên x biết:

a) $\frac{x}{100}=\frac{3}{25}$;

b) $\frac{x}{5}<\frac{4}{10}$.

Tìm số tự nhiên nhỏ nhất sao cho chia 11 dư 6, chia 4 dư 1, chia 19 dư 11.

Tìm số tự nhiên x, y để $\overline{234xy}$ chia hết cho 2; 5; 9.

Tìm số tự nhiên có 2 chữ số giống nhau biết rằng số đó chia hết cho 2 và chia cho 5 thì dư 3.

Tìm tập giá trị của hàm số y = cos5x – sin5x.

Tìm tập xác định của hàm số $\sqrt{3-2\cos x}$.

Tìm tất cả các số nguyên dương n sao cho tất cả các số n + 1, n + 5, n + 7, n + 13, n + 17, n + 25, n + 37 đều là số nguyên tố.

Tìm tất cả các số tự nhiên n (1 ≤ n ≤ 2000) để biểu thức B = 1.3 + 2.4 +...+ n(n + 2) chia hết cho 2027.

Tìm tổng 4 số nguyên dương phân biệt mà tổng 3 số bất kì trong chúng là một số nguyên tố.

Cho $A=\left(\frac{3x+1}{3x-1}-\frac{3x-1}{3x+1}\right):\frac{3x}{6x-2}$.

a) Rút gọn A.

b) Tìm x để A > 0.

Cho biểu thức $P=\frac{1}{\sqrt{x}-2}-\frac{4}{x-4}$.

a) Tìm ĐKXĐ của P.

b) Rút gọn P.

c) Tìm x để $P\ge \frac{1}{5}$.

Tìm tổng nghiệm dương bé nhất và nghiệm âm lớn nhất của phương trình sinx = cos2x.

Tìm một số có 3 chữ số, biết rằng chữ số hàng trăm gấp 2 lần chữ số hàng chục, chữ số hàng chục gấp 3 lần chữ số hàng đơn vị.

Tìm số tự nhiên n > 1, sao cho:

a) n + 5 chia hết cho n + 1;

b) 2n + 1 chia hết cho n – 1.

Tìm phân số $\frac{a}{b}$ thỏa mãn điều kiện: $\frac{4}{7}<\frac{a}{b}<\frac{2}{3}$ và 7a + 4b = 1994.

Tìm số nguyên tố p để p + 2 và p + 10 cũng là số nguyên tố.

Tìm số có 2 chữ số biết số đó chia hết cho tích 2 chữ số của nó.

Số 20! có tận cùng là bao nhiêu chữ số 0?

Tìm số hạng thứ 10 của dãy số sau: 1; 5; 9; 13; ...

Số nghiệm trên đoạn [0;2π] của phương trình sin2x −2cosx = 0 là bao nhiêu?

Tìm số nguyên tố p sao cho: 5p + 3 là số nguyên tố.

Tìm số nguyên tố p, sao cho p + 2, p + 4 cũng là các số nguyên tố.

Tìm số tự nhiên có hai chữ số, các chữ số giống nhau, biết rằng số đó chia hết cho 2, còn chia cho 5 dư 4.

Tìm một số tự nhiên có 6 chữ số, biết rằng chữ số hàng đơn vị là 4 và nếu chuyển chữ số đó lên hàng đầu tiên thì số đó tăng gấp 4 lần.

Tìm tất cả các số tự nhiên n thỏa mãn 5n + 14 chia hết cho n + 2.

Tìm số tự nhiên nhỏ nhất biết số đó chia 12 dư 2 và chia 10 dư 2.

Tìm m để đường thẳng d: y = mx + 1 cắt đường thẳng d′: y = 2x – 1 tại 1 điểm thuộc đường phân giác góc phần tư thứ II và thứ IV.

Cho A = [1 ; 5] , B = [2m - 1 ; m + 2) , tìm m để:

a) A ∩ B = ∅.

b) A giao B chỉ có đúng 1 phần tử.

Tìm m để (d₁); (d₂); (d₃) đồng quy:

(d₁):y = 2x + 1

(d₂): y = (m - 1)x + m

(d₃): y = 3x - 1

Cho 2 đường thẳng y = x - 2m + 1 (d₁) và y = 2x - 3 (d₂). Tìm m để 2 đường thẳng d₁ cắt d₂ tại 1 điểm nằm trên trục tung.

Cho (d₁): y = (2m + 1)x – 2m – 3 và (d₂): y = (m – 1)x + m. Tìm m để (d₁) và (d₂) cắt nhau tại 1 điểm nằm trên trục hoành.

Cho hàm số y = (m – 2)x + m + 1 (d). Tìm m để (d) đi qua gốc tọa độ.

Cho đường thẳng y = (1 - 4m)x + m – 2.

Với giá trị nào của m thì đường thẳng tạo với trục Ox 1 góc nhọn, góc tù?

Tìm m để đường thẳng y = m(x + 1) − 2 cắt đồ thị hàm số y = x³ + 3x² − 4 tại ba điểm phân biệt.

Tìm m để hàm số y = x³ − 6x² + mx + 1 đồng biến trên (0; +∞).

A. m ≥ 12

B. m ≤ 12

C. m ≥ 0

D. m ≤ 0

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 

x⁴ − 4x² – 4 + 2m = 0 có 4 nghiệm phân biệt.

Khi xóa đi chữ số hàng trăm của 1 số có 3 chữ số thì số đó giảm đi 7 lần. Tìm số có 3 chữ số đó.

Tìm m để đồ thị hàm số $y=\frac{\left(1-m\right)x-1}{2x+m}$ có đường tiệm cận ngang đi qua điểm A(2; -1).

Tìm các chữ số a và b biết rằng:

a) $\overline{25a2b}$⋮ 36

b) $\overline{a378b}$ ⋮ 72

Tìm số tự nhiên x,y biết $\overline{5x2y}$ chia hết cho 2, cho 5 và chia hết cho 9.

Tìm các số tự nhiên a và số nguyên tố p để a³ = 2p + 1.

Tìm chu kỳ của hàm số $f\left(x\right)=\sin \frac{x}{2}+2\cos \frac{3x}{2}$.

Tìm điểm cực trị của hàm số y = 2sinx - cos2x.

Tính trung bình cộng của dãy số sau: 2 + 6 + 10 + 14 + ... + 102 + 106.

Tìm GTLN của biểu thức $C=\frac{x+2}{\left|x\right|}$.

Tìm GTNN, GTLN của hàm số $y=\frac{2\sin x-1}{\sin x+2}$.

Tìm GTNN của biểu thức $\text{}B=\sqrt{x-5}+\sqrt{7-x}$.

Tìm GTNN của biểu thức $P=\frac{3x+6\sqrt{x}+27}{\sqrt{x}+2}$.

Tìm 2 số tự nhiên lớn hơn 0 sao cho tích hai số đó gấp đôi tổng của chúng.

Tìm GTNN của biểu thức P = x² + y² biết x + 2y = 3.

Tìm 2 số tự nhiên nhỏ nhất a và b thỏa mãn ƯCLN(a, b) = 12 và a – b = 84.

Tìm 3 số hạng của một cấp số nhân mà tổng là 19 và tích là 216.

Tìm a, b sao cho $\overline{aabb}$ là số chính phương.

Nêu lý thuyết về đại lượng tỉ lệ thuận, tỉ lệ nghịch lớp 5.

Tích các số 2.4.6.8.10 có mấy chữ số 0 tận cùng?

Tích các số 1.2.3.4.5….49.50 có bao nhiêu chữ số 0?

Công thức tính tích của một dãy số cách đều.

Công thức tính tích của một dãy số cách đều.

Cho biểu thức $A=\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{\sqrt{x}-1}{\sqrt{x}+1}+\frac{3\sqrt{x}+1}{1-x}$.

a) Rút gọn A.

b) Tính A khi $x=\frac{1}{\sqrt{2}}$.

Tập hợp A các số tự nhiên lẻ nhỏ hơn 294. Hỏi tập hợp A có bao nhiêu phần tử?

Tập hợp tất cả các giá trị thực của m để hàm số $y=\frac{x+4}{x+m}$ đồng biến trên khoảng (–∞; –7) là:

A. [4; 7).            

B. (4; 7).                

C. (4; 7].     

D. (4; +∞).

Tìm tập xác định của hàm số y = cos2x.

Tập hợp các chữ cái trong cụm từ “THÁI BÌNH" là:

A. {THAI; BINH}.

B. {T; H; A; I; B; N}.

C. {T; H; A; I; B; N; H}.

D. {T; H; A; I; B; I; N; H}.

Tập hợp các chữ cái trong cụm từ “THÁI BÌNH" là:

A. {THAI; BINH}.

B. {T; H; A; I; B; N}.

C. {T; H; A; I; B; N; H}.

D. {T; H; A; I; B; I; N; H}.

Tại cửa hàng giá niêm yết một cái áo là 300000 đồng. Nếu bán với giá bằng ba phần tư giá niêm yết thì được lãi 20%. Hỏi để lãi 40% thì cửa hàng bán giá niêm yết là bao nhiêu?

Rút gọn $\frac{\sqrt{8-\sqrt{15}}}{\sqrt{30}-\sqrt{2}}$.

Giải phương trình $2\sqrt{9x-18}-\sqrt{25x-50}+\sqrt{x-2}=6$.

Rút gọn biểu thức $\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}$ với x ≥ 2.

Sử dụng 3 chữ số khác nhau từ các chữ số 0, 1, 2, 4, 5, 7, 8 để tạo thành các số lẻ có 3 chữ số. Hỏi có thể tạo ra được bao nhiêu số khác nhau?

Số học sinh khối 6 của trường Kết Đoàn khoảng từ 300 đến 400 học sinh. Mỗi lần xếp hàng 12, hàng 15, hàng 18 đều vừa đủ. Hỏi khối 6 của trường Kết Đoàn có bao nhiêu học sinh?

Tìm số lớn nhất có 5 chữ số mà tổng các chữ số bằng 9.

Số nào sau đây được viết dưới dạng số thập phân hữu hạn?

A. $\frac{7}{18}$.

B. $\frac{3}{20}$.

C. $\frac{11}{75}$.

D. $\frac{-73}{99}$.

Tại "Ngày hội đọc sách" của trường lớp 7a; 7b; 7c đã chuẩn bị một số sách để trưng bày và giới thiệu. Biết số quyển sách của ba lớp này tỉ lệ nghịch với các số 5; 6; 8. Tính số sách của mỗi lớp, cho biết cả ba lớp chuẩn bị 59 quyển sách.

Tập hợp các chữ cái trong cụm từ “THÁI BÌNH" là:

A. {THAI; BINH}.

B. {T; H; A; I; B; N}.

C. {T; H; A; I; B; N; H}.

D. {T; H; A; I; B; I; N; H}.