7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 96)

Tìm x biết: x³ + 27 + (x + 3)(x – 9) = 0.

Phân tích các đa thức sau thành nhân tử: x³ – y³ + x – y.

Cho x + y = 3 và xy = 2. Tính x³ + y³.

Phân tích đa thức thành nhân tử: x³ + y³ + 2x² – 2xy + 2y².

Phân tích đa thức thành nhân tử: x⁴ – 25x² + 20x – 4.

Phân tích đa thức thành nhân tử: x⁴ + 6x³ – 11x² + 6x + 1.

Cho hàm số y = x⁴ + mx³ – 2x² – 3mx + 1. Xác định m để hàm số có 2 cực tiểu.

Phân tích đa thức x⁸ + x⁴ + 1 thành nhân tử ta được?

Tính $\frac{x-2}{x+1}.\frac{x^2-2x-3}{x^2-5x+6}$.

Tìm x biết x – 3 = (3 - x)².

Cho $f\left(x\right)=\frac{1}{3}\left(\frac{2x+4}{x^2}\right)$. Tìm $\underset{x\to 2}{\lim }f\left(x\right)$.

Cho $f\left(x\right)=\frac{1}{3}\left(\frac{2x+4}{x^2}\right)$. Tìm $\underset{x\to 2}{\lim }f\left(x\right)$.

Chứng minh A = n³ + (n + 1)³ + (n + 2)³ chia hết cho 9 với mọi n ∈ ℕ*.

Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Nếu $\underset{x\to x_0}{\lim }f\left(x\right)=-5$, $\underset{x\to x_0}{\lim }g\left(x\right)=0$ và g(x) > 0, ∀x ≠ x₀ thì $\underset{x\to x_0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}$ có kết quả nào sau đây?

A. -∞.

B. -5.

C. 0.

D. 5.

Cho dãy số (u_n) có số hạng tổng quát $u_n=\frac{2n+1}{n+2}$. Số $\frac{167}{84}$ là số hạng thứ mấy?

Xét tính bị chặn của dãy số (u_n) = $\frac{n^2+2n}{n^2+n+1}$.

Cho hàm số y = (m - 3)x + 3. Tìm các giá trị của m để hàm số nghịch biến trên ℝ.

Tìm GTLN và GTNN của hàm số $y=\frac{2\sin x+\cos x+3}{2\cos x-\sin x+4}$.

Tính đạo hàm của hàm số $y=\frac{\ln x+1}{\ln x-1}$.

Tìm giá trị lớn nhất M của hàm số y = sin2x + 2 cos²x.

Tìm GTNN và GTLN của hàm số: y = sinx + cosx.

Xem hình vẽ, cho biết a// b và c ⊥ a.

a) Đường thẳng c có vuông góc với đường thẳng b không? Vì sao?

b) Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết $\widehat{A_1}=115°$. Tính số đo các góc $\widehat{B_2};\widehat{B_3};\widehat{A_3}$

c) Gọi Ax và By lần lượt là tia phân giác của các góc $\widehat{A_1};\widehat{B_3}$. Chứng minh: Ax //By.

Xét sự biến thiên của hàm số $f\left(x\right)=\frac{-2}{x}$ trên khoảng (-∞; 0).

Tìm x, y nguyên biết xy + 3x – y = 6.

Xác định tọa độ đỉnh của parabol y = ax² + bx + c (a ≠ 0).

Tìm x biết x ∈ BC(15, 45) và x<200.

Cho các tập hợp A={x∈ℝ|x<3}, B={x∈ℝ |1<x≤5},C={x∈ℝ|−2≤x≤4}. Xác định (B∪C)\(A∩C).

Tìm x biết: x+(x+2)+(x+4)+...+(x+100)=2601.

Phân tích đa thức thành nhân tử: x² – 6x – y² + 9.

Tìm x biết: x² – 6x – 7 = 0.

Phân tích đa thức thành nhân tử: x³ – 2x² + 2x – 1.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N là trung điểm của SA và SB. Tìm giao tuyến (OMN) với (ABCD).

Tìm x biết x: 9 = 1325 dư 8.

Tìm x biết x⋮5và 13<x≤78.

Tìm x nhỏ nhất biết x chia hết cho 28; x chia hết cho 56; x chia hết cho 70 và 500< x <600.

Phân tích các đa thức thành nhân tử:

a) 3x²−12x+12.

b) x²+7x+7y−y².

Tìm x biết x thuộc B (4) và 16 ≤ x ≤28 (x ∈ℕ).

Với giá trị nào của m thì cặp số (2; -1) là 1 nghiệm của bất phương trình

2x−(m−2)y>3?

Tìm m để phương trình sau có nghiệm: 2cosx +1–m=0.

Cho hàm số y = (m + 5)x + 2m - 10. Với giá trị nào của m thì y là hàm số bậc nhất?

Chứng minh với mọi n ∈ ℕ^* thì 2n + 1 là số lẻ.

Vòng chung kết bóng đá tiểu học 2014, có 5 đội tuyển của 5 trường tham gia thi đấu theo thể thức vòng tròn 1 lượt. Đội thắng được 2 điểm, thua 0 điểm và nếu trận đấu có kết quả hòa thì mỗi đội được 1 điểm. Sau khi thi đấu người ta thấy tổng điểm của 5 đội là 21. Tính số điểm đội vô địch?

Viết dạng tổng quát của lũy thừa bậc n của số tự nhiên a. Công thức nhân hai lũy thừa cùng cơ số, chia hai luỹ thừa cùng cơ số.

Phát biểu và viết dạng tổng quát hai tính chất chia hết của một tổng. Phát biểu các dấu hiệu chia hết cho 2, cho 3, cho 5, cho 9.

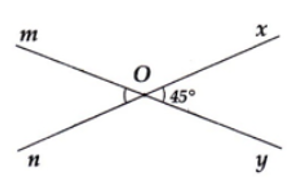
Cho góc $\widehat{xOy}$ có số đo bằng 45°. Vẽ hai tia Om, On lần lượt là tia đối của tia Oy, Ox. Tính số đo các góc còn lại trên hình.

Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số y=sin²x+2cos²x.

Viết các tập hợp: Ư(6), Ư(9), ƯC(6, 9).

Tìm cấp số nhân biết: $\left\{\begin{array}{l}{u}_1+u_2+u_3=14\\ u_1{u}_2{u}_3=64\end{array}\right.$.

Tìm các ước tự nhiên của 24.

Tìm ước chung lớn nhất của 77 và 126.

Bạn Kí đánh số trang sách bằng các số tự nhiên từ 1 đến 216. Bạn Kí phải viết tất cả bao nhiêu chữ số?

Từ ba tấm gỗ có độ dài 56 dm, 48 dm và 40 dm, bác thợ mộc muốn cắt thành các thanh gỗ có độ dài như nhau mà không để thừa mẩu gỗ nào. Hỏi bác cắt như thế nào để được các thanh gỗ có độ dài lớn nhất có thể?

Cho các mệnh đề P: “a và b chia hết cho c”;

Q: “a + b chia hết cho c”.

a) Hãy phát biểu định lý P ⇒ Q. Nêu giả thiết và kết luận của định lí và phát biểu định lí dưới dạng điều kiện cần, điều kiện đủ.

b) Hãy phát biểu mệnh đề đảo của mệnh đề P ⇒ Q rồi xác định tính đúng sai của mệnh đề đảo này.

Từ các chữ số 3, 1, 7 hãy viết tất cả các số có ba chữ số, mỗi số có cả ba chữ số đó rồi xếp các số theo thứ tự từ bé đến lớn.

Từ bốn chữ số 3; 4; 5; 0 hãy ghép thành các số tự nhiên có 3 chữ số khác nhau thỏa mãn:

a) Chia hết cho 3;

b) Chia hết cho 3 nhưng không chia hết cho 9.

1 ngọn hải đăng HB cao 150m so với mặt nước biển. Từ trên tàu biển, người lái tàu nhìn thấy đỉnh B của ngọn hải đăng.Biết $\widehat{BAH}$ = 10°.Tính khoảng cách từ tàu đến chân ngọn hải đăng?

Từ hai vị trí A và B người ta quan sát một cái cây (hỉnh vẽ). Lấy C là điểm gốccây, D là điểm ngọn của cây. A và B cùng thẳng hàng với H là điểm thuộc chiều cao CDcủa cây. Người ta đo được AB =10m, HC = 2m, góc $\widehat{A}$=60°; $\widehat{B}$ =45°. Tính chiều cao củacây.

Trong hộp có 45 quả bóng gồm 20 quả màu đỏ, 15 quả màu xanh và 10 quả màu vàng. Bạn lấy bao nhiêu quả bóng để chắc chắn có 3 quả bóng:

   a. Màu đỏ.

   b. Cùng màu.

   c. Khác màu.

Trong ngày đại hội thể dục thể thao, số học sinh của một trường khi xếp thành 12 hàng, 18 hàng và 21 hàng đều thừa 1 học sinh. Hỏi trường đó có bao nhiêu học sinh? (Biết số học sinh trong khoảng từ 500 đến 600).

Trung bình cộng của 10 số lẻ liên tiếp là 100. Tìm số lẻ lớn nhất trong 10 số lẻ đó.

Trường hợp nào sau đây chỉ tập hợp số tự nhiên?

A. {1;  2; 3; 4; …}.

B. {0; 1; 2; 3; 4; …}.

C. {0; 1; 2; 3; 4; …}.

D. {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.

Trục số là gì? Trục số dùng để làm gì?

Trong không gian cho đường thẳng a chứa trong mặt phẳng (P) và đường thẳng b song songvới mặt phẳng (P) . Mệnh đề nào sau đây là đúng?

A. a // b.

B. a, b không có điểm chung.

C. a, b cắt nhau.

D. a, b chéo nhau.

Trong mặt phẳng tọa độ Oxy, gọi (d) và (l) lần lượt là đồ thị của 2 hàm số $y=\frac{-1}{2}x+\frac{3}{2}$và $y=\left|x\right|$. Vẽ đồ thị (d) và (l) cắt nhau tại M và N. Chứng minh tam giác OMNvuông tại O.

Trong 1 lớp học có 40 học sinh trong đó có 30 học sinh đạt học sinh giỏi môn toán 25 học sinh đạt học sinh giỏi môn văn biết rằng chỉ có 5 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả 2 môn toán và văn hỏi có bao nhiêu học sinh chỉ học giỏi 1 trong 2 môn toán hoặc văn.

Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.

Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.

Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.

Chứng minh rằng trong n+1 số bất kỳ thuộc tập hợp {1; 2; 3; …; 2n} luôn chọn được 2 số mà số này là bội của số kia.

Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn 40 học sinh lớp 11 của trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi bạn quyên góp 2000đ, từ ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày liền trước là 500đ. Hỏi sau bao nhiêu ngày thì số tiền quyên góp được là 9800000đ.

Trong 1 hội nghị có 100 đại biểu tham dự, mỗi đại biểu nói được một hoặc hai trong ba thứ tiếng: Nga, Anh hoặc Pháp. Có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?

Một lô hàng có 10 sản phẩm, trong đó có 8 chính phẩm và 2 phế phẩm. Lấy tùy ý 6 sản phẩm từ lô hàng đó. Xét biến cố D: “Lấy 6 sản phẩm từ lô hàng và không có quá một phế phẩm”. Số kết quả thuận lợi của biến cố D là?

Chứng tỏ rằng: Trong ba số tự nhiên liên tiếp, có một số chia hết cho 3.

Trong buổi học kỹ năng sống ở Sóc Sơn, các bạn lớp 7A đã được hướng dẫncách dựng lều chữ A (dạng hình lăng trụ đứng có đáy là tam giác đều) từ một tấm vảibạt cho trước.

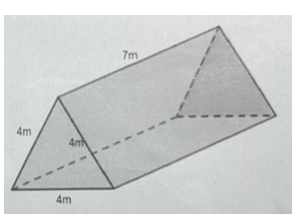
a) Tính diện tích vải bạt cần sử dụng để làm hai mái và trải đáy của lều, biếtkích thước lều như trên hình vẽ.

b) Nếu giáo viên lớp chuẩn bị được tấm vải bạt dài 15m rộng 7m thì tấm vảibạt cần thêm diện tích là bao nhiêu đủ để làm hai mái và trải đáy của lều?

Trong các hàm số sau hàm số nào là hàm số chẵn:

A. y = sin2x.

B. y = cos3x.

C. y = cot4x.

D. y = tan5x.

Trong các hàm số sau hàm số nào là hàm số chẵn:

A. y = -sinx.

B. y = cosx – sinx.

C. y = cosx + sin²x.

D. y = cosx.sinx.

Trong các phát biểu sau, phát biểu nào về khối tròn xoay là không đúng?

A. Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được hình cầu.

B. Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình trụ.

C. Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được hình tròn.

D. Khi quay hình tam giác vuông một vòng quanh một góc vuông cố định, ta được hình nón.

Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.

Trong hộp có 100 viên bi,an và nam chơi trò chơi như sau mỗi lần chơi được bốc k viên bi ( 0<k<11).Người bốc bi ở lượt chơi cuối cùng là người thắng cuộc. Chứng minh rằng ai đi trước là người có chiến thuật để dành chiến thắng

Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ số 3 kim phút OP chỉ số 12. Đến khi kim phút và kim giờ gặp nhau lần đầu tiên. Tính số đo góc lượng giác mà kim giờ quét được?

Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):y=mx+5. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P):y=x² tại hai điểm phân biệt có hoành độ lần lượt là x₁, x₂với x₁<x₂) sao cho |x₁|>|x₂|.

Cho hàm số y=f(x) xác định, liên tục trên Rℝ và có bảng biến thiên sau

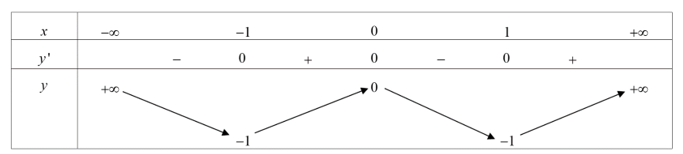
Tìm tất cả các giá trị thực của tham số m để phương ctrình f(x)=m vô nghiệm.

Trên tiếp tuyến của đường tròn (O,R) tại a lấy 1 điểm P sao cho $AP=R\sqrt{3}$.

a) Tính các caạnh và các góc của tam giác PAO.

b) Kéo dài đường cao AH của tam giác PAO cắt đường tròn O tại B. Chứng minh BP là tiếp tuyến đường tròn (O).

Tìm 3 số thập phân x thỏa mãn 35,82 < x < 35,83.

Tổng của hai số là 407 . Biết $\frac{1}{4}$ của số thứ 1 thì bằng $\frac{1}{7}$ của số thứ 2. Tìm 2 số đó.

Tính nhanh S = 1 + 4 + 7 + ... + 2008.

Cho hai tập hợp A=[m-4;1], B=(-3;m]. Tính tổng tất cả các giá trị nguyên của m để A∪B=B.

Cho 2 tập hợp M=[2m−1;2m+5] và N=[m+1;m+7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.

Tính tổng tất cả các số có ba chữ số khác nhau mà các chữ số đều lẻ.

Một hộp có 5 viên bi đỏ, 4 viên bi trắng. Chọn ngẫu nhiên 2 viên bi. Xác suất 2 viên bi được chọn có đủ hai màu là?

Tính nhanh $\frac{1}{1.2}+\frac{1}{2.3}+\mathrm{...}+\frac{1}{9.10}$.