40 câu hỏi
Miền nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 là nửa mặt phẳng chứa điểm:
(3; 0).
(3; 1).
(3; 2)
(0; 0).
Trong các mệnh đề mệnh đề nào sai?
Phép dời là phép đồng dạng tỉ số k = 1.
Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.
Phép đồng dạng bảo toàn tỉ số góc.
Hệ bất phương trình \(\left\{ \begin{array}{l}\left( {x + 3} \right)\left( {4 - x} \right) > 0\\x < m - 1\end{array} \right.\) vô nghiệm khi:
m ≤ –2
m > –2
m < –1
m = 0.
Tìm tất cả các giá trị của tham số m để bất phương trình mx + 4 > 0 nghiệm đúng với mọi |x| < 8.
\(m \in \left[ {\frac{{ - 1}}{2};\frac{1}{2}} \right]\)
\(m \in \left( { - \infty ;\frac{1}{2}} \right]\)
\(m \in \left[ { - \frac{1}{2}; + \infty } \right)\)
\(m \in \left[ { - \frac{1}{2};0} \right) \cup \left( {0;\frac{1}{2}} \right]\).
Trong một hộp bút có 2 bút đỏ, 3 bút đen và 2 bút chì. Hỏi có bao nhiêu cách để lấy một cái bút?
12.
6.
2.
7
Cho hình bình hành ABCD tâm O. Khi đó \(\overrightarrow {OB} - \overrightarrow {OA} \) bằng:
\(\overrightarrow {OC} + \overrightarrow {OB} \)
\(\overrightarrow {BA} \)
\(\overrightarrow {OC} + \overrightarrow {OD} \)
\(\overrightarrow {CD} \).
Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố “Lấy lần thứ hai được một viên bi xanh”, ta được kết quả:
\(\frac{5}{8}\)
\(\frac{5}{9}\)
\(\frac{5}{7}\)
\(\frac{4}{7}\).
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1; 2; –1); B(2; –1; 3); C(–3; 5; 1). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
D (–4; 8; –5)
D (–4; 8; –3)
D (–2; 8; –3)
D (–2; 2; 5).
Cho hàm số đa thức f(x) có đạo hàm trên R. Biết f(0) = 0 và đồ thị hàm số y = f’(x) như hình sau:
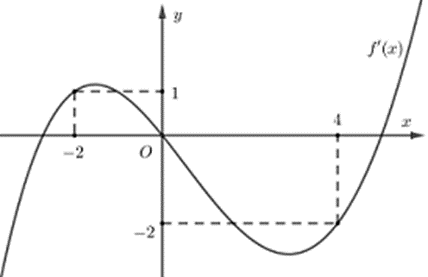
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2}} \right|\) đồng biến trên khoảng nào dưới đây?
(4; +∞)
(0; 4)
(–∞; –2)
(–2; 0).
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) có hai nghiệm thực phân biệt?
3
vô số
4
5
Trong mặt phẳng tọa độ Oxy cho đường thẳng d: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay –90°.
d’: x + 3y + 2 = 0.
d’: x + 3y – 2 = 0.
d’: 3x – y – 6 = 0.
d’: x – 3y – 2 = 0.
Trong 2019 điểm phân biệt cho trước, có bao nhiêu vectơ khác \(\overrightarrow 0 \) với điểm đầu và điểm cuối là 2 trong 2019 điểm đã cho?
\(C_{2019}^2\)
20192
\[{\rm{A}}_{2019}^{2017}\]
\[{\rm{A}}_{2019}^2\].
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{{2{\rm{x}} + 1}}{{\sqrt {{x^2} - 6{\rm{x}} + m - 2} }}\) xác định trên ℝ.
m ≥ 11
m > 11
m < 11
m ≤ 11.
Cho hình bình hành ABCD. M là điểm bất kì, khi đó:
\(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {MB} - \overrightarrow {M{\rm{D}}} \)
\(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {DA} - \overrightarrow {{\rm{DC}}} \)
\(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AB} + \overrightarrow {{\rm{AD}}} \)
\(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {BA} - \overrightarrow {BC} \).
Có 5 nam, 5 nữ xếp thành một hàng dọc. Tính xác suất để nam, nữ đứng xen kẽ nhau.
\(\frac{1}{{125}}\)
\(\frac{1}{{126}}\)
\(\frac{1}{{36}}\)
\(\frac{{13}}{{36}}\).
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau:
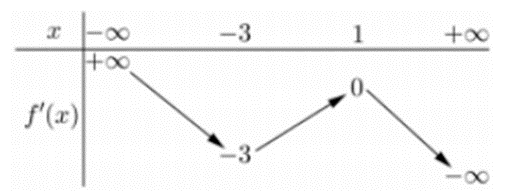
Bất phương trình f(x) < ex + m đúng với mọi x ∈ (–1; 1) khi và chỉ khi:
m ≥ f(1) – e
\(m > f\left( { - 1} \right) - \frac{1}{e}\)
\(m \ge f\left( { - 1} \right) - \frac{1}{e}\)
m > f(1) – e .
Cho hàm số \(y = \frac{{ax + b}}{{c{\rm{x}} - 1}}\) có đồ thị như hình vẽ bên dưới. Giá trị của tổng S = a + b + c bằng:
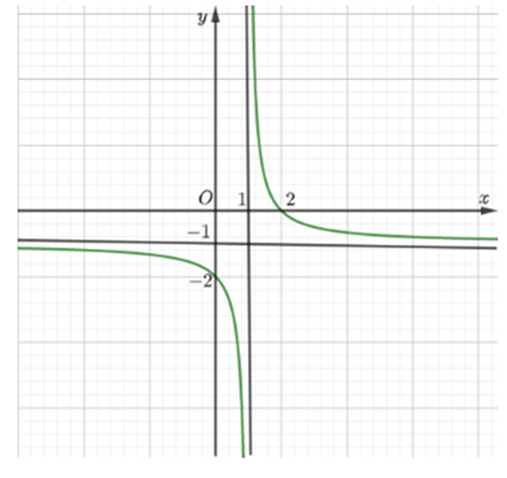
S = 0
S = –2
S = 2
S = 4.
Cho 4 điểm A(1; –2), B(0; 3), C(–3; 4), D(–1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
A, B, C
B, C, D
A, B, D
A, C, D.
Cho tam giác ABC có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
2
3
4
6.
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn BC, đáy nhỏ AD. Mặt bên (SAD) là tam giác đều, (α) là mặt phẳng đi qua M trên cạnh AB, song song với SA, BC. Mp (α) cắt các cạnh CD, SC, SB lần lượt tại N, P, Q. Tứ giác MNPQ là hình gì?
Hình thoi
Hình bình hành
Tứ giác có các cạnh đối cắt nhau
Hình thang cân.
Một thầy giáo có 12 cuốn sách đôi một khác nhau, trong đó có 5 cuốn sách văn học, 4 cuốn sách âm nhạc và 3 cuốn sách hội họa. Thầy muốn lấy ra 6 cuốn và đem tặng cho 6 học sinh mỗi em một cuốn. Thầy giáo muốn rằng sau khi tặng xong, mỗi một trong 3 thể loại văn học, âm nhạc, hội họa đều còn lại ít nhất một cuốn. Hỏi thầy có tất cả bao nhiêu cách tặng?
665 280
85 680
119
579 600.
Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:
\(\frac{2}{5}\)
\(\frac{1}{{10}}\)
\(\frac{3}{5}\)
\(\frac{1}{{20}}\).
Tính \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + 2{\rm{x}}} \cdot \sqrt[3]{{1 + 3{\rm{x}}}} \cdot \sqrt[4]{{1 + 4{\rm{x}}}} - 1}}{x}\).
\(\frac{{23}}{2}\)
24
\(\frac{3}{2}\)
3.
Một con súc sắc đồng chất được gieo 6 lần. Xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là:
\(\frac{{31}}{{23328}}\)
\(\frac{{41}}{{23328}}\)
\(\frac{{31}}{{23328}}\)
\(\frac{{21}}{{23328}}\).
Rút gọn biểu thức \(P = {x^{\frac{1}{3}}}.\sqrt[6]{x}\), x > 0.
P = x2
\(P = \sqrt x \)
\(P = {x^{\frac{1}{8}}}\)
\(P = {x^{\frac{2}{9}}}\).
Trong hệ tọa độ Oxy, cho điểm M (3; –4). Gọi M1, M2 lần lượt là hình chiếu vuông góc của M trên Ox, Oy. Khẳng định nào đúng?
\(\overline {O{M_1}} = - 3\)
\(\overline {O{M_2}} = 4\)
\(\overrightarrow {O{M_1}} - \overrightarrow {O{M_2}} = \left( { - 3; - 4} \right)\)
\(\overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = \left( {3; - 4} \right)\)
Tìm hệ số của số hạng chứa x10 trong khai triển của biểu thức \({\left( {3{{\rm{x}}^3} - \frac{2}{{{x^2}}}} \right)^5}\).
–810
826
810
421.
Cho x là số thực dương, số hạng chứa x trong khai triển\({\left( {x + \frac{2}{{\sqrt x }}} \right)^4}\)là:
24x
12x
24
12.
Phương trình tiếp tuyến của đồ thị \(y = \frac{{2{\rm{x}} - 1}}{{x - 1}}\) tại điểm A(2; 3) là:
y = –3x + 9
y = –x + 5
y = 3x – 3
y = x + 1
Cho hàm số y = f(x) xác định trên R\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
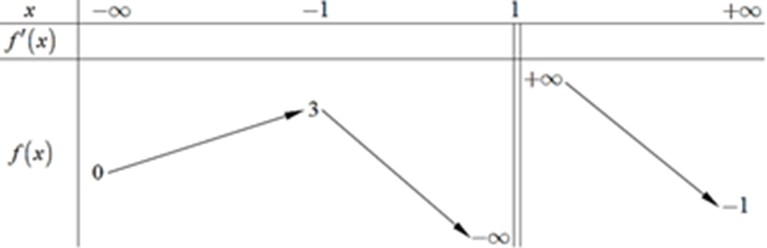
Số giá trị nguyên của tham số m để phương trình f(x) = m có 3 nghiệm phân biệt là
1
0
3
2.
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng (α) đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số \(\frac{{SN}}{{S{\rm{D}}}}\) để (α) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
\(\frac{1}{2}\)
\(\frac{1}{3}\)
\(\frac{{\sqrt 5 - 1}}{2}\)
\(\frac{{\sqrt 3 - 1}}{2}\).
Cho tanα = 2. Tính giá trị của biểu thức \(G = \frac{{2\sin \alpha + cos\alpha }}{{cos\alpha - 3\sin \alpha }}\).
G = 1
\(G = \frac{{ - 4}}{5}\)
\(G = \frac{{ - 6}}{5}\)
G = –1.
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Hai đường thẳng cắt nhau.
Ba điểm phân biệt
Bốn điểm phân biệt
Một điểm và một đường thẳng.
Gieo ba con súc sắc. Xác suất để được nhiều nhất hai mặt 5 là.
\(\frac{5}{{72}}\)
\(\frac{1}{{216}}\)
\(\frac{1}{{72}}\)
\(\frac{{215}}{{216}}\).
Cho phương trình \(\log _2^2x - 2{\log _2}x - \sqrt {m + {{\log }_2}x} = m\) (*). Có bao nhiêu giá trị nguyên của tham số m ∈ [–2019; 2019] để phương trình (*) có nghiệm?
2021
2019
4038
2020.
Bất phương trình \({\log _{\frac{2}{3}}}\left( {2{{\rm{x}}^2} - x - 1} \right) > 0\) có tập nghiệm là (a; b) ∪ (c; d). Tính tổng a + b + c + d.
\(\frac{3}{2}\)
0
1
\( - \sqrt {17} \).
Cho tam giác ABC và đặt \(\overrightarrow a = \overrightarrow {BC} ,\overrightarrow b = \overrightarrow {AC} \). Cặp vectơ nào sau đây cùng phương:
\(2\overrightarrow a + \overrightarrow b ,\overrightarrow a + 2\overrightarrow b \)
\(2\overrightarrow a - \overrightarrow b ,\overrightarrow a - 2\overrightarrow b \)
\(5\overrightarrow a + \overrightarrow b , - 10\overrightarrow a - 2\overrightarrow b \)
\(\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b \).
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a và \[{\rm{AA}}' = a\sqrt 2 \]. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:
\[\frac{{\pi {a^3}}}{3}\]
\(\pi {a^3}\)
\[\frac{{4\pi {a^3}}}{3}\]
\(4\pi {a^3}\).
Trong mặt phẳng (Oxy) cho A(1; 2), B(4; 1), C(5; 4). Tính \(\widehat {BAC}\).
60°
45°
90°
120°.
Cho α và β là hai góc nhọn bất kỳ thỏa mãn α + β = 90°. Khẳng định nào sau đây là đúng?
tanα = sinβ
tanα = cotβ
tanα = cosα
tanα = tanβ.