7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 76)

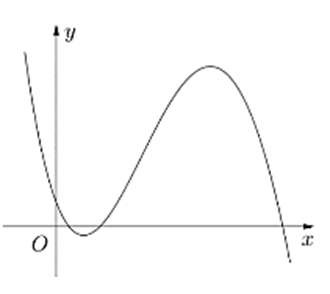
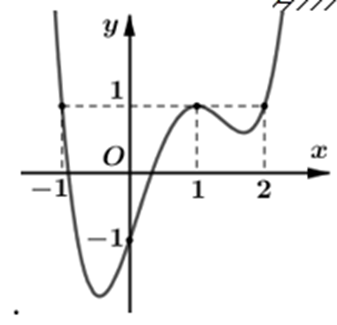
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ dưới đây. Tìm số nghiệm của phương trình f(x) = 3. 

Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.

Tìm chu kì của hàm số \[y = \sin \sqrt x \].

Điều kiện để hàm số bậc ba không có cực trị là phương trình y’ = 0 có:

Cho hàm số: y = x⁴ + 2mx² + 9. Tìm m để hàm số cắt trục hoành tại 4 điểm phân biệt.

Tìm m để đồ thị hàm số y = x³ − 3x² + mx có hai điểm cực trị A và B đối xứng nhau qua đường thẳng x − 2y − 5 = 0.

Đồ thị hàm số y = −x³ + 3mx² – 3, có cực đại và cực tiểu đối xứng nhau qua đường thẳng d : x + 8y − 74 = 0 khi m bằng.

Cho chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a. CD = a. Góc giữa 2 mặt phẳng (SBC) và (ABCD) bằng 60º. Gọi I là trung điểm của cạnh AD. Biết 2 mặt phẳng ( SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích của khối chóp S.ABCD theo a.

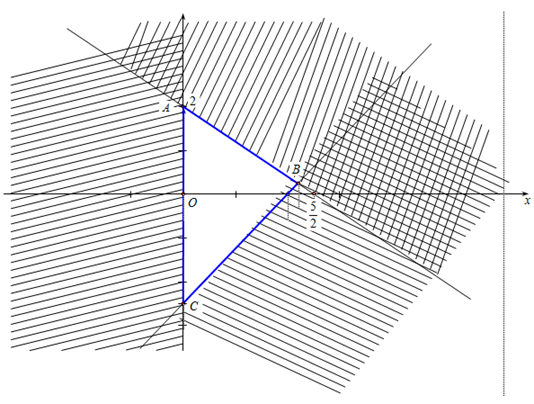
Chứng minh miền tam giác ABC (như hình vẽ) là miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x \ge 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\].

Giá trị nhỏ nhất của biểu thức \[B = \sqrt {4{a^2} - 4a + 1} \; + \;\sqrt {4{a^2} - 12a + 9} \].

Rút gọn biểu thức: \[A = \frac{{\sqrt x }}{{\sqrt x - 5}} - \frac{{10\sqrt x }}{{x - 25}} - \frac{5}{{\sqrt x + 5}}\] (x ≥ 0; x ¹ 25)

Rút gọn biểu thức:

\[A = \frac{{x - 2\sqrt x }}{{x\sqrt x - 1}} + \frac{{\sqrt x + 1}}{{x\sqrt x + x + \sqrt x }} + \frac{{1 + 2x - 2\sqrt x }}{{{x^2} - \sqrt x }}\] (x > 0, x ¹ 1)

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{{{(x + y)}^2}\left( {8{x^2} + 8{y^2} + 4xy - 13} \right) + 5 = 0}\\{2x + \frac{1}{{x + y}} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Giải hệ phương trình:\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\].

Cho tam giác ABC đều. Mệnh đề nào sau đây sai?

Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \[\widehat {BAC} = 120^\circ \]. Tính bán kính mặt cầu ngoại tiếp lăng trụ trên.

Phát biểu mệnh đề phủ định của mệnh đề: “13 là số nguyên tố”

Xét tính đúng sai của các mệnh đề “2020 chia hết cho 3” và phát biểu mệnh đề phủ định của nó.

Trong một cuộc thi chạy 1000 m, khi An về đích thì Bình cách đích 40 m, Cường còn cách đích 100 m. Hỏi nếu Cường và Bình giữ nguyên vận tốc thì khi Bình về đích thì Cường còn cách đích bao nhiêu?

Cho tam giác ABC có a² = b² + c² − bc. Tính số đo của góc A.

Giải phương trình: \[\sqrt {5{x^2} + 4x} - \sqrt {{x^2} - 3x - 18} = 5\sqrt x \].

Giải phương trình: \[{x^2} + 6x + 1 = (2x + 1)\sqrt {{x^2} + 2x + 3} \].

Giải phương trình:sin² x + 2sin x – 3 = 0.

Giải phương trình: 4sin³ x + 3cos³ x – 3sin x – sin² xcos x = 0.

Rút gọn biểu thức: \[3\sqrt 5 a - \sqrt {20} a + 4\sqrt {45} a + \sqrt a \] với a ≥ 0.

Rút gọn biểu thức: \[5\sqrt {\frac{1}{5}} + \frac{1}{{20}}\sqrt {20} + \sqrt 5 \].

Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh của hình nón đó.

Hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 10a. Tính thể tích của khối trụ đã cho.

Tìm cực trị của hàm số y = 2x³ – 6x + 2.

Điền dấu thích hợp vào chỗ chấm: 9m50cm…905 cm.

Điền số thích hợp vào chỗ chấm:

40 m/s = …. km/h.

Cho hai tập hợp: \[A = \left( { - \infty ;\,\,m} \right)\] và \[B = \left( {2;\, + \infty } \right)\]. Tìm tất cả các giá trị thực của tham số m để \[A \cup B = \mathbb{R}\].

Cho hai tập hợp: \[A = \left\{ {x \in \mathbb{R}|1 \le \left| x \right| \le 2} \right\};\,\,B = \left( { - \infty ;m - 2} \right)\, \cup \left[ {m; + \infty } \right)\]. Tìm tất cả các giá trị thực của tham số m để \[A \subset B\].

Cho A = (m; m + 1); B = (1;4). Tìm m để \[A \cap B \ne \emptyset \].

Cho tập hợp khác rỗng \[A = ( - \infty ;m)\] và B = [2m – 2; 2m + 2]. Tìm \[m \in \mathbb{R}\] để \[({C_\mathbb{R}}A) \cap B \ne \emptyset \].

Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?

Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:

- Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.

- Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A và B.

Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \[\frac{1}{2}\]  số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Tìm phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất.

Cho phương trình: x² – 4x + m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x₁, x₂ thỏa mãn: x₁³ + x₂³ – 5(x₁² + x₂²) = 26.

Cho phương trình: x² – 4x + m + 1 = 0. Tìm m để phương trình có 2 nghiệm phân biệt x₁, x₂ thỏa mãn: x₁² + x₂² = 12.

Trong mặt phẳng Oxy cho hai điểm A(1;6), B(−1; −4). Gọi C, D lần lượt là ảnh của A và B qua phép dời hình \[\left\{ \begin{array}{l}x' = x + 1\\y' = y + 5\end{array} \right.\]. Chứng minh bốn điểm A, B, C, D thẳng hàng.

Trong mặt phẳng tọa độ Oxy cho điểm M(2;3). Tìm ảnh của điểm M qua phép đối xứng trục Ox.

Trong mặt phẳng tọa độ Oxy cho điểm A(3;5). Tìm ảnh của điểm M qua phép đối xứng trục Oy.

Trong mặt phẳng tọa độ Oxy nếu phép tịnh tiến biên M(4;2) thành M′(4;5) thì nó biến điểm A(2;5) thành điểm có toạ độ là bao nhiêu?

Nếu phép tịnh tiến biến điểm A(1;2) thành điểm A′(−2;3) thì nó biến điểm B(0;1) thành điểm nào?

Tìm m để hai đồ thị hàm số y = 2x – 1 và y’ = –x + m cắt nhau tại 1 điểm có hoành độ bằng 2.

Tìm giá trị thực của tham số m để phương trình 9^x −2.3^x+1 + m = 0 có hai nghiệm thực x₁, x₂  thỏa mãn x₁ + x₂ = 0.

Tìm các giá trị thực của tham số m để phương trình (m – 1)x² – 2mx + m = 0 có một nghiệm lớn hơn 1 và một nghiệm nhỏ hơn 1.

Trong mặt phẳng toạ độ Oxy, gọi d là đường phân giác của góc phần tư thứ hai. Phép đối xứng trục D_d biến điểm P(5;−2) thành điểm P’ có toạ độ bao nhiêu?

Cho hàm số y = −x³ + 3mx² − 3m − 1 = 0 với m là tham số thực. Tìm m để đồ thị hàm số đã cho có hai điểm cực trị A và B đối xứng nhau qua đường thẳng d: x + 8y – 74 = 0.

Tìm nghiệm của phương trình cos x = −1.

Cho B = [3;+∞), C = (−∞;−2). Tìm B Ç C.

Có bao nhiêu cách sắp xếp 20 thí sinh vào một phòng thi có 20 bàn mỗi bàn một thí sinh.

Trong kì thi THPT Quốc Gia, mỗi phòng thi gồm 24 thí sinh được sắp xếp vào 24 bàn khác nhau. Bạn Nam là một thí sinh dự thi, bạn đăng kí 4 môn thi và cả 4 lần đều thi tại 1 phòng duy nhất. Giả sử giám thị xếp thí sinh vào vị trí một cách ngẫu nhiên, tính xác suất để trong 4 lần thi thì bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí.

Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn. Qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C, D. Chứng minh rằng CD = AC + BD, \[\widehat {COD} = 90^\circ \].

Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax, By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn. Qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C, D. Chứng minh rằng AC. BD = R².

Cho góc \[\widehat {xOy}\] lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao điểm của AB với tia phân giác của góc \[\widehat {xOy}\]. Chứng minh rằng: AK = KB.

Cho góc \[\widehat {xOy}\] lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao điểm của AB với tia phân giác của góc \[\widehat {xOy}\]. Chứng minh rằng: OK ^ AB.

Cho 2 tập hợp \[A = \left\{ {x \in \mathbb{R}|\left| x \right| > 4} \right\},\,\,B = \left\{ {x \in \mathbb{R}| - 5 \le x - 1 < 5} \right\}\].

Tìm A Ç B.

Cho sin x + cos x = m. Tính theo m giá trị của M = sin x.cos x.

Tìm nghiệm của phương trình nằm trong \[\left[ {0;2\pi } \right)\].

sin 2x + sin x = 0

Cho các chữ số 1; 2; 3; 4; 5. Hỏi có bao nhiêu số có 4 chữ số được lập từ các chữ số trên?

Một người chạy bộ theo đường thẳng AB = 50 m, từ A đến B rồi quay về A. Gốc toạ độ O ở trong khoảng AB, cách A một khoảng 10 m, chiều dường từ A đến B. Tính độ dời từ A khi người này đến O.

Cho hàm số y = ax³ + bx² + cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?

Với các chữ số 0; 1; 2; 3; 4; 5 ta lập được bao nhiêu số có 8 chữ số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt đúng 1 lần?

Cho B_n là tập hợp các số nguyên là bội số của n. Tìm sự liên hệ giữa m và n sao cho B_n ⊂ B_m .

Trong 100 học sinh lớp 10, có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được tiếng Anh và tiếng Pháp?

Lớp 6A có \[\frac{4}{5}\] số học sinh yêu thích môn Toán, \[\frac{7}{{10}}\] số học sinh yêu thích môn ngữ văn, \[\frac{{12}}{{25}}\] số học sinh yêu thích môn Tiếng anh. Hỏi trong 3 môn học trên môn học nào được các bạn lớp 6A thích nhất?

Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.

Cho hai tập hợp:

A = {1; 3}; B = {1; 2}

Tìm A ∪ B ; A ∩ B ; A \ B ; B \ A.

Tìm giá trị thực của tham số mđể đường thẳng d: y = (2m − 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x³ − 3x² + 1.

Tìm m để đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1.

Tìm giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ bất phương trình \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\].

Có 6 học sinh và 3thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách xếp chỗ ngồi cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh?

Có bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau sao cho trong mỗi số đều có mặt các chữ số 8 và 9?

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA⊥(ABC) góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng AC và SB.

Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của (SAB)  và (SCD).

Tìm tập xác định D của hàm số y = log₂ (x² + 5x − 6).

Tìm tập xác định D của hàm số y = log₂(x³ − 8)¹⁰⁰⁰ .

Cho hàm số y=f(x) xác định trên ℝ\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

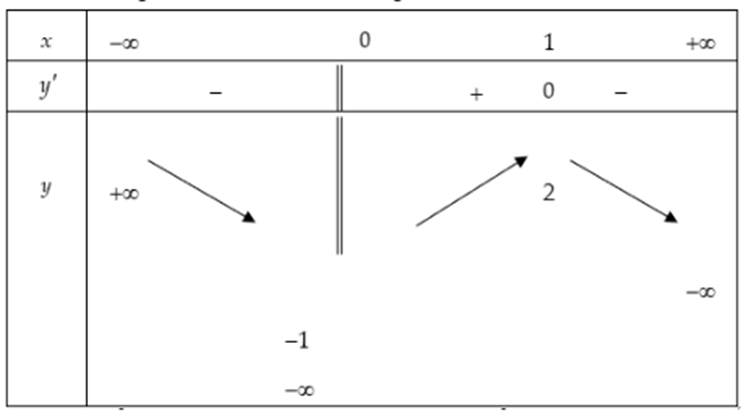
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm thực phân biệt.

Tìm số điểm biểu diễn các nghiệm của phương trình \[\sin \left( {2x + \frac{\pi }{3}} \right) = \frac{1}{2}\]trên đường tròn lượng giác.

Cho hàm số \[y = \frac{{mx - 2m - 3}}{{x - m}}\]   với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.

Tìm tất cả các giá trị của tham số m để hàm số \[y = {\log _{2020}}(mx - m + 2)\]xác định trên \[[1; + \infty )\].

Tính tích tất cả các nghiệm của phương trình \[\log _3^2x - 2{\log _3}x - 7 = 0\].

Giải phương trình sau: log₂(x² + x + 2) = 3.

Rút gọn biểu thức C = 6x(x + 3x −1) − 6x² − 8xy

Rút gọn biểu thức: A = 2x²(− 3x³ + 2x² + x − 1) + 2x(x² – 3x + 1)

Tìm m để hệ phương trình sau vô nghiệm:\[\left\{ \begin{array}{l}x - my = m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\mx - 9y = m + 6\,\,\,\,\,(2)\end{array} \right.\]

Tìm m để hệ phương trình sau vô số nghiệm:

\[\left\{ \begin{array}{l}2x + my = m + 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\(m + 1)x + 2my = 2m + 4\,\,\,\,\,\,\,(2)\end{array} \right.\]

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB)và (SCD).

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Bằng cách tính, hãy so sánh hai số 2³ và 3².

Viết gọn tích sau dưới dạng lũy thừa:

a) 2.4.8.8.8;

b) x.x.x.x.x.

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.

+ Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;

+ Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x – y + 1 = 0. Để phép tịnh tiến theo vectơ \[\overrightarrow v \] biến d thành chính nó. Tìm \[\overrightarrow v \].

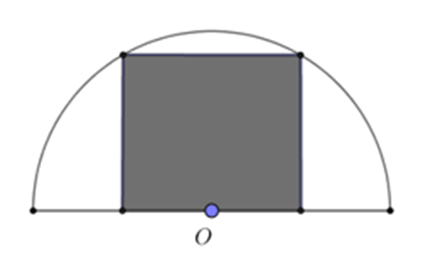
Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1 m, người ta cắt ra một hình chữ nhật (phần tô đậm như hình vẽ). Tính diện tích lớn nhất có thể cắt được của phần hình chữ nhật.

Phát biểu định lý Talet.

Hình nào sau đây không có tâm đối xứng?

Tìm tập xác định của hàm số \[y = \frac{1}{{\sin \,\,2x}}\].

Tìm điều kiện của hàm số \[y = \frac{{3\sqrt {\sin \,x} }}{{\cos x + 1}}\].

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD bằng \[\frac{{4{a^3}}}{3}\]. Gọi α là góc giữa SC và mặt đáy. Tính tan α.

Tính đạo hàm của hàm số tại điểm x₀ sau:

y = 7 + x – x², với x₀ = 1.

Tính các đạo hàm của hàm số sau:y = (2x – 3)(x⁵ – 2x)

Cho các tập hợp: \[A = ( - \infty ;m)\] và B = [3m – 1; 3m + 1]. Tìm giá trị m để A Ç B = Æ.

Trong hệ tọa độ Oxy cho tam giác ABC có A(3; 5); B(1; 2) và C(5; 2). Tìm tọa độ trọng tâm G của tam giác ABC?

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB và O là 1 điểm tùy ý. Chứng minh rằng: \[\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \].

Xác định miền nghiệm của bất phương trình: 2x – y ≥ 0.

Có bao nhiêu số tự nhiên có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?

Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD. Hãy xác định giao tuyến của hai mặt phẳng (IJM) và (ACD).

Tính độ dài đoạn thẳng AB với A( (2;1;0), B(4; −1;1).

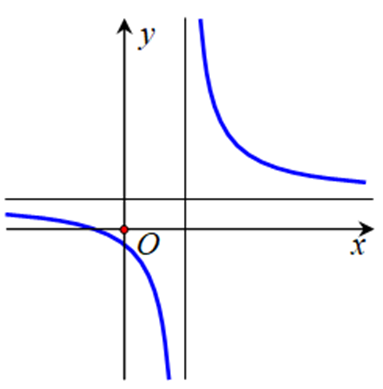
Đồ thị hàm số \[y = \frac{1}{x}\] có mấy đường tiệm cận ngang?

Chứng minh đồ thị hàm số \[y = \frac{{{x^2} - 2x}}{{x - 1}}\]không có tiệm cận ngang.

Tìm giá trị lớn nhất của biểu thức: \[A = \frac{{ab}}{{a + b}} + \frac{{bc}}{{b + c}} + \frac{{ac}}{{a + c}}\].

Biết a + b + c = 6.

Tính đạo hàm của hàm số: y = (1 + 2x)(2 + 3x²)(3 – 4x³)

Tính đạo hàm của hàm số sin²x?

Hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?

Trong mặt phẳng Oxy cho đường thẳng d có phương trình: x + y + 2 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng tâm I(1;0).

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x − 6y + 5 = 0, điểm I(2; −4). Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm I.

Cho biểu thức A = 1 + 3 + 3² + 3³ + 3⁴ + ….+ 3⁹⁹. Chứng minh rằng: A chia hết cho 4.

Cho biểu thức B = 1 + 4 + 4² + 4³ + 4⁴ + ….+ 4⁵⁰. Chứng minh rằng: B chia hết cho 21.

Trong các khẳng định sau, khẳng định nào đúng?

Trong mặt phẳng Oxy, tìm ảnh của điểm M(−6;1) qua phép quay Q(O; 90°).

Hàm số y = x³ − 3x + 2 đồng biến trên khoảng nào?

Hàm số y = x³ – 3x² + 2 nghịch biến trên khoảng nào?

Cho hàm số y = sin x – 3cos x. Tính vi phân của hàm số.

Cho hàm số \[y = \frac{x}{{{x^2} + 1}}\].Tính vi phân của hàm số.

Chứng minh \[1 + tanx + ta{n^2}x + ta{n^3}x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}{{{{\cos }^3}x}}\].

Chứng minh đẳng thức: (1 + sin x)(cot x – cos x) = cos³ x.

Tính bán kính đường tròn ngoại tiếp hình vuông cạnh bằng 1.

Cho hàm số \[y = \frac{{x - 2}}{{x - 1}}\]. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp điểm M là giao điểm của đồ thị hàm số với trục tung.

Cho hàm số y = log₂x. Khẳng định nào sau đây sai?

Gieo đồng xu cân đối và đồng chất 5 lần liên tiếp. Tính xác suất để được ít nhất một lần xuất hiện mặt sấp.

Cho hai góc nhọn α và β (α < β). Khẳng định nào sau đây là sai?

Cho hàm số y = x³ + 3x² – 9x – 7. Khẳng định nào sau đây là khẳng định sai?

Cho hàm số f(x) xác định trên \[\mathbb{R}\] và có đồ thị f'(x) như hình vẽ bên dưới. Tìm giá trị nhỏ nhất của hàm số g(x) = f(2x) − 2x + 1 trên đoạn \[\left[ { - \frac{1}{2};1} \right]\].

Cho biết \[\tan \,\alpha = \frac{1}{2}\]. Tính cot a.

Chứng minh sin⁶ x + cos⁶ x = 1 − 3sin² x.cos² x.

Tìm tập xác định D của hàm số:

\[y = {\log _{2019}}\left( {4 - {x^2}} \right) + {\left( {2x - 3} \right)^{ - 2019}}\]

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, \[AB = a\sqrt 5 \], AC = a.. Cạnh bên SA = 3a và vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABC.

Giải phương trình sau: cos² x – sin 2x = 0.

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Gọi H là hình chiếu của A trên SB. Tính khoảng cách giữa AH và BC.

Cho a là góc tù và \[\sin \alpha = \frac{4}{5}\]. Tính giá trị của biểu thức: A = 2sin a – cos a.

Cho a là góc nhọn và \[\sin \alpha = \frac{3}{5}\]. Tính giá trị của biểu thức:

A = 3sin a – 2cos a.

Cho \[\sin \alpha = \frac{2}{3}\]. Tính cos α, tan α biết 0 < α < 90º.

Tính các tỉ số lượng giác sau:

a) cos 60º

b) tan 30º

c) sin 45º

d) cot 135º

Tìm tất cả các giá trị thực của tham số m để hàm số y = log(x² − 2mx + 4) có tập xác định là \[\mathbb{R}\].

Một máy bay đang bay ở độ cao 12 km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất. Nếu cách sân bay 320 km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

Tính các giá trị lượng giác còn lại của góc α biết \[\sin \,\alpha = \frac{1}{3}\] và 90° < α < 180°.

Cho bất phương trình \[4\sqrt {(x + 1)(3 - x)} \le {x^2} - 2x + m - 3\]. Xác định m để bất phương trình nghiệm đúng với ∀x ∈ [−1; 3].

Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số cắt đường thẳng (d’): y = 2x + 1 tại điểm có hoành độ bằng –2.

Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m):                 

y = 0,5x – 3.

Tính các giá trị lượng giác sau: sin 570º, cos (−1035º), tan 1500º

Cho hàm số y = f(x) có đồ thị như hình vẽ. Phương trình f[f(cos x) − 1] = 0 có bao nhiêu nghiệm trên đoạn [0;2π]?

Tính \[\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {x + 2} - 2}}{{x - 2}}\] \[(k \in \mathbb{Z})\].

Tìm số nghiệm của phương trình sin x = 0 trên đoạn [0;π].

Nêu khái niệm phép đồng dạng.

Phép vị tự là gì?

rong mặt phẳng tọa độ Oxy, cho \[\overrightarrow v \] = (1; −3) và đường thẳng d có phương trình 2x − 3y + 5 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến \[{T_{\overrightarrow v }}\] .

Trong mặt phẳng Oxy, cho điểm M(2;3). Tìm điểm là ảnh của M qua phép đối xứng qua đường thắng d: x − y = 0.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA ⊥ (ABCD), \[SA = a\sqrt 3 \]. Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc giữa CA’ và mặt (AA’B’B) bằng 30^o. Tính thể tích khối lăng trụ ABC.A’B’C’.

Cho khối lăng trụ tam giác ABC.A′B′C′có thể tích là V. Gọi I, Jlần lượt là trung điểm hai cạnh AA′và BB′. Tính thể tích của khối đa diện ABCIJC′.

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng: AD.AB = AE.AC = HC.HB.

Cho tam giác ABC có G là trọng tâm. So sánh diện tích tam giác AGB, BGC và CGA.

Chứng minh rằng: (x – y)(xⁿ – yⁿ) chia hết cho (x – y)².

Cho x, y, z, t Î ℕ^*. Chứng minh rằng:

\[M = \frac{x}{{x + y + z}} + \frac{y}{{x + y + t}} + \frac{z}{{y + z + t}} + \frac{t}{{x + z + t}}\] không phải số tự nhiên.

Gọi S là tập các giá trị của tham số m để đồ thị hàm số y = x⁴ − 2x² + m − 1có đúng một tiếp tuyến song song với trục Ox. Tìm tổng các phần tử của S.

Cho Parabol  (P): y = x² và đường thẳng (d): y = mx – m + 1.

a) Tìm toạ  độ giao điểm của (P) và (d) khi m = 4.

b) Tìm m để (d) cắt (P) tạo hai điểm phân biệt có hoành độ thoả mãn x₁ = 9x₂.

Giải phương trình sau: sin x.cos x = 1

Tính tan 45º + cot 135º.

Xác định parabol (P): y = ax² + bx + 2, biết rằng (P) đi qua hai điểm 

M (1; 5) và N (−2; 8).

Cho parabol (P): y = ax²  + bx + c có trục đối xứng là đường thẳng x = 1.  

Tính 4a + 2b.

Gieo đồng tiền cân đối và đồng chất 5 lần. Tính xác suất để được ít nhất một đồng tiền xuất hiện mặt sấp.

Tìm m để các bất phương trình \[\frac{{3\sin \,2x + \cos \,2x}}{{\sin \,2x + 4\cos {\,^2}\,x + 1}} \le m + 1\] đúng với mọi \[x \in \mathbb{R}\].

Tìm m để bất phương trình sau có nghiệm: \[{2^{{{\sin }^2}x}} + {3^{{{\cos }^2}x}} \ge m{.3^{{{\sin }^2}x}}\].

Trong không gian Oxyz cho mặt phẳng (P): x − 2y + 2z + 6 = 0 và các điểm A(−1; 2; 3), B(3; 0; −1), C(1; 4; 7). Tìm điểm M thuộc (P) sao cho MA2 + MB2 + MC² nhỏ nhất.

Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(2; 4; −1), B(1; 4; −1), C(2; 4; 3), D(2; 2; −1), biết M(x; y; z) để MA2 + MB2 + MC² + MD² đạt giá trị nhỏ nhất thì x + y + z bằng bao nhiêu?

Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Tìm các số nguyên tố p và q sao cho 7p + q và pq + 11 cũng là các số nguyên tố.

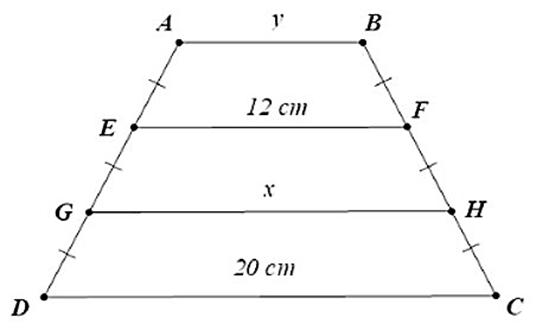
Tìm x, y trên hình vẽ, trong đó AB // EF // GH // CD.

Cho tam giác ABC có G là trọng tâm. Chứng minh diện tích tam ABC gấp 3 lần diện tích tam giác AGC.

Cho tam giác ABC có G là trọng tâm. So sánh diện tích tam giác AGB, BGC và CGA.

Một mảnh vườn hình chữ nhật có chiều dài 60 m, chiều rộng bằng \[\frac{3}{5}\] chiều dài. Tính chu vi và diện tích mảnh vườn đó.

Một mảnh vườn có chu vi là 120 m. Chiều dài hơn chiều rộng 20 m. Tính diện tích mảnh vườn.

Lớp 10B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Lý và Toán, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả Toán, Lý, Hóa. Tính số học sinh của lớp 10B.

Trong mặt phẳng Oxy cho điểm M(1;1). Tìm điểm là ảnh của M qua phép quay tâm O, góc quay 45º.

Tìm tập nghiệm của phương trình: tan x. cot x = 1.

Trong mặt phẳng tọa độ Oxy cho \[\overrightarrow v = (1; - 5)\], điểm A(2; 2), đường thẳng d: 3x + 4y − 4 = 0. Xác định đường thẳng d’ là ảnh của d qua phép tịnh tiến theo \[\overrightarrow v \].

Cho a là góc nhọn. Tính sin a biết \[\cos \,\,\alpha = \frac{2}{5}\].

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.

Sắp xếp 5 học sinh lớp A và 5 học sinh lớp B vào hai dãy ghế đối diện nhau, mỗi dãy 5 ghế sao cho 2 học sinh ngồi đối diện nhau thì khác lớp. Tìm số cách sắp xếp.

Cho hàm số y = log₂x. Khẳng định nào sau đây sai?

Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] với a > 0 có đồ thị như hình vẽ bên. Xác định dấu của b, c, d.

Cho hai tập hợp A = [– 1; 3], B = [m; m + 5]. Tìm m để A giao B khác rỗng.

Cho các tập hợp khác rỗng \[A = \left[ {m - 1;\frac{{m + 3}}{2}} \right]\] và B = (−∞;−3) ∪ [3;+∞). Tìm tập hợp các giá trị thực của m để A Ç B ¹ Æ.

Tứ giác có 2 cạnh đối song song và 2 đường chéo bằng nhau là gì?

Cho hình lập phương ABCD.A′B′C′D′có cạnh bằng 2a. Tính thể tích khối trụ ngoại tiếp hình lập phương ABCD.A′B′C′D′.

Trong dãy số \[1,\,\,2,\,\,3,\,\,4,\,\, \ldots ,\,\,199,\,\,200\] có bao nhiêu số:
a) Chia hết cho \[9\]                 

b) Chia \[9\] dư \[2\]

Cho tập hợp A = {1; 2; 3; …; 10}. Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.

Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB,CD lần lượt tai M, N. Chứng minh:    

OM = ON.

Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD lần lượt tai M, N. Chứng minh: Tứ giác BMDN là hình bình hành.

Tìm trung bình cộng của các số sau:

5; 10; 15; 20;….; 2000; 2005

Tìm 5 số chẵn liên tiếp, biết TBC của chúng bằng 126

Cho hai tập khác rỗng A = (m − 1;4 ]; B = (−2; 2m + 2), \[m \in \mathbb{R}\]. Tìm m để

A Ç B ¹Æ.

Tìm số giao điểm của đồ thị hàm số y = x⁴ − 3x² − 5 và trục hoành.

Tìm giao điểm của đồ thị hàm số y = 2x + 1 (d) và trục hoành.

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{{{(x + y)}^2}\left( {8{x^2} + 8{y^2} + 4xy - 13} \right) + 5 = 0}\\{2x + \frac{1}{{x + y}} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Giải hệ phương trình:\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = \[a\sqrt 2 \], hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC.

Cho hình vuông ABCD có AB = 7cm. Tính độ dài các đoạn thẳng BC, DC, AD

Cho khối lăng trụ tam giác ABC.A′B′C′có thể tích là V. Gọi I, Jlần lượt là trung điểm hai cạnh AA′và BB′. Tính thể tích của khối đa diện ABCIJC′.

Cho khối lăng trụ tam giác ABC.A′B′C′có thể tích là V. Tính thể tích khối chóp A.BCC’B’.

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Cho hai tập hợp A = [−2; 3] ; B = (m; m + 6). Tìm điều kiện để A ⊂ B.