7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 68)

Cho tam giác OAB vuông cân tại O, cạnh OA = a. Khẳng định nào sau đây sai?

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là

Một nhóm 9 người gồm 3 đàn ông, 4 phụ nữ và 2 đứa trẻ đi xem phim. Hỏi có bao nhiêu cách sắp xếp họ ngồi trên một hàng ghế sao cho mỗi đứa trẻ ngồi giữa hai người phụ nữ và không có hai người đàn ông nào ngồi cạnh nhau?

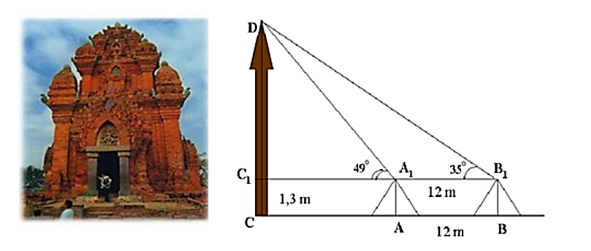
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của giác kế có chiều cao h = 1,3 m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được góc $\widehat{D{A}_1{C}_1}=49°$ và  $\widehat{D{B}_1{C}_1}=35°.$Tính chiều cao CD của tháp.

Một thầy giáo có 10 cuốn sách khác nhau trong đó có 4 cuốn sách Toán, 3 cuốn sách Lí, 3 cuốn sách Hóa. Thầy muốn lấy ra 5 cuốn và tặng cho 5 em học sinh A, B, C, D, E mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng cho các em học sinh sao cho sau khi tặng xong, mỗi một trong ba loại sách trên đều còn ít nhất một cuốn?

Cho hàm số  có đồ thị (C). Gọi d là đường thẳng đi qua A(3; 20) và có hệ số góc m. Tìm m sao cho dường thẳng d cắt (C) tại 3 điểm phân biệt.

Cho hàm số y = f(x) có bảng biến thiên như sau:

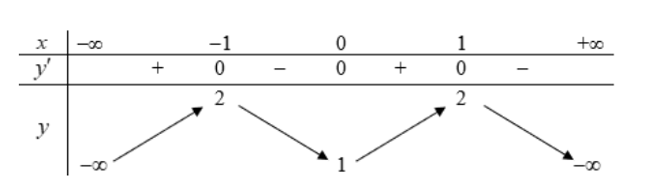
Tìm số điểm cực trị của hàm số.

Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên sau:

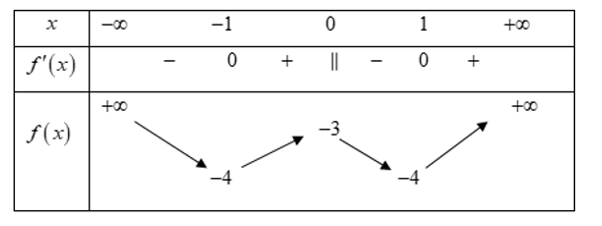
Khẳng định nào sau đây là đúng?

Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?

Gieo một đồng xu 5 lần liên tiếp. Tính số phần tử của không gian mẫu.

Trong một môn học, thầy giáo có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình và 15 câu dễ. Từ 30 câu hỏi đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu hỏi khác nhau, sao cho trong mỗi đề nhất thiết phải có đủ cả 3 câu (khó, dễ, trung bình) và số câu dễ không ít hơn 2?

Có bao nhiêu loại khối đa diện đều?

Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

Mệnh đề: "Tổng các lập phương của hai số a và b" được biểu thị bởi:

Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho?

Cho hàm số $y=a{x}^2+bx+c$  có đồ thị như dưới đây.

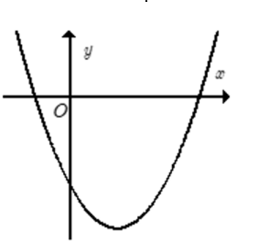
Khẳng dịnh nào sau đây đúng?

Chứng minh rằng: $\frac{1}{6}<\frac{3-\sqrt{6+\sqrt{6+\sqrt{6+\mathrm{...}+\sqrt{6+\sqrt{6}}}}}}{3-\sqrt{6+\sqrt{6+\sqrt{6+\mathrm{...}+\sqrt{6}}}}}.$

Một khối nón tròn xoay có chu vi đáy bằng 4π, độ dài đường sinh bằng 4. Tính thể tích của khối nón tròn xoay đã cho.

Cho hàm số f(x) có bảng biến thiên như sau:

Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là:

Viết phương trình tiếp tuyến d của đồ thị hàm số $y=x^3-3x^2+2$ tại điểm có hoành độ $x_0$ thỏa mãn $f^{\text{'}\text{'}}\left(x_0\right)=0.$

Một công ty Y cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có 2 loại xe, trong đó có 10 xe loại A và 9 xe loại B. Một chiếc xe loại A cho thuê với giá 4 triệu, một chiếc xe loại B cho thuê với giá 3 triệu. Biết rằng mỗi xe loại A có thể chở 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn. Công ty Y cần thuê bao nhiêu xe mỗi loại để chi phí bỏ ra ít nhất?

Cho tam giác ABC đều cạnh bằng a. Tập hợp các điểm M thỏa mãn đẳng thức $4M{A}^2+M{B}^2+M{C}^2=\frac{5a^2}{2}$ nằm trên một đường tròn (C) có bán kính R. Tính R.

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn

Cho tam giác ABC với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp, trọng tâm của tam giác. Hệ thức đúng là:

Cho hai góc nhọn α và β (α < β). Khẳng định nào sau đây là sai?

Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành.

Parabol  đạt giá trị nhỏ nhất bằng 4 tại x = -2 và đi qua A(0; 6) có phương trình là

Xác định parabol (P): y = ax² + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng $\frac{3}{4}$  khi $\frac{1}{2}$ và nhận giá trị bằng 1 khi x = 1.

Tính đạo hàm của hàm số y = cos 2x.

Cho 5 số 0, 1, 3, 6, 7. Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 3 được lập từ các số trên mà các chữ số không lặp lại?

Hỏi có bao nhiêu số có 3 chữ số chia hết cho 3 được lập từ các chữ số 1; 3; 4; 5; 7 sao cho các chữ số không lặp lại?

Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?

Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

Miền biểu diễn nghiệm của hệ bất phương trình $\left\{\begin{array}{c}y\ge -2\\ x\ge 2\\ 2x+y\le 8\end{array}\right.$ có diện tích bằng bao nhiêu?

Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ: $\left\{\begin{array}{c}x\ge -1\\ y\ge 0\\ x+y\le 4\end{array}\right..$

Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:

Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a. Tính theo a thể tích khối trụ đó.

Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các cuốn sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có mặt đối xứng nào?

Tìm mệnh đề đúng trong các mệnh đề sau:

Tìm tất cả giá trị của m để hàm số y = x³ + mx² + 4x + 3 đồng biến trên ℝ.

Hàm só nào sau đây nghịch biến trên từng khoảng xác định?

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.

a) Chứng minh tứ giác BMNC là hình thang.

b) Tứ giác MNPB là hình gì? Tại sao?

Viết phương trình đường thẳng d biết d song song với đường thẳng  y = 3x + 1 và đi qua điểm M(-2; 2).

Hình dưới đây có tất cả bao nhiêu hình vuông?

Trong mặt phẳng Oxy cho điểm M(1; 1). Hỏi trong bốn điểm được cho ở các phương án dưới đây, điểm nào là ảnh của M qua phép quay tâm O, góc $45°?$

Xét dấu tam thức f(x) = -x² – 4x + 5.

Xét dấu biểu thức f(x) = (3x2 – 10x + 3)(4x – 5).

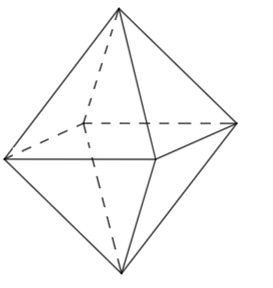
Đếm số đỉnh, số cạnh của khối bát diện đều.