7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 64)

Tìm số thực a để \(\sqrt {9 - 3a} \)có nghĩa.

Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).

Cho tam giác đều cạnh a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).

Hai đường thẳng không có điểm chung gọi là gì?

Tìm tất cả giá trị của b để hàm số y = x² + 2(b + 6)x + 4 đồng biến trong khoảng (6; +∞).

Tính nguyên hàm \(\int {\frac{{dx}}{{\cos x}}} \).

Giải phương trình: (x – 1)(x – 2)(x – 4)(x – 8) = 70x².

Cho 5 điểm A, B, C, D, E. Chứng minh

a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \overrightarrow {CB} + \overrightarrow {ED} \).

b) \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} = \overrightarrow {AE} - \overrightarrow {DB} + \overrightarrow {CB} \)

Cho hai hình bình hành ABCD và AB′C′D′ có chung đỉnh A. Khẳng định nào đúng?

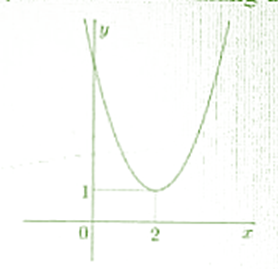
Cho hàm số bậc hai có đồ thị như hình vẽ. Hỏi hàm số đồng biến và nghịch biến trên khoảng nào?

Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, I là 3 điểm lấy trên AD, CD, SO. Xác định thiết diện của hình chóp với mặt phẳng (MNI).

Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 6a; BC = 10a; với a là số thực dương.

1) Tính BH theo a.

2) Tính cos \(\widehat {ABC}\).

Cho tam giác ABC đều, cạnh a, tâm O. Tính \(\left| {\overrightarrow {AC} - \overrightarrow {AB} - \overrightarrow {OC} } \right|\).

Cho hai số dương x;y thỏa mãn điều kiện x+y ≤ 1. Chứng minh: \({x^2} - \frac{3}{{4x}} - \frac{x}{y} \le \frac{{ - 9}}{4}\).

Chọn ngẫu nhiên 3 số từ tập S = {1; 2; ...; 11}. Tính xác suất để tổng ba số được chọn là 12.

Tính giá trị biểu thức sau : B = cos0° + cos20° + cos 40° + ... + cos160° + cos180°.

Có 6 học sinh và 2 thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai thầy giáo không đứng cạnh nhau?

Có bao nhiêu số tự nhiên có 5 chữ số khác nhau và là số chẵn?

Có bao nhiêu số tự nhiên có ba chữ số phân biệt sao cho tổng các chữ số là lẻ?

Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh đi thi. Tìm xác suất để Minh Anh được chọn đi thi.

Một tam giác có chiều cao bằng \(\frac{3}{4}\) cạnh đáy. Nếu chiều cao tăng thêm 3dm và cạnh đáy giảm đi 3dm thì diện tích của nó tăng thêm 12dm². Tính diện tích của tam giác ban đầu?

Cho phương trình (2cosx – 1)(2cos2x + 2cosx – m) = 3 – 4sin²x. Có bao nhiêu giá trị m nguyên âm lớn hơn –10 để phương trình có 2 nghiệm thuộc đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).

Tìm số thứ tư trong dãy số có 5 số chẵn liên tiếp biết tổng của năm số là 2020.

Tìm x biết: \(1 - x + \sqrt x = 2\sqrt x + 1\).

Trong mặt phẳng Oxy, cho tam giác ABC biết A (–2; –3), B (1; 1), C (3: –3). Tìm điểm M trên trục Oy sao cho \(\left| {MA - MB} \right|\) lớn nhất.

Tổng hai số bằng 37,72. Nếu số thứ nhất gấp lên 6 lần và giữ nguyên số thứ hai thì tổng hai số là 80,9. Tìm hai số ban đầu.

Xếp 6 học sinh nam và 4 học sinh nữ ngồi vào một bàn tròn 10 ghế. Tính xác suất để không có hai học sinh nữ ngồi cạnh nhau.

Viết biểu thức (x − 2y)(x² + 2xy + 4y²) dưới dạng hiệu hai lập phương.

Hỏi 962 chia 58 dư bao nhiêu, thương lấy đến 2 chữ số thập phân?

Cho hình chữ nhật ABCD tâm O, AB = 12a, AD = 5a. Tính \(\left| {\overrightarrow {AD} - \overrightarrow {AO} } \right|\).

Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tích vô hướng của hai vectơ \(\overrightarrow {BC} .\overrightarrow {CG} \)

Cho tứ diện ABCD,Gọi I J lần lượt là trung điểm của AC và BC, K là một điểm trên cạnh BD sao cho KD < KB. Tìm giao tuyến của (IJK) với (ACD) và (ABD).

Tìm 2 phân số có tử bằng 9 biết rằng giá trị của mỗi phân số đó lớn hơn \(\frac{{ - 11}}{{13}}\) và nhỏ hơn \(\frac{{ - 11}}{{15}}\).

Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1, 2, 3.

Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.

Tam giác ABC có cạnh đáy bằng gấp 3 lần chiều cao. Biết cạnh đáy hơn chiều cao 20cm. Tính diện tích của tam giác (đơn vị cm vuông).

Tìm số nguyên x để phân thức sau có giá trị nguyên \(\frac{3}{{2x - 1}}\).

Khi \(\sin A = \frac{{\cos B + \cos C}}{{\sin B + \sin C}}\) thì tam giác ABC là tam giác gì?

Chứng minh nếu m, n là số lẻ thì m² + n² chẵn.

Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M thuộc OP), IN // OP (N thuộc OQ). Chứng minh rằng: Tam giác IMN cân tại I.

Tính các góc của hình thang ABCD (AB // CD), biết rằng \[\widehat A = 3\widehat D,\widehat B - \widehat C = 30^\circ \].

Một trang trại nuôi ong mật mua 75 chiếc can loại 10 lít để đựng mật ong chuẩn bị cho vụ thu hoạch vào vụ thu hoạc số mật ong tăng gấp đôi so với dự kiến vậy để đựng hết số mật ong thu hoạch được trại nuôi ong cần mấy can 10 lít.

Cho hàm số \(y = \frac{{\sin x + 1}}{{{{\sin }^2}x + \sin x + 1}}\). M là giá trị lớn nhất, m là giá trị nhỏ nhất của y. Tính M.m?

Tính giá trị nhỏ nhất của hàm số \(y = 3x + \frac{4}{{{x^2}}}\)trên khoảng (0; +∞).

Giải phương trình: (x + 2)(x + 3) – \(2\sqrt {{x^2} + 5x + 3} = 6\).

So sánh 2²⁰⁰.2¹⁰⁰ và 3¹⁰⁰.3¹⁰⁰.

Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, AD. Tính diện tích tứ giác EFGH, biết AC = 8cm và BD = 6cm.

Cho hình vuông ABCD. Trên cạnh các AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Gọi M, N lần lượt là trung điểm của EF, BF.

a) Chứng minh các tam giác ADF và BAE bằng nhau.

b) Chứng minh MN vuông góc AF.

Cho hình thang cân ABCD có đáy lớn CD = 3, đáy nhỏ AB = 1 và AD = BC = \(\sqrt 5 \), gọi I là giao điểm của hai đường chéo hình thang, gọi H là trực tâm của tam giác BDC. Phân tích vectơ \(\overrightarrow {IH} \) theo vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} \).

Cho tam giác ABC. Đẳng thức nào sai?

Cho hai biểu thức A = \(\frac{{\sqrt x }}{{\sqrt x + 3}}\). Tính giá trị của biểu thức A khi x = 16.

Cho 3sin⁴x – cos⁴x = \(\frac{1}{2}.\) Tính A = 2sin⁴x – cos⁴x.

Cho tam giác ABC (AB = AC), trung tuyến BD. Lấy điểm E sao cho C là trung điểm AE. Gọi I là trung điểm AB. Chứng minh rằng:

a) AD = AI.

b) BE = 2CI.

c) ∆ABD = ∆ACI.

d) BE = 2BD.

Cho tam giác ABC có AB = 6cm, AC = 8cm. Gọi H là chân đường vuông góc kẻ từ B đến tia phân giác của Â, M là trung điểm của BC. Tính HM?

Cho góc α mà cosα = – 1. Tính sinα, tanα, cotα?

Giả sử M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \left( {2 + \sqrt 3 } \right)\sin x - \cos x\).

Có 4 người làm xong một công việc trong 5 ngày. Hỏi muốn làm xong công việc đó trong 4 ngày thì cần bao nhiêu người biết rằng mức làm của mỗi người là như nhau.

Trong mặt phẳng tọa độ Oxy, cho hai điểm M(0;2), N(−2;1) và vectơ \(\overrightarrow v \left( {1;2} \right)\). Phép tịnh tiến theo vectơ \(\overrightarrow v \) biến M, N thành hai điểm M’, N’ tương ứng. Tính độ dài M’N’.

So sánh 4¹⁰⁰ và 2²⁰².

Giải phương trình: x⁴ + 3x² – 4 = 0.

Cho (O, 15 cm) có nghĩa là gì?

Cho \(\frac{{1 + \cos B}}{{\sin B}} = \frac{{2a + c}}{{\sqrt {4{a^2} - {c^2}} }}\). Với a, b, c là độ dài cạnh của tam giác. Hỏi tam giác thỏa mãn đẳng thức là tam giác gì?

Tính tổng: 1² + 3² + 5² + … + (2n – 1)².

Tìm x biết: 3x + 17 = 29.

Tìm n biết: 9^{5n – 8} = 81.

Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng

\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \).

Cho a, b, c > 0 và a + b + c ≤ 1. Chứng minh rằng

\[\frac{1}{{{a^2} + 2bc}} + \frac{1}{{{b^2} + 2ac}} + \frac{1}{{{c^2} + 2ab}} \ge 9\].

Cho A = {0;1;2;3;4;5}.Từ các chữ số thuộc tập A lập được bao nhiêu số tự nhiên có 5 chữ số và số đó chia hết cho 2?

Cho tam giác ABC cân tại A, trung tuyến BD, CK. Lấy điểm E sao cho C là trung điểm của AE. Chứng minh BE = 2BD.

Cho a, b, c là các cạnh của một tam giác có diện tích S. Chứng minh rằng:

a² + b² + c² ≥ \(4\sqrt 3 S\).

Cho tam giác ABC vuông tại A, AD là phân giác. Chứng minh: \(\frac{{\sqrt 2 }}{{AD}} = \frac{1}{{AB}} + \frac{1}{{AC}}\).

Cho tổng A = 15 + 25 + x với x ∈ ℕ. Tìm x để A chia hết cho 5.

1 trường học bán trú chuẩn bị gạo đủ cho 120 học sinh trong 40 ngày sau khi ăn được một nửa thì lại có thêm số bạn học sinh nữa (số phần ăn của các học sinh không thay đổi). Hỏi nhà trường cho thêm bao nhiêu học sinh?

Tìm m để phương trình vô nghiệm mcosx – 2 = cosx + 3m.

Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho \(\widehat {BAM} = 30^\circ \).Tính tỉ số \(\frac{{MB}}{{MC}}\).

Trong mặt phẳng tọa độ Oxy,cho ΔABC  biết A(2; 4), B(5; 1), C(−1; −2). Phép tịnh tiến theo vectơ \(\overrightarrow {BC} \) biến ΔABC thành ΔA'B'C' tương ứng các điểm. Tìm tọa độ trọng tâm G’ của ΔA'B'C'.

Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm đi 84 m².

Tính bán kính đường tròn ngoại tiếp hình thang cân biết  hình thang cân ABCD (AB song song CD) có AB = 6cm; CD = 8cm và đường cao AH = 7cm.

Nêu cách xác định tâm đường tròn ngoại tiếp hình thang cân.

Tìm số tự nhiên n sao cho n² – 14n – 256 là một số chính phương.

Tìm m để hàm số \(y = \sqrt {5\sin 4x - 6\cos 4x + 2m - 1} \) xác định với mọi x.

Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến ME và MF sao cho góc EMO bằng 30 độ. Biết chu vi tam giác MEF là 30 cm. Tính:

a) Độ dài EF.

b) Diện tích tam giác MEF.

Cho khối trụ có thiết diện qua trục OO′ là một hình vuông cạnh bằng 2. Mặt phẳng (P) qua trung điểm I của OO′và tạo với mặt phẳng chứa đáy góc 30°. Diện tích của thiết diện do (P) cắt khối trụ là bao nhiêu?

Chứng minh đẳng thức: \(C_n^{k - 1} + C_n^k = C_{n + 1}^k\).

Cho hình thang cân ABCD có AC vuông góc AD. Tính chu vi và diện tích biết AB = 5cm, CD = 11cm.

Khai triển (x + 1)²⁰²⁰ có bao nhiêu số hạng?

Giải phương trình: \(8\sin x = \frac{{\sqrt 3 }}{{\cos x}} + \frac{1}{{\sin x}}\).

Tính giá trị biểu thức: A = (1 – 3m)(9m² + 3m + l) – (6 – 26m³) tại m = 5.

Giải phương trình: (cosx – sinx)sinxcosx = cosx.cos2x.

Có 4 người khách bước ngẫu nhiên vào 1 cửa hàng có 3 quầy. Tính xác suất để 3 người cùng đến quầy thứ nhất.

Tìm x biết: x² – 2x + 1 = 9.

Giải phương trình: cos2x + cosx = \(4{\sin ^2}\left( {\frac{x}{2}} \right) - 1\).

Phân tích đa thức f(x) = x⁴ – 2mx² – x + m² – m thành tích của hai tam thức bậc hai ẩn x.

Rút gọn biểu thức: \(\frac{{\sqrt x }}{x}:\frac{{ - 4}}{{\sqrt x }}\).

Tìm nghiệm dương nhỏ nhất của phương trình (2sinx – cosx)(1 + cosx) = sin²x.

Cho tam giác ABC, các cạnh BC, AC, AB có độ dài lần lượt là a, b, c. Chứng minh rằng: \(\frac{{\cos A + \cos B}}{{a + b}} = \frac{{\left( {b + c - a} \right)\left( {c + a - b} \right)}}{{2abc}}\).

So sánh 17 yến và 170kg.

Tìm x biết: \(\frac{{2x - 3}}{3} - \frac{3}{2} = \frac{{5 - 3x}}{6} - \frac{1}{3}\).

Rút gọn biểu thức: \(A = \left( {\frac{{2x + 1}}{{x\sqrt x - 1}} - \frac{{\sqrt x }}{{x + \sqrt x + 1}}} \right).\left( {\frac{{1 + x\sqrt x }}{{1 + \sqrt x }} - \sqrt x } \right)\) với x ≥ 0; x ≠ 1.

Tìm x biết: (8 – 5x)(x + 2) + 4(x – 2)(x + 1) + 2(x – 2)(x + 2) = 0.

Tính B = (a – b)(a⁴ + a³b + a²b² + ab³ + b⁴).

Số 0.5 và –0.5 có phải số nguyên không?

Tính giá trị biểu thức: \({4.2^3}:\left[ {{2^7}.{{\left( {\frac{1}{3}} \right)}^2}} \right]\).

Cho tam giác ABC vuông tại A và đường cao AH. Biết AB = 15cm, AC = 20cm.

a) Tính BC.

b) Tính AH, BH và HC.

Giải phương trình: \(\sqrt 3 \cos x - \sin x = \sqrt 3 \).

Với A, B, C là 3 góc trong 1 tam giác, chứng minh

sin A + sin B + sin C = \(4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}\).

Tìm các hệ số a,b,c sao cho đa thức 3x⁴ + ax² + bx + c chia hết cho đa thức (x – 2) và chia cho đa thức (x² – 1) được thương và còn dư (–7x – 1).

Tính giá trị biểu thức: (–63) – (–17).

Cho mệnh đề “∀m ∈ ℝ, x² – 2x – m² = 0 có nghiệm”. Phủ định mệnh đề này là?

So sánh 302mm² và 3dm²2mm².

So sánh 32km²45m² và 3200hm².

Cho A=2+2²+2³+...+2²⁰. Chứng minh rằng:

a) A chia hết cho 2;

b) A chia hết cho 3;

c) A chia hết cho 5.

Tìm các số nguyên x biết: (8x – 1)^{2x + 1} = 5^{2x + 1}.

Tính giá trị: 36.4 – 4(82 – 7.11)² : 4 – 2016⁰.

Một xe bus chạy đều trên quãng đường AB dài 120km mất 1 khoảng thời gian nhất định. Một lần sau khi khởi hành từ A được 60p thì xe bị ngăn lại 10 phút để nhường đường cho 1 đoàn xe công vụ. Để đi tiếp đến B theo đúng dự định thì xe buýt phải tăng vận tốc thêm 6km/h. Tính vận tốc ban đầu của xe?

Có 10 người ngồi xung quanh bàn tròn, mỗi người cầm một đồng xu như nhau. Tất cả 10 người cùng tung đồng xu của họ, người có đồng xu ngửa thì đứng, người có đồng xu úp thì ngồi. Tính xác suất để có đúng 4 người cùng đứng, trong đó có đúng hai người đứng liền kề?

Nghiệm kép là gì?

Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Tích hai số thực trái dấu là một số thực âm.

b) Mọi số tự nhiên đều là dương.

c) Có sự sống ngoài Trái Đất

d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.

Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng Em cắt tia By tại F.

a) Chứng minh EF là tiếp tuyến của đường tròn (O).

b) Chứng minh tam giác EOF là tam giác vuông.

c) Chứng minh AM.OE + BM.OF = AB.EF.

Cho tam giác MNP vuông tại M đường cao MH. Gọi D, F lần lượt là chân các đường vuông góc HA từ H xuống MN và MP.

a) Chứng minh tứ giác MDHE là Hình chữ nhật.

b) Gọi A là trung điểm HP. Chứng minh ∆DEA là tam giác vuông.

c) Tam giác MNP có thêm điều kiện gì để DE = 2EA.

Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là 300 ca – lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca – lo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ hai cung cấp 60 ca – lo, 6 đơn vị vitamin A và 30 đơn vị vitamin C.

a) Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.

b) Chỉ ra hai phương án mà bác Ngọc có thể chọn lựa số lượng cốc cho đồ uống thứ nhất và thứ hai nhằm đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.

Số các ước tự nhiên của 252 là bao nhiêu? Liệt kê các ước của 252.

Tháng 11 vừa qua, có ngày Black Friday phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mau một đôi giày. Biết đôi giày đang khuyến mãi giảm giá 40%, mẹ An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa, do đó mẹ An chỉ phải trả 684.000 cho đôi giày. Hỏi giá bán ban đầu của đôi giày nếu không khuyến mãi là bao nhiêu?

Dưới đây là phép nhân sai, hãy tìm phép nhân đúng?

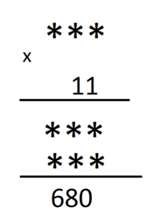
Bạn thứ nhất có 1 con súc sắc, bạn thứ 2 có 1 đồng tiền(đều cân đối đồng chất). Xét phép thử : “Bạn thứ nhất gieo con súc sắc, sau đó bạn thứ hai gieo đồng tiền”.

a) Hãy mô tả không gian mẫu.

b) Xác định biến cố A: “Con súc sắc xuất hiện mặt 4 chấm”. Tính P(A).

Giả sử ta dùng thước và compa vẽ hình thoi ABCD, biết AB = 5cm và AC = 8cm.

Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.

a) Tính thể tích của hồ bơi.

b) Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).

c) Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.

Biểu diễn các góc lượng giác trên đường tròn lượng giác: \(k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

So sánh 0,0125 và 0,005.

Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm đi 84 m².

Cho ngũ giác đều ABCDE tâm O. Phép quay nào sau đây biến ngũ giác thành chính nó?

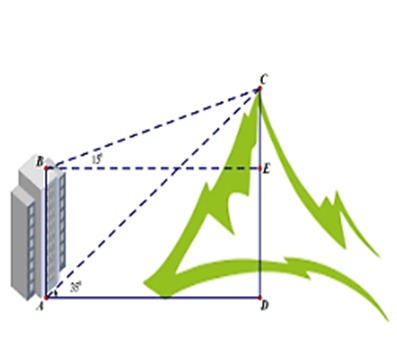
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 60 m.

Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?

Để kích cầu tiêu dùng sau mùa dịch Covid –19 lần thứ 4, một cửa hàng giày có chương trình khuyến mãi như sau:

1. Giảm giá 30% so với giá niêm yết cho tất cả sản phẩm của cửa hàng.

2. Nếu khách hàng có thể thành viên của của hàng thì được giảm thêm 20% so với giá đã giảm. Bình có thể thành viên của cửa hàng trên và mua một đôi giày có giá niêm yết là 2 triệu đồng.

Hỏi Bình phải trả cho cửa hàng bao nhiêu tiền?

Bạn An viết một trang web để kết bạn. Trang web đã nhận được 3 lượt truy cập trong tuần đầu tiên. Nếu số lượt truy cập tuần tiếp theo gấp 3 lần số lượt truy cập tuần trước thì sau 6 tuần đầu tiên, trang web của bạn Na có tất cả bao nhiêu lượt truy cập?