7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 61)

Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn:  $2\overrightarrow{MA}+3\overrightarrow{MB}=\overrightarrow{0}$ được xác định bởi:

Cho hai điểm A, B phân biệt. Xác định điểm M biết  $2\overrightarrow{MA}-3\overrightarrow{MB}=\overrightarrow{0}$.

Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: $\frac{a}{b+c-a}+\frac{b}{a+c-b}+\frac{c}{a+b-c}\ge 3$.

Cho a, b, c là độ dài 3 cạnh tam giác. Chứng minh rằng:

$\frac{ab}{a+b-c}+\frac{bc}{b+c-a}+\frac{ca}{c+a-b}\ge a+b+c$.

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có A(5; 2), phương trình đường trung trực cạnh BC, đường trung tuyến CC' lần lượt là d: x + y − 6 = 0 và d': 2x − y + 3 = 0. Tìm tọa độ các đỉnh còn lại của ∆ABC.

Trong mặt phẳng tọa độ Oxy cho tam giác ABC có  $M\left(-\frac{5}{2};-1\right),N\left(-\frac{3}{2};-\frac{7}{2}\right),P\left(0;\frac{1}{2}\right)$ lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm tọa độ trọng tâm G của tam giác ABC.

Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Tìm thiết diện của mặt phẳng (P) và tứ diện ABCD.

Cho hình tứ diện ABCD. Gọi I, J lần lượt thuộc cạnh AD, BC sao cho IA = 2ID, JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Khẳng định nào đúng?

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC.

Một hộp đựng tám thẻ được ghi từ 1 đến 8. Lấy ngẫu nhiên từ hộp đó ba thẻ, tính xác suất để tổng các số ghi trên ba thẻ đó bằng 11.

Một hộp đựng 8 viên bi đỏ được đánh số từ 1 đến 8, 6 viên bi xanh được đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn 2 viên bi từ hộp đó sao cho 2 viên bi khác màu và khác số.

Đồ thị hàm số y = x³ − 4x + 3 cắt trục hoành tại điểm có hoành độ là bao nhiêu?

Đồ thị hàm số y = x⁴ − x³ − 2 cắt trục hoành tại bao nhiêu điểm?

Nghiệm của phương trình log₃ (2x − 1) = 2 là:

Tìm tập nghiệm S của phương trình log₃ (2x + 1) − log₃ (x − 1) = 1

Tìm tập xác định D của hàm số y = log₂ (x³ − 8)¹⁰⁰⁰

Tập nghiệm của bất phương trình  $9^{{\log }_9^{2}x}+x^{{\log }_{9}x}\le 18$ là:

Cho hai số phức z₁, z₂ thỏa mãn |z₁| = |z₂| = |z₁ − z₂| = 1. Tính giá trị của biểu thức  $P={\left(\frac{z_1}{z_2}\right)}^2+{\left(\frac{z_2}{z_1}\right)}^2$.

Cho hai số phức z₁, z₂ thỏa mãn các điều kiện |z₁| = |z₂| = 2 và |z₁ + 2z₂| = 4. Tính giá trị của |2z₁ − z₂|.

Cho hàm số f (x) = x²ln x. Tính f ¢(e).

F (x) là một nguyên hàm của hàm số f (x) = ln x và F (1) = 3. Khi đó giá trị của F (e) là:

Cho hàm số  $y=\ln \frac{7}{x+7}$. Hệ thức nào sau đây là hệ thức đúng?

Giải phương trình ln (7x) = 7.

Cho hàm số  $y=\frac{5x+9}{x-1}$. Khẳng định nào sau đây là đúng?

Cho hàm số y = f (x) thỏa mãn f ¢(x) = x² − 5x + 4. Khẳng định nào sau đây là đúng?

Cho hình lập phương ABCD.A'B'C'D'. Hỏi góc giữa hai đường thẳng BA' và CD bằng bao nhiêu?

Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BA' và B'D' bằng bao nhiêu?

Cho số phức z thỏa mãn |z + i + 1| = |z − 2i|. Tìm giá trị nhỏ nhất của modun của số phức z.

Cho số phức z thỏa mãn  $\left|z+i+1\right|=\left|\overline{z}-2i\right|$. Tìm giá trị nhỏ nhất của |z|.

Cho số phức z thỏa mãn |z − 4 − i| = |z + i|. Gọi z = a + bi (a; b Îℝ) là số phức thỏa mãn |z − 1 + 3i| nhỏ nhất. Giá trị của biểu thức T = 2a + 3b là:

Cho các số phức z thỏa mãn |z − 2i| = |z + 2|. Gọi z là số phức thỏa mãn |(2 − i)z + 5| nhỏ nhất. Khi đó:

Hàm số y = cos 2x nghịch biến trên khoảng nào?

Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm A(4; 0), B(1; 4) và C(1; −1). Gọi G là trọng tâm tam giác ABC. Biết rằng G là điểm biểu diễn số phức z. Mệnh dề nào sau đây là đúng?

Trong mặt phẳng Oxy cho tam giác ABC với A(1; 3), B(2; −4), C(3; −2) và điểm G và trọng tâm tam giác ABC. Ảnh G' của G qua phép đối xứng trục Ox có tọa độ là:

Tìm tất cả các giá trị của tham số m để hàm số y =−x³ + 2x² − mx + 1 đạt cực tiểu tại x = 1.

Tìm m để hàm số y = x³ − 2mx² + mx + 1 đạt cực tiểu tại x = 1.

Đội thanh niên xung kích có của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?

Hình nào sau đây không có tâm đối xứng?

Hình nào sau đây không có tâm đối xứng?

Một hình trụ có đường kính đáy bằng chiều cao nội tiếp trong mặt cầu bán kính R. Diện tích xung quanh của hình trụ bằng:

Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là:

Giải phương trình:  $1+\sin x+\cos x=2\cos \left(\frac{x}{2}-\frac{\pi }{4}\right)$.

Giải phương trình:  $\frac{1}{\cos x}-\frac{1}{\sin x}=2\sqrt{2}\cos \left(x+\frac{\pi }{4}\right)$.

Biến đổi $\underset{0}{\overset{3}{\int }}\frac{x}{1+\sqrt{1+x}}dx$ thành  $\underset{1}{\overset{2}{\int }}f\left(t\right)dt$, với  $t=\sqrt{1+x}$. Khi đó f (t) là hàm số nào trong các hàm số sau đây?

Tính nguyên hàm của hàm số f (x) = (3x + 2)³.

Tính nguyên hàm  $\int \frac{dx}{2\tan x+1}$.

Cho hàm số f(x) liên tục trên ℝ và thỏa mãn  $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\tan x.f\left({\cos }^{2}x\right)dx=2$ và  $\underset{e}{\overset{e^2}{\int }}\frac{f\left({\ln }^{2}x\right)}{x.\ln x}dx=2$. Tính  $\underset{\frac{1}{4}}{\overset{2}{\int }}\frac{f\left(2x\right)}{x}dx$.

Tính giá trị của biểu thức:

$P=C_{2017}^0{C}_{2018}^1+C_{2017}^1{C}_{2018}^2+\mathrm{...}+C_{2017}^{2016}{C}_{2018}^{2017}+C_{2017}^{2017}{C}_{2018}^{2018}$.

Tính tổng:  $S=1.C_{2018}^1+2.C_{2018}^2+\mathrm{...}+2018.C_{2018}^{2018}$.

Trong mặt phẳng tọa độ Oxy cho 4 điểm A(2; 5); B(1; 7); C(1; 5); D(0; 9). Ba điểm nào sau đây thẳng hàng.

Cho 4 điểm A(1; −2); B(0; 3); C(−3; 4); D(−1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?

Cho  $\overrightarrow{AB}\ne \overrightarrow{0}$ và một điểm C. Có bao nhiêu điểm D thỏa mãn  $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|$?

Cho  $\overrightarrow{AB}$ và một điểm C. Có bao nhiêu điểm D thỏa mãn  $\overrightarrow{AB}=\overrightarrow{CD}$?

Cho số phức z thỏa mãn |z| = 4. Biết tập hợp biểu diễn các số phức w = (3 + 4i)z + i là một đường tròn. Tìm bán kính Rcủa đường tròn đó.

Cho số phức z thỏa mãn |z| = 2. Biết rằng tập hợp các điểm biểu diễn của số phức w = 3 − 2i + (2 − i)z là một đường tròn, bán kính Rcủa đường tròn đó bằng:

Cho hàm số f (x) liên tục trên ℝ và thoả mãn 

$f\left(x\right)+f\left(-x\right)=\sqrt{2+2\cos 2x},\forall x\in ℝ$. Tính  $I=\underset{-\frac{3\pi }{2}}{\overset{\frac{3\pi }{2}}{\int }}f\left(x\right)dx$.

Cho hàm số f (x) liên tục trên ℝ và thoả mãn f (x) + f (−x) = 2cos 2x, "x Î ℝ. Khi đó  $I=\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}f\left(x\right)dx$ bằng:

Cho hàm số f (x) liên tục trên ℝ. Biết rằng  $\underset{0}{\overset{\ln 2}{\int }}f\left(e^x+1\right)dx=5$ và  $\underset{2}{\overset{3}{\int }}\frac{\left(2x-3\right)f\left(x\right)}{x-1}dx=3$. Tính  $I=\underset{2}{\overset{3}{\int }}f\left(x\right)dx$.

Cho hàm số f (x) liên tục trên ℝ và có  $\underset{0}{\overset{2}{\int }}f\left(x\right)dx=3$. Tính  $\underset{-1}{\overset{1}{\int }}f\left(\left|2x\right|\right)dx$.

Cho hàm số f (x) = x²ln x. Tính f ¢(e).

Biết hàm số F (x) là một nguyên hàm của hàm số  $f\left(x\right)=\frac{\ln x}{x\sqrt{{\ln }^{2}x+3}}$ có đồ thị đi qua điểm (e; 2016). Khi đó hàm số F (1) là:

Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây là đúng?

Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?

Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình

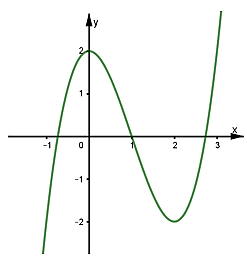
Gọi m là số nghiệm của phương trình f(f(x))= 1. Khẳng định nào sau đây là đúng?

Cho hàm số y = f (x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình f (x + 2019) = 1 là:

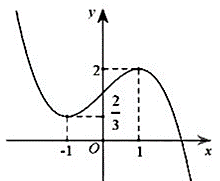
Cho hàm số f (x) liên tục trên ℝ và thoả mãn f (x) + f (−x) = 3 − 2cos x, với mọi x Î ℝ. Tính tích phân  $I=\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}f\left(x\right)dx$?

Cho hàm số f (x) liên tục trên ℝ và thoả mãn 

 $f\left(x\right)+f\left(-x\right)=\sqrt{2+2\cos 2x},\forall x\in ℝ$. Tính  $I=\underset{-\frac{3\pi }{2}}{\overset{\frac{3\pi }{2}}{\int }}f\left(x\right)dx$.

Cho hàm số f (x) liên tục trên ℝ và  $\underset{0}{\overset{1}{\int }}f\left(2x\right)dx=8$. Tính  $I=\underset{0}{\overset{\sqrt{2}}{\int }}x.f\left(x^2\right)dx$.

Cho f (x) liên tục trên ℝ và f (2) = 16,  $\underset{0}{\overset{1}{\int }}f\left(2x\right)dx=2$. Tích phân  $\underset{0}{\overset{2}{\int }}x{f}^{\text{'}}\left(x\right)dx$  bằng:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng đáy trùng với trọng tâm tam giác ABD.Cạnh bên SD tạo với đáy một góc 60°. Tính thể tích khối chóp S.ABCD.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng A B C D trùng với trọng tâm G của tam giác ABD. Đường thẳng SD tạo với mặt phẳng một góc 60°. Tính khoảng cách giữa hai đường thẳng AB và SC.

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và  $SA=\sqrt{2}a$. Tính thể tích V của khối chóp S.ABCD.

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và  $SA=a\sqrt{6}$. Tính thể tích của khối chóp S.ABCD.

Hình trụ có bán kính đáy bằng a và thiết diện qua trục là một hình vuông. Tính thể tích khối trụ đó.

Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính theo a diện tích xung quanh của hình trụ.

Cho hai số thực x, y thay đổi thỏa mãn điều kiện x² + y² = 2. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2(x³ + y³) − 3xy. Tính giá trị của M + m.

Cho x, y là những số thực thoả mãn x² − xy + y² = 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của  $P=\frac{x^4+y^4+1}{x^2+y^2+1}$.

Tính giá trị của A = M + 15m.

Cho x > 0, y > 0 thỏa mãn xy = 6. Tìm giá trị nhỏ nhất của biểu thức:

 $Q=\frac{2}{x}+\frac{3}{y}+\frac{6}{3x+2y}$.

Cho x > 0, y > 0 thỏa mãn x + y ≥ 6. Tính GTNN của biểu thức: $M=3x+2y+\frac{6}{x}+\frac{8}{y}$.

Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho  $AM=\frac{1}{5}AB$. Tìm k trong  $\overrightarrow{MA}=k\overrightarrow{MB}$.

Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho  $AM=\frac{1}{5}AB$. Tính giá trị của k để có đẳng thức  $\overrightarrow{AM}=k.\overrightarrow{AB}$.

Cho f (x) là hàm số chẵn, liên tục trên đoạn [−1; 1] và  $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=4$. Kết quả $I=\underset{-1}{\overset{1}{\int }}\frac{f\left(x\right)}{1+e^x}dx$ bằng bao nhiêu?

Cho hàm số y = f (x) là hàm số chẵn, liên tục trên đoạn [−1; 1] và thỏa mãn  $\underset{0}{\overset{\frac{1}{2}}{\int }}f\left(x\right)dx=3;\underset{\frac{1}{4}}{\overset{\frac{1}{2}}{\int }}f\left(2x\right)dx=10$. Tính  $I=\underset{-\frac{\pi }{2}}{\overset{0}{\int }}\cos xf\left(\sin x\right)dx$.

Có bao nhiêu số tự nhiên chia hết cho 5 mà mỗi số có bốn chữ số khác nhau?

Có bao nhiêu số tự nhiên có 4 chữ số chia hết cho 5?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số  $y=\sin x+\sqrt{3}\cos x+1$ lần lượt là M, m. Tính tổng M + m.

Tìm giá trị lớn nhất của hàm số  $y=\sin x-\sqrt{3}\cos x$