7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 60)

Giải phương trình: sin2x – cos2x + 3sinx – cosx – 1 = 0.

Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.

Làm theo mẫu: \(\frac{{143}}{{10}} = 14;\frac{3}{{10}} = 0,3\).

Yêu cầu: \(\frac{{126}}{{100}} = ...;\frac{{26}}{{100}} = ...\)

\(\frac{{1246}}{{10}} = ...;\frac{6}{{10}} = ...\)

Tích các nghiệm của phương trình: log_x(125x) . log₂₅²x = 1?

Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đố với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?

Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OC = 2cm. Tính AC ?

Cho sinx + cosx = m. Tính theo m giá trị của M = sinxcosx.

Phân tích thành nhân tử: \(x\sqrt x - 1 + \sqrt x - x\).

Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thể làm 40 giờ/tuần và tốn 6h làm 1 cái bàn, 3h làm 1 cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp 3 lần số bàn. Một cái bàn chiếm chỗ bằng 3 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Hỏi người thợ mộc phải sản xuất như nào để có tiền lãi thu về là lớn nhất.

Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM = 15, BN = 12 và tam giác CMN có diện tích là \(15\sqrt 3 \). Tính độ dài đoạn thẳng MN.

Nếu x² + 1 ≠ 0 thì x ≠ – 1, đúng hay sai?

Cho x + 2y = 5. Tính giá trị biểu thức A = x² + 4y² – 2x + 10 + 4xy – 4y.

Phủ định của mệnh đề “∃x ∈ ℝ, x² – x + 1 < 0” là mệnh đề nào?

Cho tập hợp A = {x ∈ ℝ| x – a| ≤ 2} và B = (– 2; 5]. Biết rằng tập hợp tất cả các giá trị a để A giao B khác rỗng là nửa khoảng (m; n]. Tính S = n + 2m.

Từ điểm A ở ngoài đường tròn (O; R), kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B và vuông góc với OA tại H cắt (O) tại C. Vẽ đường kính BD của (O).

a) Chứng minh: AC là tiếp tuyến của (O).

b) Chứng minh: DC.OA = 2R² .

Nhân ngày 20/10, một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiết của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy thu ngân.

a) Chị Hoa không có thẻ thân thiết của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1.050.000đ. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?

b) Cô Hà có thẻ khách hàng thân thiết, cô mua một chiếc túi xách và nhận được một voucher trị giá 91.000đ. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?

Tính giá trị biểu thức: – 87 + (–12) – (–487) + 512

Tìm đạo hàm của hàm số \(y = \frac{{x - 1}}{{\sqrt {{x^2} + 1} }}\).

Trong một kì kiểm tra, có 42% học sinh không đạt môn nhảy xa, 52% không đạt môn đá cầu, trong đó 17% học sinh không đạt cả 2 môn, hãy tính % số học sinh đã đạt cả hai môn đó.

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I.
a. Chứng minh: AD//BM và tứ giác ADBM là hình thoi.
b. Gọi E là giao điểm AM và DC. Chứng minh: AE = EM.

Hình chữ “H” có bao nhiêu trục đối xứng?

Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy, SA = \(a\sqrt 6 \). Tính góc giữa SC và (SAB).

Tổng các nghiệm thuộc khoảng (0;2018) của phương trình: \({\sin ^4}\frac{x}{2} + {\cos ^4}\frac{x}{2} = 1 - 2\sin x\) là?

Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:

P = x² + 5y² + 4xy + 6x + 16y + 32.

Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, biết AB = AC = AD = 1. Số đo góc giữa hai đường thẳng AB và CD bằng?

Có bao nhiêu cách sắp ngẫu nhiên 10 học sinh gồm 2 học sinh 11A, 3 học sinh lớp 11B và 5 học sinh lớp 11C thành 1 hàng ngang sao cho không có học sinh nào cùng lớp đứng cạnh?

Tìm số hạng thứ 7 trong khai triển (x + 2)¹⁰.

Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).

Phân tích đa thức thành nhân tử: –x² – 2xy – y².

Biết 48 lít dầu nặng 36 kg. Một can chứa dầu nặng 30 kg. Biết cân nặng của can khi rỗng là 1,5 kg, số lít dầu chứa trong can đó là?

Lớp 6A có 42 học sinh, lớp 6B có 54 học sinh và lớp 6C có 48 học sinh. Cô phụ trách đã xếp đều số học sinh của 3 lớp thành một số hàng như nhau. Tính số hàng nhiều nhất có thể xếp được.

Tìm y biết: 76,22 – y . 3 = 30,61 . 2.

Với x là số tự nhiên lớn hơn 3, tìm giá trị lớn nhất của P = \(\frac{{2\sqrt x + 6}}{{\sqrt x + 2}}\).

Tìm x biết: x(x – 4) = 0.

Tính giá trị biểu thức x + (–10) biết x = –28

Một thửa ruộng hình chữ nhật có chu vi là 96 m, chiều dài bằng \(\frac{5}{3}\) chiều rộng, người ta lấy \(\frac{1}{2}\) diện tích ăn quả. Tính diện tích ăn quả?

Đúng ghi Đ sai ghi S:

a) 418 cm = 41,8 m.

b) 53 cm = 0,53 m.

c)105 cm = 1,05 m.

d) 908 dm = 9,08 m.

Đặt tính rồi tính: 199,2 : 24.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD, OC.

a) Tìm Tìm giao tuyến của mặt phẳng (MNP) với mp (SAC).

b) Tìm giao điểm của SA với mp (MNP).

c) Tìm thiết diện của S.ABCD với (AMN).

Cho đường tròn đường kính AB vẽ tiếp tuyến Ax , By từ M trên đường tròn M khác A, B vẽ tiếp tuyến thứ 3 nó cắt Ax tại C cắt By tại D gọi N là giao điểm của BC và AO.

a) Chứng minh: \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\).

b) Chứng minh: MN vuông góc AB.

c) Chứng minh: \(\widehat {COD} = 90^\circ \).

Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.

x – y và y – x có giống nhau không? Vì sao?

Đặt tính rồi tính: 112,56 : 28.

Số dư của phép chia 37,99 : 16 nếu lấy đến 2 chữ số ở phần thập phân của thương là bao nhiêu?

A, B và C chạy quanh một đường tròn có chiều dài 750m với tốc độ lần lượt là 3 m/giây, 6m/giây và 18m/giây. Nếu cả ba bắt đầu từ cùng một điểm, đồng thời và chạy theo cùng một hướng, khi nào họ sẽ gặp nhau lần đầu tiên sau khi họ bắt đầu cuộc đua?

Cho hình vuông ABCD tâm O, cạnh bằng a. Tính \(\left| {\overrightarrow {AC} } \right|\).

Cho tam giác ABC có \(\widehat A = 90^\circ \), trên cạnh BC lấy điểm E sao cho BA = BE. Tia phân giác góc B cắt AC ở D.

a) So sánh DA và DE.

b) Tính số đo \(\widehat {BED}\).

Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG.

a) Chứng minh tứ giác BCGE là hình thang cân.

b) Gọi K là giao điểm của các tia DE và FG, M là trung điểm của đoạn thẳng EG. Chứng minh ba điểm K, A, M thẳng hàng.

c) Chứng minh \(\widehat {COD} = 90^\circ \). 

d) Chứng minh DC, FB và AM đồng quy.

Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E. Gọi M, N, P, Q lần lượt là trung điểm của DE, EB, BC, CD. Chứng minh: 4 điểm M, N, P, Q cùng thuộc 1 đường tròn.

Cho tam giác nhọn ABC có AD là phân giác trong góc A (D thuộc BC) . Đường thẳng qua d song song với AB cắt AC tại I , đường thẳng qua d song song AC cắt AB tại K. Chứng minh rằng tam giác IDK là tam giác cân.

Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (O) với A, B là các tiếp điểm. Chứng minh 4 điểm A, B, O, M cùng thuộc một đường tròn.

Hình thoi ABCD có diện tích 20 cm² và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.

Cho điểm M nằm ngoài đường tròn (O;R). Từ M kẻ các tiếp tuyến MA, MB tới đường tròn tâm O (A, B là các tiếp điểm). Gọi H là giao điểm của MO với AB. Kẻ đường kính AD của đường tròn (O), MD cắt đường tròn (O) tại điểm thứ hai là C. Chứng minh rằng \(\widehat {MHC} = \widehat {ADC}\).

Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?

Một ô tô cứ đi 100km thì tiêu thụ hết 12,5 lít xăng. Hỏi ô tô đó đi quãng đường dài 60km thì tiêu thụ hết bao nhiêu xăng ?

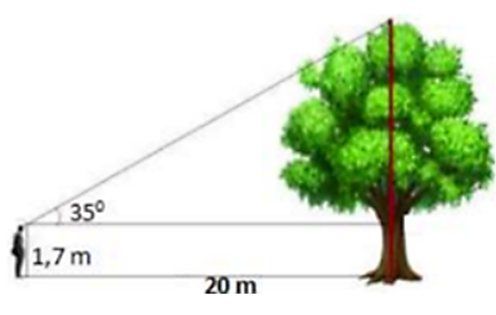
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất).

Tìm x để y = sinx + cosx + sin2x – 1 đạt giá trị lớn nhất.

Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:

y =\(\frac{{ - 1}}{2}x\) (d₁) và y = \(\frac{1}{2}x\) + 3 (d₂).

Xác định b để đường thẳng (d₃) y = 2x + b cắt (d₂) tại điểm có tung độ và hoành độ đối nhau.

Tìm n biết: (n – 3) + (n – 2) + (n – 1) + .... + 10 + 11 = 11.

Tính bằng cách thuận tiện: \(\frac{1}{{10.11}} + \frac{1}{{11.12}} + ... + \frac{1}{{49.50}}\).

Trong phép tính 121,23:14 và có thương là 8,65. Vậy số dư là bao nhiêu?

Đặt tính rồi tính: 173,44 : 32.

Cho tam giác ABC. M, N là trung điểm AB, AC. Chứng minh: \(\overrightarrow {AB} = \frac{{ - 2}}{3}\overrightarrow {CM} - \frac{4}{3}\overrightarrow {BN} \).

2 giờ và 45 phút tương đương với 2,75 giờ. Đúng hay sai?

Tính: 99 + (–5) + (–104) + 11.

Tính nhanh: [(–59) + 71] – [–83 – (–95)].

Cho a = –13; b = 25; c = –30. Tính giá trị biểu thức:

a) a + a + 12 – b.

b) a + b – (c + b).

c) 25 + a – (b + c) – a.

Tìm giá trị n ∈ ℕ thỏa mãn \(C_{n + 1}^1 + 3C_{n + 2}^2 = C_{n + 1}^3\).

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Cho hình thang vuông ABCD (\(\widehat A\) = \(\widehat D\)= 90°) có \[\widehat {BMC}\]= 90°, với M là trung điểm của AD. Chứng minh: AD là tiếp tuyến của đường tròn bán kính BC.

 Cho hình vuông có chu vi 20cm. Nếu kéo dài mỗi cạnh của hình vuông thêm 3cm thì hình vuông mới có chu vi là bao nhiêu ?

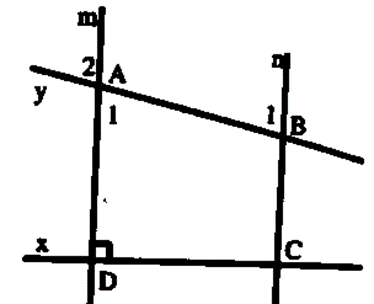
Cho hình vẽ sau, biết m // n và x ⊥ m.

1) Chứng minh: x ⊥ n.

2) Tính các góc \(\widehat {{A_1}},\widehat {{A_2}}\) biết \(\widehat {{B_1}} = 60^\circ \).

Cho lục giác ABCDEF. Có bao nhiêu vectơ khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối là hai đỉnh của lục giác.

Cho một số tự nhiên gồm các số tự nhiên liên tiếp từ 1 đến 2020, được viết theo thứ tự liền nhau như sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 … 2017 2018 2019 2020 2021. Hãy tính tổng tất cả các chữ số của số đó?

Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.

1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.

2) Chứng minh: BH.BA = BK.BC.

3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.

Cho tam giác ABC có AB = a, AC = 2a. Gọi D là trung điểm AC, M là điểm thỏa mãn \[\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \]. Chứng minh: BD vuông góc AM.

Cho tam giác ABC vuông tại A (AB < AC) có D và E lần lượt là trung điểm của các cạnh AC và BC. Vẽ EF vuông góc với AB tại F.

a) Chứng minh rằng DE //AB và tứ giác ADEF là hình chữ nhật.

b) Trên tia đối của tia DE lấy điểm G sao cho DG = DE. Chứng minh tứ giác AECG là hình thoi.

c) Gọi O là giao điểm của AE và DF. Chứng minh rằng ba điểm B, O, G thẳng hàng.

d) Vẽ EH vuông góc với AG tại H. Chứng minh rằng tam giác DHF vuông.

Cho tam giác ABC vuông tại A có \(\widehat C = 30^\circ \). Gọi M và N lần lượt là trung điểm của BC và AC.

a) Tính \(\widehat {NMC}\).

b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác AECM là hình thoi.

c)Lấy D là điểm đối xứng với E qua BC. Tứ giác ACDB là hình gì? Tại sao?

d) Tam giác ABC có điều kiện gì thì tứ giác AECM là hình vuông?

Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB và AC. Tứ giác ADME là hình gì?

Cho tứ diện ABCD có AB = AC = AD = 24, BC = CD = DB = 15. Trên cạnh AB lấy điểm P sao cho PA = x.PB. Với giá trị nào của x thì mặt phẳng (a) qua P song song với AC và BD cắt tứ diện ABCD theo thiết diện là một hình thoi?

Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.

a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.

b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R². Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6cm.

Cho (d₁): y = (2m + 1)x – 2m – 3 và d₂: y = (m – 1)x + m. Tìm m để d₁ và d₂ cắt nhau tại 1 điểm nằm trên trục hoành.

Biết đồ thị hàm số y = (k – 3)x – 4 cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5. Tìm tham số k?

Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB). Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.

a) Chứng minh K là trung điểm của AB.

b) Vẽ MH ⊥ OI tại H. Chứng minh OB² = OH.OI.

c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.

Hình chữ nhật có chiều dài và chiều rộng cùng tăng 4 lần thì diện tích của nó tăng lên bao nhiêu lần?

Chứng minh không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \sin x\).

Lớp 11A1 có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ?

Một hình bình hành ABCD có diện tích 350 cm², biết độ dài đường cao AH = 35 cm. Tính độ dài cạnh AB.

Một xe khởi hành từ địa điểm A lúc 8 giờ sáng đi tới điểm B cách A 115 km, chuyển động thẳng đều với tốc độ 40 km/h. Một xe khác khởi hành từ B lúc 8 giờ 30 phút sáng đi về A, chuyển động thẳng đều với tốc độ 50 km/h. Xác định thời điểm hai xe gặp nhau.

Đặt tính rồi tính: 199,2 : 24.

Vẽ đồ thị hàm số y = (m – 1)x + 2m – 5 khi m = 1.5 Tính góc tạo bởi đường thẳng vẽ được và trục hoành ( kết quả làm tròn đến phút).

Tính giá trị biểu thức: (–167) . (67 – 34).

Bỏ ngoặc rồi tính: (123 – 27) + (27 + 13 – 123).

Cho 2 vectơ \(\overrightarrow a ,\overrightarrow b \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4;\left| {\overrightarrow b } \right| = 3;\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi α là góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \). Tìm cosα?

Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.

a) Chứng minh ΔABD = ΔEBD.

b) Chứng minh: DE = AD và DE vuông góc với BC.

c) Chứng minh: BD là đường trung trực của đoạn AE.

d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.

Một hình thoi có diện tích là 20cm², biết độ dài một đường chéo là 20 cm. Tính độ dài đường chéo còn lại.

Tìm phép dư trong phép chia đa thức f(x) = x²⁰²⁰ – 1 cho đa thức g(x) = x² + x + 1.

Tìm x biết: (x – 12) – 15 = 20 – (17 + x).

Tìm x biết: 720 : [41 – (2x – 5)] = 2³.5.

Cho tam giác ABC biết b = 7, c = 5, \(\)\[\cos \widehat A = \frac{3}{5}\]. Tính S, R, r.

Tìm nguyên hàm của hàm số \(\int {\frac{x}{{{{\sin }^2}x}}dx} \).

Cho tam giác ABC có AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính độ dài phân giác góc A?

Trong hệ trục tọa độ Oxy, cho đường thẳng d: y = 2x − 2 và điểm I(3; 2). Hãy tính khoảng cách:

a) Từ O đến d;

b) Từ I dến d.

90000m² =… hm².

Biểu đồ dưới đây nói về số học sinh tham gia tập bơi của khối lớp Bốn ở một trường tiểu học :

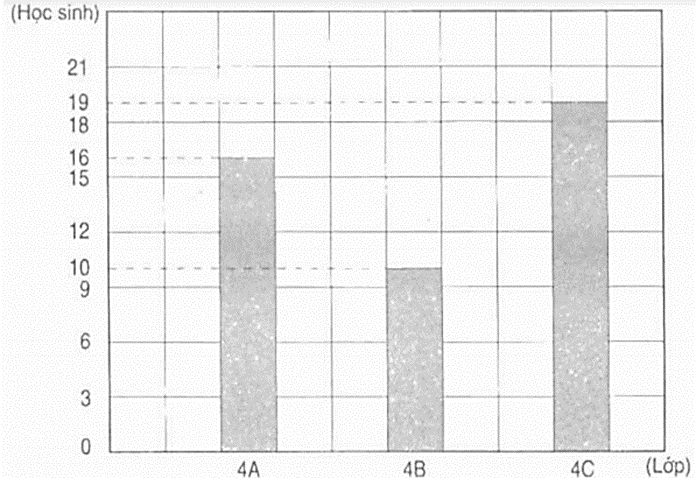
Dựa vào biểu đồ dưới đây hãy viết vào chỗ chấm :

a) Lớp 4A có ……… học sinh tập bơi

b) Lớp 4B có ……… học sinh tập bơi

c) Lớp ……… có nhiều học sinh tập bơi nhất

d) Số học sinh tập bơi của lớp 4B ít hơn lớp 4A là ………học sinh

e) Trung bình mỗi lớp có ……… học sinh tập bơi.

\[\frac{3}{5}\]ha = …m².

Phân tích các số sau ra thừa số nguyên tố và tìm xem mỗi số có bao nhiêu ước:

a) 320                   b) 625

c) 504                   d) 900          e) 3675.

Cho biết cosα = \(\frac{{ - 2}}{3}.\) Giá trị của P = \(\frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\) bằng bao nhiêu?

Hình ngũ giác là hình gì?

Cho đường tròn (O; R) đường kính AB, M là một điểm bất kì trên đường tròn (M khác A và B) tiếp tuyến cắt tại m cắt hai tiếp tuyến của A và B của đường tròn đã cho tại C và D. Chứng minh rằng: tứ giác AOMC và BOMD nội tiếp; \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).

Tìm x biết: –x – 14 + 32 = – 26.

Tìm x biết: 2x(3x + 5) – x(6x – 1) = 33.

Tất cả các giá trị của m để bất phương trình 2|x – m| + x² + 2 > 2mx thỏa mãn với mọi x là?

Cho tam giác ABC cân tại A có cạnh bên bằng 6 và \(\widehat {BAC} = 120^\circ \). Điểm M thuộc cạnh AB sao cho AM = \(\frac{1}{3}AB\) và N là trung điểm AC. Tính tích vô hướng \[\overrightarrow {BN} .\overrightarrow {CM} \].

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Cho tam giác ABC, lấy M,N,P sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NA} + 3\overrightarrow {NC} = \overrightarrow 0 ,\overrightarrow {PA} + \overrightarrow {PB} = \overrightarrow 0 \)

a) Tính \[\overrightarrow {PM} ,\overrightarrow {PN} \] theo \[\overrightarrow {AB} ,\overrightarrow {AC} \].

b) Chứng minh: M, N, P thẳng hàng.

Cho 4 điểm A, B, C, D bất kì.

a) Chứng minh: \[\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = \overrightarrow 0 \].

b) Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui".

Hình thang cân có độ dài hai cạnh đáy và chiều cao lần lượt là 40 m, 30 m và 25 m có diện tích là bao nhiêu?

Có bao nhiêu giá trị nguyên của m để phương trình \(\sqrt[3]{{m + 3\sqrt[3]{{m + 3\sin x}}}} = \sin x\) có nghiệm thực?

Một đoàn tàu dài 280m chạy qua một đường hầm dài 1200m trong 2 phút 30 giây với vận tốc đó tàu chạy quãng đường 159,84 km trong thời gian bao lâu?

Phân tích đa thức thành nhân tử: (3x + 2)(3x – 5)(x – 1)(9x + 10) + 24x².

Tìm GTLN của S = \(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)(a, b, c là 3 cạnh trong 1 tam giác và p là nửa chu vi).

Cho tam giác ABC vuông tại A (AB < AC) đường cao AH, gọi D là trung điểm của AC lấy E đối xứng H qua D .

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Qua A kẻ tia AI // HE cắt đường thẳng BC tại I. Chứng minh tứ giác AEHI là hình bình hành.

c) Trên tia đối của tia HA lấy K sao cho AH = HK. Chứng minh AK là tia phân giác của góc \(\widehat {IAC}\).

d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông , khi đó tứ giác AHCE là hình gì ?

Phép cộng, trừ 2 số cùng số mũ.

Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng tổng của chúng bằng 15 và tích của chúng bằng 105.

Tính chu vi và diện tích của mảnh đất hình chữ nhật biết chiều rộng của mảnh đất là 8,5m, chiều dài gấp đôi chiều rộng.

Mua ngẫu nhiên 1 tờ vé số có 6 chữ số. Tính xác suất trong các trường hợp sau:

a) Trúng giải tám (quay 1 lần, với 2 chữ số cuối cùng của tờ vé số khớp với 2 chữ số quay được.

b) Trúng giải khuyến khích cho các vé có 5 chữ số cuối cùng liên tiếp theo hàng thứ tự của giải đặc biệt.

Tìm x biết: (2x + 3)² – 4x(x + 4) = 25.

245 phút = …giờ… phút.

Bỏ ngoặc rồi tính 25 − ( − 17 ) + 24 – 12.

Tìm nghiệm nguyên của phương trình: 3x² – 2xy + y – 5x + 2 = 0.

435 phút = …giờ… phút.

Giải hệ phương trình: \(\left\{ \begin{array}{l}8\left( {{x^2} + {y^2}} \right) + 4xy + \frac{5}{{{{\left( {x + y} \right)}^2}}} = 13\\2y + \frac{1}{{x + y}} = 1\end{array} \right.\).

Phân tích đa thức thành nhân tử: 9x² – 36xy – 36y².

Biết rằng A : B = 8 : 3, A : C = 6 : 5 và A + B + C= 106. Tìm giá trị của B.

Biết rằng tổng của n số tự nhiên đầu tiên là 210, tìm giá trị của n.

Cho tam giác ABC có AB = 4, AC = 6 và \(\widehat {BAC} = 60^\circ \). Gọi M là trung điển của BC, điểm N thỏa mãn \(\overrightarrow {AN} = \frac{7}{{12}}\overrightarrow {AC} \). Chứng minh AM vuông góc BN.

Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.

a) Tứ giác AMBQ là hình gì?

b) Chứng minh rằng CH ⊥ AB.

c) Chứng minh tam giác PIQ cân.

Cho tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. Gọi M, N, P, Q lần lượt là trung điểm của OB, OC, AC, AB.

a) Chứng minh MNPQ là hình bình hành.

b) Xác định vị trí O để MNPQ là hình chữ nhật.

Cho tam giác ABC nhọn có trực tâm H. Chứng minh:

\(\tan A.\overrightarrow {HA} + \tan B.\overrightarrow {HB} + \tan C.\overrightarrow {HC} = \overrightarrow 0 \).

Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.

a) Chứng minh AH = DE.

b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.

c) Chứng minh O là trực tâm của tam giác ABQ.

d) Chứng minh S_ABC = 2S_DEQP.

Cho x > 0, tìm giá trị nhỏ nhất của M = \(4{x^2} - 3x + \frac{1}{{4x}} + 2021\).

Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có: MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Số 252 có bao nhiêu ước dương?

Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên.

Một hộp sữa hình trụ có bàn kính đáy bằng 6,5 cm. Biết diện tích vỏ hộp (kể cả nắp) là 292,5π cm². Tính thể tích của hộp sữa đó?

Một mảnh đất hình chữ nhật có chiều dài là 40m, chiều rộng bằng \(\frac{1}{2}\) chiều dài, trong đó diện tích đất làm nhà chiếm 30%. Tính:

a) Diện tích của mảnh đất đó.

b) Diện tích đất làm nhà là bao nhiêu mét vuông?

1 người gửi tiết kiệm 50000000 đồng với lãi suất là 0.6%/1 tháng . hỏi sau 1 tháng cả số tiền gửi và tiền lãi là bao nhiêu là bao nhiêu?

Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là \(\frac{{n\left( {n - 3} \right)}}{2}\).

Theo biểu giá bán lẻ xăng dầu một lít xăng RON 95 – IV có giá 18000 đồng. Do ảnh hưởng dịch Covid – 19 , giá xăng giảm 20 %. Sau đó lại điều chỉnh giảm giá tiếp 10% . Hỏi sau 2 lần điều chỉnh giá xăng là bao nhiêu?

Tìm x biết:

a) 2075 : 5 = x . 75 : 5 + 40.

b) x + x : 5 . 7,5 + x : 2 . 9 = 315.

Tính bằng cách thuận tiện nhất 46 : 24 + 8 : 24.

Tìm nghiệm nguyên của phương trình: x² + x + 2009 = y².

Tìm giá trị nhỏ nhất của A = x⁴ – 3x³ + 4x² – 3x + 10.

Xếp ngẫu nhiên ba bạn nam và ba bạn nữ ngồi thành sáu ghế kê theo hàng ngang. Tìm xác suất cho:

a) Nam, nữ ngồi xen kẽ nhau.

b) Ba bạn nam ngồi bên cạnh nhau.

Tìm cặp số tự nhiên x,y biết: 6xy – 9x – 4y + 5 = 0.

Một tấm vải dài 105 m . Nếu cắt đi \(\frac{1}{9}\) tấm vải thứ nhất ,\(\frac{3}{7}\) tấm vải thứ hai và \(\frac{1}{3}\) tấm vải thứ ba thì phần còn lại của ba tấm vải bằng nhau. Hỏi mỗi tấm vải dài bao nhiêu mét?

Cho α là góc tù và sinα – cosα = \(\frac{4}{5}\). Giá trị của M = sinα – 2cosα là ?

Cho các số 13,1; 13,01; 1,30.10³; 1.3.10^–3. Có mấy số có ba chữ số có nghĩa?

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy, SA hợp với (SBC) một góc 45°. Tính thể tích hình chóp S.ABC.

Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:
a) Tứ giác ABHM nội tiếp.
b) OA.OB = OH.OM = R².
c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.

Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.

a) Chứng minh: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \).

b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\overrightarrow {C'A'} \).

Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.

a) Chứng minh: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \).

b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\overrightarrow {C'A'} \).