7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 59)

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, \(\widehat {BAD} = 60^\circ ,\) \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}.\) Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đấy đúng?

Một chi đoàn có 16 đoàn viên. Cần bầu chọn một Ban chấp hành ba người gồm Bí thư, Phó Bí thư và Ủy viên. Số cách chọn ra Ban chấp hành nói trên là:

Cho hàm số \(y = {x^3} - 3mx + 1.\) Tìm m để đồ thị hàm số có hai điểm cực trị B và C sao cho tam giác ABC cân tại A, với A(2, 3).

Giá trị nhỏ nhất của f(x) = x³ – 3x trên đoạn [-3; 3] bằng

Tìm x, biết: \(3\sqrt {x - 2} - \sqrt {{x^2} - 4} = 0.\)

Có 5 cái bánh, chia đều cho 8 em. Hỏi mỗi em được bao nhiêu phần cái bánh?

Tìm tất cả các số a trong khai triển của (1 + ax)(1 + x)⁴ có chứa số hạng 22x³.

Trong khai triển (1 – 3x)ⁿ = a₀ + a₁x + a₂x² + ... + a_nxⁿ. Tìm a₂ biết a₀ – a₁ + a₂ – a₃ + ... + (-1)ⁿa_n = 2²⁰¹⁸.

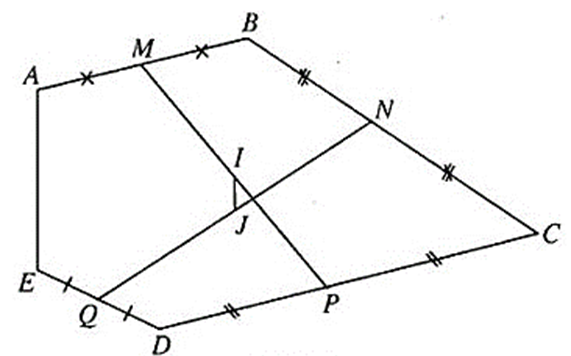
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm MP, NQ. Chứng minh IJ // AE và AE = 4IJ.

Tìm hệ số của x⁴ trong khai triển của biểu thức (x + 3)⁶.

Tìm số hạng đứng giữa trong khai triển (x³ + xy)²¹.

Tìm tất cả các giá trị của tham số m để phương trình \[{4^{x\, + \,1}} - {2^{x\, + \,2}} + m = 0\] có nghiệm.

Cho (O, R), lấy điểm A cách O một khoảng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.

a) Chứng minh tam giác OBA vuông tại B và tam giác OAK cân tại K.

b) Đường thẳng KI cắt AB tại M. Chứng minh KM là tiếp tuyến của đường tròn (O).

Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm \(f'\left( x \right)\) thỏa mãn \(f'\left( x \right) = \left( {1 - x} \right)\left( {x + 2} \right)g\left( x \right) + 2018\) trong đó g(x) < 0, ∀x ∈ ℝ. Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?

Cho hàm số \(y = \sqrt {\left( {2m - 1} \right)\sin x - \left( {m + 2} \right)\cos x + 4m - 3} \) (1). Có tất cả bao nhiêu giá trị nguyên dương nhỏ hơn 2019 của tham số m để hàm số (1) xác định với mọi x ∈ ℝ?

Cho hình chóp S.ABC có SA = SB = SC = \(a\sqrt 3 ,\) AB = AC = 2a, BC = 3a. Thể tích của khối chóp S.ABC bằng

Cho hình chóp tam giác S.ABC, gọi M, N lần lượt là trung điểm của SB và SC. Tính tỉ số thể tích của khối chóp S.AMN và S.ABC.

Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm nằm trên cạnh AB sao cho \(AP = \frac{1}{3}AB.\) Gọi Q là giao điểm của SC và (MNP). Tính tỉ số \(\frac{{SQ}}{{SC}}.\)

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng (α) đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số \(\frac{{SN}}{{SD}}\) để (α) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

Cho hình trụ có hai đáy là hai hình tròn (O; R) và (O′; R). AB là một dây cung của đường tròn (O; R) sao cho tam giác O′AB là tam giác đều và mặt phẳng (O′AB) tạo với mặt phẳng chứa đường tròn (O; R) một góc \(60^\circ .\) Tính theo R thể tích V của khối trụ đã cho.

Cho hình vuông ABCD cạnh a. Tính \(\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right).\)

Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng \(\overrightarrow {AC} \,.\,\overrightarrow {BD} .\)

Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AD. Gọi G là trọng tâm tam giác SCD. Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (ABG) là:

Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm của các cạnh AC, BC. Trong tam giác BCD lấy điểm M sao cho hai đường thẳng KM và CD cắt nhau tại I. Tìm thiết diện của tứ diện với (HKM) trong hai trường hợp:

a) I nằm ngoài đoạn CD.

b) I nằm trong đoạn CD.

Cho tam giác ABC có \(\widehat A = 120^\circ ,\) AB = AC = a. Quay tam giác ABC (bao gồm điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:

Tính tổng \(S = C_n^0 + C_n^1 + ... + C_n^n.\)

Tìm tất cả các giá trị của tham số m để phương trình x⁴ – 10x² + m = 0 có 4 nghiệm phân biệt lập thành một cấp số cộng.

Gieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 7.

b) Các mặt xuất hiện có số chấm bằng nhau.

Người ta dùng 100m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.

Cho hàm số \(y = x\sqrt {4 - {x^2}} .\) Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m.

Hỏi có bao nhiêu giá trị m nguyên trong [-2017; 2017] để phương trình log(mx) = 2.log(x + 1) có nghiệm duy nhất?

Biết phương trình \(\log _2^2x - 2{\log _2}\left( {2x} \right) - 1 = 0\) có hai nghiệm x₁, x₂. Tính x₁x₂.

Một tam giác ABC có số đo góc đỉnh A là \(60^\circ .\) Biết số đo góc B là một nghiệm của phương trình \({\sin ^2}4x + 2\sin 4x.\cos 4x - {\cos ^2}4x = 0.\) Tìm số tam giác thỏa mãn yêu cầu bài toán.

Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng cả ba viên vòng 10 là 0,0008; xác suất đề một viên trúng vòng 8 là 0,15; xác suất để một viên trúng vòng dưới 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Xác suất để vận động viên đó đạt ít nhất 28 điểm có giá trị gần bằng nhất với số nào sau đây?

Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số là

Phương trình \(\left( {{2^x} - 5} \right)\left( {{{\log }_2}x - 3} \right) = 0\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right).\) Tính giá trị của biểu thức \(K = {x_1} + 3{x_2}.\)

Tìm số tiệm cận của đồ thị hàm số \(y = \frac{{{x^2} - 6x + 3}}{{{x^2} - 3x + 2}}.\)

Tìm giá trị thực của tham số m để hàm số \(y = - {x^3} - 3{x^2} + m\) có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.

Tìm tất cả các giá trị của tham số m để phương trình \(4{\left( {{{\log }_2}\sqrt x } \right)^2} - {\log _{\frac{1}{2}}}x\) + m = 0 có nghiệm thuộc khoảng (0; 1).

Tìm tập nghiệm của phương trình \({9^x} - {4.3^x} + 3 = 0.\)

Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số có 5 chữ số khác nhau mà số đó nhất thiết có mặt các chữ số 1, 2, 5?