7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 54)
48 câu hỏi
Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?
15
14
13
12.
Tìm m để \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có cực trị và khoảng cách giữa 2 điểm cực trị bằng 10.
Phân tích đa thức thành nhân tử (x + y)3 – ( x – y)3.
Phân tích đa thức sau thành nhân tử: x2 + 6x + 9.
Cho \(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)
a) Tìm điều kiện xác định rồi rút gọn A
b) Tìm a để \[{\rm{A}} < \frac{1}{3}\].
Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x2 + y2 – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:
\({\left( {x + 2} \right)^2} + {y^2} = \sqrt 6 \)
\({\left( {x - 2} \right)^2} + {y^2} = 6\)
x2 + y2 – 2x – 5 = 0
2x2 + 2y2 – 8x + 4 = 0.
Tìm giá trị nhỏ nhất của hàm số \(y = 3{\rm{x}} + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
Cho hàm số \((C):y = \frac{{x + 2}}{{x - 1}}\)
Cho điểm M(0; m). Xác định m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho 2 tiếp tuyến tương ứng nằm về hai phía đối với trục Ox.
Tìm các số nguyên x, y thỏa mãn x3 + 2x2 + 3x + 2 = y3.
Tập xác định của hàm số y = logx là:
[0; +∞)
(0; +∞)
(–∞; +∞)
[10; +∞).
Cho các số dương x, y, z thỏa mãn điều kiện xy + yz + zx = xyz. Chứng minh rằng:
\(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \).
Giải hệ phương trình \(\left\{ \begin{array}{l}y + x{y^2} = 6{{\rm{x}}^2}\\1 + {x^2}{y^2} = 5{{\rm{x}}^2}\end{array} \right.\).
Đạo hàm của hàm số y = log(1 – x) bằng:
\(\frac{1}{{\left( {x - 1} \right)\ln 10}}\)
\(\frac{1}{{x - 1}}\)
\(\frac{1}{{1 - x}}\)
\(\frac{1}{{\left( {1 - x} \right)\ln 10}}\).
Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
xm . yn = (xy)m+n
(xy)n = xn . yn
xm . xn = xm+n
(xm)n = xmn.
Hình bình hành ABCD có AC ⊥ AD và AD = 3,5; \(\widehat D = 50^\circ \). Tính diện tích ABCD.
Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)
\(m \ge \frac{4}{3}\)
\(m \le \frac{4}{3}\)
\(m \ge \frac{1}{3}\)
\(m \le \frac{1}{3}\).
Chứng minh bất đẳng thức sinx < x với mọi x > 0 và sinx > x với mọi x < 0.
Cho hàm số y = – x3 + 3x2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
m < 1
m ≥ 1
m ≤ –1
m ≥ –1.
Tính tổng: S = 12 + 22 + 32 + ... + n2.
Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a2. Chứng minh rằng sinB.sinC = sin2A và hb . hc = ha2.
Cho 4 chữ số 1, 5, 8, 9 có thể viết được mấy số có 4 chữ số khác nhau từ các chữ số trên.
Tìm x biết x² – 9 + 5(x – 3) = 0.
Thực hiện phép tính: (102 + 112 + 122) : (132 + 142).
Tìm x biết (8x – 7)(8x – 5)(2x – 1)(4x – 1) = 9.
Trong các mệnh đề sau, mệnh đề nào đúng?
∀ n ∈ ℕ, n2 + 1 không chia hết cho 3
∀ n ∈ ℝ, |x| < 3 ⇔ x < 3
∀ n ∈ ℝ, (x – 1)2 ≠ x – 1
∃ n ∈ ℕ, n2 + 1 chia hết cho 4.
Tính \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\).
Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?
P = 3
P = 1
P = 9
\(P = \frac{1}{3}\).
Cho Ax, By là các tiếp tuyến của \(\left( {O;\frac{{AB}}{2}} \right)\). Tiếp tuyến tại M của (O) cắt Ax, By, AB lần lượt tại C, D, E. AD và BC cắt nhau tại N
a) Tính AC. BD theo AB
b) Chứng minh MN vuông góc AB
c) So sánh 2 tỉ số \(\frac{{CM}}{{CE}};\frac{{DM}}{{DE}}\).
d) Chứng minh rằng đường thẳng EN đi qua trung điểm của các đoạn thẳng AC, BD.
Phân tích đa thức thành nhân tử: (x – 1)(x – 2)(x + 7)(x + 8) + 8.
Khai triển (x – 2)2.
Chứng minh với ab ≥ 1 thì \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\).
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng:
\(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. Gọi I và J lần lượt là trung điểm của MP và NQ. Chứng minh IJ song song với AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
a) AB2 = BH . BC
b) AC2 = CH . BC
c) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).
Chứng minh với x, y, z dương ta có \(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} \ge x + y + z\).
Với a, b, c là các số dương, chứng minh rằng
\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).
Tìm giá trị nhỏ nhất của x2 + 3x + 4.
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
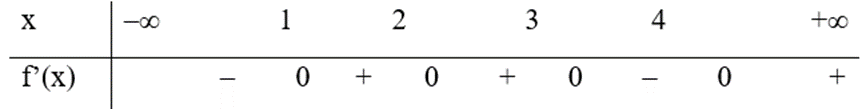
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
(1; +∞)
(–∞; –1)
(–1; 0)
(0; 2).
Tổng các nghiệm của phương trình 3x+1 + 31-x = 10.
1
3
–1
0.
Rút gọn các phân thức sau:
a) \(\frac{{{y^3} - {x^3}}}{{{x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}}}\)
b) \(\frac{{{x^5} + x + 1}}{{{x^3} + {x^2} + x}}\)
c) \(\frac{{2{{\rm{x}}^2} - x - 3}}{{{x^2} - 4x - 5}}\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao tuyến của (SAC) và (SBD)
b) Tìm giao điểm DN với (SAC)
c) Chứng minh MN // (SCD).
Mệnh đề nào sau đây đúng ?
Có duy nhất một vectơ cùng phương với mọi vectơ.
Có ít nhất hai vectơ cùng phương với mọi vectơ.
Có vô số vectơ cùng phương với mọi vectơ.
Không có vectơ nào cùng phương với mọi vectơ.
Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử:
x2 – 2x – 4y2 – 4y.
Phân tích đa thức thành nhân tử: x3 – 7x – 6.
Chứng minh \(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\) với a, b, c ≥ 1.
Cho A = 5n+2 + 26 . 5n + 82n + 1. Chứng minh A ⋮ 59.
Cho x > 0, y > 0 và x + y = 1. Chứng minh: \(8\left( {{x^4} + {y^4}} \right) + \frac{1}{{xy}} \ge 5\).
Chứng minh rằng a4 + b4 + c4 ≥ abc(a + b + c).








