7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 51)

Tính bằng cách thuận tiện: \(\frac{1}{4}:0,25 - \frac{1}{8}:0,125 + \frac{1}{2}:0,5 - \frac{1}{{10}}\).

Xe thứ nhất chở được 25 tấn hàng, xe thứ hai chở 35 tấn hàng, xe thứ ba chở bằng trung bình cộng 3 xe. Hỏi xe thứ 3 chở bao nhiêu tấn hàng?

A = {1; 2; 3; …; 16}. Bốc ngẫu nhiên 3 phần tử trong A. Tính xác suất để để tổng 3 số bốc ra chia hết cho 3.

Cho tứ diện ABCD có AB = AC = BC = 2; AD = 4; \(\widehat {BAD} = \widehat {CAD} = 60^\circ \). Tính thể tích khối tứ diện ABCD?

Chứng minh rằng không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \sin x\).

Một hình vuông A có diện tích bằng \(\frac{1}{9}\) diện tích của hình vuông B cạnh \(\frac{3}{5}dm\). Tính cạnh hình vuông A.

Một cửa hàng có 3,125 tấn gạo. Ngày thứ nhất bán được 24%số gạo. Ngày thứ hai bán được 32% số gạo còn lại. Hỏi ngày thứ hai cửa hàng bán được bao nhiêu ki lô gam gạo?

Trong mặt phẳng Oxy cho hai điểm A(0; 2) và B(4; 1). Điểm N(2; –3) là ảnh của M qua phép tịnh tiến theo vectơ \(\overrightarrow {AB} \). Tìm tọa độ điểm M?

Cho phương trình: x² – 5x + m – 1 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm phân biệt x₁; x₂ sao cho: \(2{x_2} = \sqrt {{x_1}} \).

Trung bình cộng số ngô ở hai thùng là 225 kg .Thùng B nhiều hơn thùng A là 120 kg. Tìm tỉ số phần trăm số ngô giữa thùng A và thùng B.

Cho hình vẽ, có \(\widehat {BAC}\) = 50°, \(\widehat {ABC}\) = 65°, Ax // BC.

a) Tính số đo \(\widehat {ACB}\).

b) Tính số đo \(\widehat {yAx}\) rồi chứng minh Ax là tia phân giác của \(\widehat {yAC}\).

c) Vẽ tia Az là tia đối của tia Ax, tia Am là tia phân giác của zAB, tia Bn là tia phân giác của \(\widehat {ABC}\). Chứng minh Am // Bn.

Cho a thỏa mãn a² – 5a + 2 = 0. Tìm giá trị biểu thức: P = a⁵ – a⁴ – 18a³ + 9a² – 5a + 2017 + (a⁴ – 40a² + 4) : a².

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD =MB.

1) Chứng minh AD = BC.

2) Chứng minh CD vuông góc với AC.

3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh tam giác ABM = tam giác CNM.

Cho tam giác ABC nhọn có BC = 3a và bán kính đường tròn ngoại tiếp tam giác ABC là R = \(a\sqrt 3 \). Tính số đo góc \(\widehat A\).

Cho đường tròn tâm (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Tìm x, y, z biết 2x = 3y; 4y = 3z và x – y + 2z = 57.

Trong khai triển (a+b)ⁿ, xác định số hạng tổng quát của khai triển.

Một mảnh đất hình chữ nhật có chiều dài 36m, chiều rộng bằng \(\frac{3}{4}\) chiều dài. Người ta dành 25% diện tích để trồng rau. Hỏi diện tích phần đất còn lại là bao nhiêu?

Tìm x biết: \(\frac{3}{7} - \frac{4}{7}:\left( {x - 1} \right) = \frac{5}{7}\).

Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn hệ thức \(\left| {4\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {2\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} } \right|\).

Hai tập hợp A = (–3; 5], B = [3a – 5; + ∞). Tìm a để A giao B có 1 phần tử?

Tìm GTNN của \(B = - 13 + \left| {2,34 - 3x} \right|\).

Cho hình chữ nhật ABCD có AB = 3cm; BC = 5cm. Tính độ dài véctơ \(\overrightarrow {AC} \)?

Cho hệ phương trình: \(\left\{ \begin{array}{l}mx + y = 2m\\x + my = m + 1\end{array} \right.\).

 Tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất (x; y) là các số nguyên.

Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N là điểm chính giữa cung AB, cung BC; AN cắt CM tại I. Chứng minh:

a) Tam giác BNI cân.

b) Gọi NM cắt AB tại K. Chứng minh IK // BC.

Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ \(\overrightarrow {AG} \).

Cho điểm A nằm ngoài đường tròn (O; R). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).

a) Chứng minh rằng: OA vuông góc BC và OA // BD.

b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE. AD = AH. AO.

Cho đường tròn (O), đường kính AB, điểm M nằm trên (O). Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.

a) Chứng minh rằng NE ⊥ AB.

b) Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O).

c) Chứng minh rằng FN là tiếp tuyến của đường tròn (B; BA).

Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn với (E; F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của (O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chọn câu đúng:

Cài đặt hiển thị FIX trên máy tính casio fx–580VNX.

Cho (O) và điểm A nằm ngoài đường tròn. Vẽ cách tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm DE.

a) Chứng minh: A,B,H,O,C cùng nằm trên một đường tròn.

b) Chứng minh: HA là phân giác của BHC.

c) Gọi I là giao điểm của BC và DE. Chứng minh: AB² = AI . AH.

d) BH cắt (O) ở K. Chứng minh: AE // CK.

Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?

Số các giá trị nguyên âm của tham số m để tập xác định của hàm số \(y = \frac{2}{{x - 2m}} + \sqrt {7m + 1 - 2x} \) chứa đoạn [–1; 1]?

Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = sin 3x + cos 3x.

Hai chiếc thuyền khởi hành tại cùng một vị trí A đi thẳng theo hai hướng tạo với nhau 1 góc 30° hỏi sau 2 giờ hai thuyền cách nhau bao xa, biết thuyền B chay với vận tốc 50 km/h, thuyền C chạy với vận tốc 60 km/h.(kết quả làm tròn đến 1 số thập phân)

Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.

a) Chứng minh OM // (SCD).

b) Xác định giao điểm N của MD và mặt phẳng (SBC).

Một căn phòng hình chữ nhật có chiều rộng 6m, chiều dài gấp rưỡi chiều rộng. Người ta lát nền căn phòng đó bằng loại gạch vuông cạnh 3dm . Hỏi căn phòng đó lát nền hết bao nhiêu viên gạch ?

Một lớp có 25% học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Tính số học sinh của lớp đó biết số học sinh trung bình là 5 em?

Năm ngoái, mẹ đi chợ mua 5 gói bánh quy hết 100000 đồng. Năm nay vẫn số tiền đó mẹ mua được 4 gói bánh quy. Hỏi năm nay giá một gói bánh quy tăng hay giảm bao nhiêu phần trăm?

Một cửa hàng bán một chiếc xe đạp với giá 1495000 đồng thì được lãi 15% so với tiền vốn mua xe đạp đó.hỏi tiền vốn mua chiếc xe của cửa hàng đó là bao nhiêu?

Phép chiếu xuyên tâm có đặc điểm gì?

Cho mặt cầu S(O; R) và một điểm A, biết OA = 2R. Qua A kẻ cát tuyến cắt (S) tại B và C sao cho BC = \(R\sqrt 3 \). Tính khoảng cách từ O đến BC.

Cho tam giác ABC, trực tâm H, M là trung điểm BC. Chứng minh \(\overrightarrow {MH} .\overrightarrow {MA} = \frac{1}{4}B{C^2}\).

Cho tam giác vuông có độ dài cạnh huyền là 15 cm độ dài cạnh góc vuông là 9 cm. Tính chu vi và diện tích tam giác đó.

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A kẻ tiếp tuyến AM, AN tới đường tròn (O) (M, N là các tiếp điểm).

a) Chứng minh rằng tứ giác AMON nội tiếp.

b) Vẽ cát tuyến ABC tới đường tròn (O) (Tia AO nằm giữa AM và tia AC).

Chứng minh rằng AM² = AB.AC.

c) Gọi H là giao điểm AO và MN. Chứng minh rằng tứ giác BHOC nội tiếp.

Để đo chiều cao h của cổng parabol của trường ĐHBK Hà Nội, người ta đo khoảng cách giữa 2 chân cổng được L = 9 m, người ta thấy nếu đứng cách chân cổng 0,5 m thì đầu chạm cổng, biết người này cao 1,6 m. Tính chiều cao của cổng.

Tìm nghiệm dương nhỏ nhất của phương trình sin2x – 2(sinx – cosx) – 2 = 0.

Tìm số tự nhiên x biết 3(x + 1) + 25 chia hết cho 5 và 8 < x < 16.

Phân tích đa thức thành nhân tử: 5xy⁴ + 15x⁴y + 15x²y³ + 5x³y².

Nêu chiều của đường tròn lượng giác.

Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Hãy so sánh các cung nhỏ AB, AC và BC biết \(\widehat A = 50^\circ \).

Cho đường tròn (O; R), đường kính AB. Lấy điểm C tùy ý trên cung AB sao cho AB < AC.

a) Chứng minh tam giác ABC vuông.

b) Qua A vẽ tiếp tuyến (d) với đường tròn (O), BC cắt (d) tại F. Qua C vẽ tiếp tuyến (d’) với đường tròn (O), (d’) cắt (d) tại D. Chứng minh : DA = DF.

c) Hạ CH vuông góc AB (H thuộc AB), BD cắt CH tại K. Chứng minh K là trung điểm CH.

d) Tia AK cắt DC tại E. Chứng minh EB là tiếp tuyến của (O)

Có bao nhiêu cách sắp xếp 5 bạn nam và 2 bạn nữ thành 1 hàng dọc theo thứ tự bất kì?

Rút gọn: \(\sqrt {7 + 4\sqrt 3 } + \sqrt {7 - 4\sqrt 3 } \).

Cửa hàng lấy 1 thùng nước ngọt (24 lon)của đại lý phân phối với giá 192.000 đồng và bán lẻ với giá 10.000 đồng/ lon.

a) Hỏi khi bán hết 1 barrel nước ngọt thì cửa hàng thu được lãi bao nhiêu % so với giá gốc?
b) Trong đợt khuyến mãi, do đại lý phân phối giảm giá nên cửa hàng cũng giảm còn 9.500 đồng/ lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua 1 barrel nước ngọt với giá bao nhiêu?

Mỗi tháng mẹ bạn Hà được nhận 7 000 000 đồng tiền lương, mẹ đã mua có thực phẩm cho gia đình hết 5 600 000 đồng. Hỏi mẹ là mua thực phẩm hết bao nhiêu phần trăm số tiền lương?

Giải phương trình: sin5x + 2cos²x = 1.

Một cửa hàng thời trang nhập 100 cái áo với giá vốn mỗi chiếc 200000 đồng. Chi phí vận chuyển là 1000000 đồng. Hỏi cửa hàng bỏ ra bao nhiêu tiền vốn để nhập 100 cái áo?

Tìm số tự nhiên n để 3n + 16 chia hết cho n + 4.

Tìm tất cả các giá trị của tham số thực m để hàm số y = mx³ − 2mx² + (m − 2)x + 1 không có cực trị.

Từ điểm M ở ngoài đường tròn (O) vẽ 2 tiếp tuyến MA, MB đến (O), cát tuyến MCD với (O) (AB là các tiếp điểm và O nằm trong góc BMD.

a) Chứng minh: tứ giác AOBM nội tiếp và xác định tâm G của đường tròn ngoại tiếp.

b) Chứng minh: MA² = MC.MD.

c) Gọi I là trung điểm của CD. Chứng minh: 5 điểm M,A,O,I,B cùng nằm trên 1 đường tròn.

d) Gọi H là giao điểm của AB và MO. Chứng minh: Tứ giác CHOD nội tiếp.

e) Vẽ dây BE của (O) song song với CD. Chứng minh: 3 điểm E, I, A thẳng hàng.

Người ta lấy ra 15kg gạo trong một bao gạo là 75% lượng gạo trong bao đó. Lúc đầu bao đó có bao nhiêu kilôgam gạo?

Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:

a, Tam giác BDI là tam giác cân.

b, DE là đường trung trực của IC.

c, IF và BC song song, trong đó F là giao điểm của DE và AC.

Tính bán kính đường tròn ngoại tiếp tam giác đều cạnh a.

Hình thang có đáy lớn hơn đáy bé 20,4 dm và bằng \(\frac{5}{3}\) đáy bé, chiều cao hơn đáy bé 2,1 dm. Tính diện tích hình thang.

Tìm nghiệm nguyên dương của phương trình x + y + z = 2xyz.

Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC có A(–1;1), B(1;3) và trọng tân là G\(\left( { - 2;\frac{2}{3}} \right)\). Tìm tọa độ điểm M trên tia Oy sao cho tam giác MBC vuông tại M.

Thực hiện phép tính: \(A = \frac{{{2^{12}}{{.3}^5} - {4^6}{{.9}^2}}}{{{{\left( {{2^2}.3} \right)}^6} + {8^4}{{.3}^5}}} + \frac{{{5^{10}}{{.7}^3} + {{25}^5}{{.49}^2}}}{{{{\left( {125.7} \right)}^3} + {5^9}{{.14}^3}}}\).

Tính diện tích hình thang có đáy lớn 54m, đáy bé bằng \(\frac{2}{3}\) đáy lớn và bằng \(\frac{3}{2}\) chiều cao.

Hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.

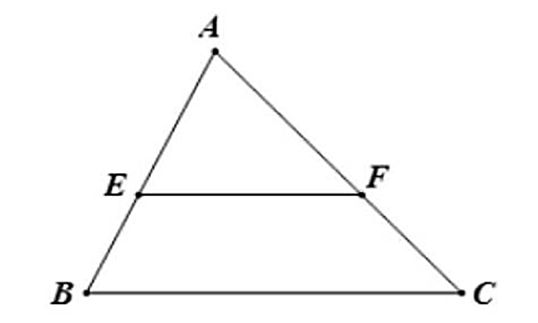
Cho ∆AEF ∽ ∆ABC (hình vẽ) nếu AE = 3cm; EB = 2cm; AF = 4cm, thì FC bằng bao nhiêu?

Xếp ngẫu nhiên 4 quyển sách Toán khác nhau và 4 quyển sách Hóa giống nhau vào một giá sách nằm ngang có 10 ô trống, mỗi quyển sách được xếp vào một ô. Xác suất để 4 quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau bằng?

Lãi suất tiết kiệm là 0,58% một tháng. Một người gửi tiết kiệm 6000000 đồng. Hỏi sau 1 tháng cả số tiền gửi và tiền lãi là bao nhiêu?

Một đám đất hình chữ nhật có chiều dài 17,5m chiều rộng bằng \(\frac{3}{5}\)chiều dài                                    

a)Tính diện tích đám đất.               

b)Người khác đã dành 40% diện tích đám đất đó để trồng hoa. Hỏi diện tích trồng hoa là bao nhiêu mét vuông?    

Tính diện tích hình thang có đáy bé bằng 40cm, chiều cao bằng 30% đáy bé và và bằng 20% đáy lớn.

Tính diện tích hình thang có đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy bé kém đáy lớn 12 dm.

Tính diện tích hình thang có đáy lớn bằng 25 m, chiều cao bằng 80% đáy lớn, đáy bé bằng 90% chiều cao.

Từ 10 điểm phân biệt trên 1 đường tròn. Có bao nhiêu véctơ có gốc và ngọn trùng với 2 trong số 10 điểm đã cho

Tìm cấp số nhân biết: \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 14\\{u_1}{u_2}{u_3} = 64\end{array} \right.\).

Chứng minh (x + y)² ≥ 4xy với x, y > 0.

Xác định hệ số a và b để 2x² + ax + 5 chia hết cho x + 3 dư 41.

Cho a, b, c khác nhau đôi một, chứng minh rằng:

\(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\).

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a. Mặt phẳng (SBC) vuông góc với (ABC). Biết SB = \(2a\sqrt 3 \) và \(\widehat {SBC} = 30^\circ \). Tính khoảng cách từ B đến (SAC) theo a.

Cho hình vuông ABCD cạnh a. Gọi M, N lần lượt thuộc đoạn BC, AC sao cho: \(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {MC} ;\overrightarrow {CN} = k\overrightarrow {AN} \). Tìm k sao cho AM vuông góc với DN.

Có bao nhiêu cách xếp 3 bạn nam và 7 bạn nữ thành một hàng dọc sao cho các bạn nam không đứng cạnh nhau?

Hình thang có diện tích 540 cm², chiều cao 24 cm. Tính độ dài mỗi đáy của hình thang đó, biết đáy bé bằng \(\frac{4}{5}\) đáy lớn.

Tính \[\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x - 1} - \sqrt x } \right)\].

Tính bằng cách thuận tiện nhất: 57 . 0,1 . 100 . (2,5 . 4 – 10).

Tìm số hạng chứa x⁶ trong khai triển (2x – 1)⁶ (x² – x + \(\frac{1}{4}\)).

Tính giá trị biểu thức: 140 : 2,8 – 2,3.

Tìm các số x , y , z biết \(\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z - 3}}{4}\) và 2x + 3y – z = 45.

Cho tam giác ABC có AB – 4, AC = 5 và góc \(\widehat A = 60^\circ \). Phép đồng dạng tỉ số k = 2 biến A thành A', B thành B', C thành C'. Khi đó diện tích tam giác A'B'C' là?

Cho \(D = \frac{5}{{6.37}} + \frac{1}{{6.43}} + \frac{6}{{7.43}} + \frac{{10}}{{7.59}}\) và \(E = \frac{8}{{9.37}} + \frac{2}{{9.47}} + \frac{3}{{10.47}} + \frac{9}{{10.59}}\). Tính \(\frac{D}{E}\)?

Tính \(E = \frac{1}{{10}} + \frac{1}{{100}} + \frac{1}{{1000}} + \frac{1}{{10000}} + \frac{1}{{100000}} + \frac{1}{{1000000}}\).

Giải phương trình: 4x⁴ + 12x³ + 5x² – 6x – 15 = 0.

Ba tổ sản xuất cùng làm một số sản phẩm như nhau. Tổ 1 làm trong 2 giờ, tổ 2 làm trong 3 giờ, tổ 3 làm trong 5 giờ thì hoàn thanh xong công việc. Hỏi mỗi tổ có bao nhiêu người, biết tổ 3 làm ít hơn tổ 2 là 8 người và năng suất lao động của mỗi người là như nhau?

Cho hình chữ nhật ABCD với AD < AB. Gọi E là điểm nằm trên đường chéo BD (0 < BE < ED). Vẽ điểm F đối xứng với điểm C qua điểm E. Gọi H và K theo thứ tự là hình chiếu của F trên các đường thẳng AD, AB. Gọi O là giao điểm của BD, AC. Chứng minh rằng:

1) Tứ giác FHAK là hình chữ nhật.

2) FA // BD.

3) Ba điểm E, H, K thẳng hàng.

Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND. Tính \(\widehat {BMN}\).

Cho tam giác ABC, M và N là hai điểm thỏa mãn \(\overrightarrow {BM} = \overrightarrow {BC} - 2\overrightarrow {AB} ,\overrightarrow {CN} = x\overrightarrow {AC} - \overrightarrow {BC} \). Xác định x để A, M, N thẳng hàng.

Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB. Vẽ MF vuông góc BC tại F, ME vuông góc AC tại E. Gọi D là trung điểm AB. Chứng minh rằng tam giác DEF vuông cân. 

Cho tam giác ABC vuông tại A; AB = 6; AC = 8. Phép vị tự tâm A tỷ số \(\frac{3}{2}\) đến B thành B'; biến C thành C' tính bán kính R của đường tròn ngoại tiếp tam giác AB'C'.

Cho tam giác ABC vuông ở A(AB<AC ) đường cao AH . Gọi D là điểm đối xứng của A qua H . Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt là ở M và N . Chứng minh:

a, Tứ giác ABDM là hình thoi

b, AM vuông góc với CD .

Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng 1\(\frac{1}{2}\) số đo của cung lớn AB. Tính diện tích của tam giác AOB.

Chọn ngẫu nhiên 2 số khác nhau từ 30 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng?

Có bao nhiêu giá trị nguyên của tham số (m ) thuộc đoạn [– 2018; 2018] để phương trình (m + 1)(sin²x – sin 2x + cos 2x) = 0 có nghiệm.

Có bao nhiêu số tự nhiên có 3 chữ số khác nhau nhỏ hơn 345?

Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I. Gọi giao điểm BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.

Cho ΔMNP có I là trung điểm cạnh NP. Trên tia đối của IM lấy D sao cho IM = ID.

a) Chứng minh ΔMIN = ΔDIP.

b) Chứng minh MN // DP.

c) Gọi H là trung điểm MN, vẽ E sao cho H là trung điểm của PE. Chứng minh N là trung điểm của ED.

Một vườn cây có 840 cây, trong đó có 672 cây lấy gỗ và còn lại là cây ăn quả.

a) Số cây lấy gỗ chiếm bao nhiêu phần trăm số cây trong vườn?

b) Tìm tỉ số phần trăm giữa số cây ăn quả và số cây lấy gỗ?

Quy đồng mẫu số 3 phân số \(\frac{7}{9};\frac{8}{{15}};\frac{2}{{45}}\) với mẫu số chung nhỏ nhất?

Có bao nhiêu số tự nhiên gồm 5 chữ số chia hết cho 10?

Cho ngũ giác đều ABCDE và một điểm S không nằm trên mặt phẳng chứa ABCDE. Từ 6 điểm trên xác định bao nhiêu mặt phẳng?

Số nghiệm của phương trình \(\frac{{\sin 3x}}{{\cos x + 1}} = 0\) thuộc đoạn [2π,4π] là bao nhiêu?

Hình chữ nhật , hình bình hành, hình thang cân , hình vuông , hình thoi . Mỗi hình có bao nhiêu tâm đối xứng , trục đối xứng.

Tính bằng cách thuận tiện: 0,2468 + 0,08 . 0,4 . 12,5 . 2,5 + 0,7532.

Cho \(\frac{x}{5} = \frac{y}{7}\) và x – y = – 22. Tìm x,y.

Giải phương trình: \(x\sqrt {x + 1} + \sqrt {3 - x} = 2\sqrt {{x^2} + 1} \).

Xét tính tăng giảm của dãy u_n = 3ⁿ – n.

Xếp ngẫu nhiên 4 bạn nam và 5 bạn nữ ngồi vào 9 cái ghế kê theo một hàng ngang. Tính xác suất để có được 5 bạn nữ ngồi cạnh nhau?

Cho tam giác ABC và điểm M thỏa mãn:

\(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MA} + 2\overrightarrow {MB} - 3\overrightarrow {MC} } \right|\).

Tập hợp điểm M là gì?

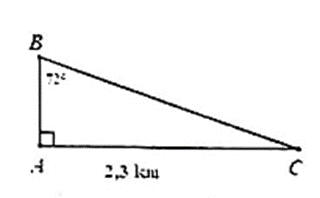
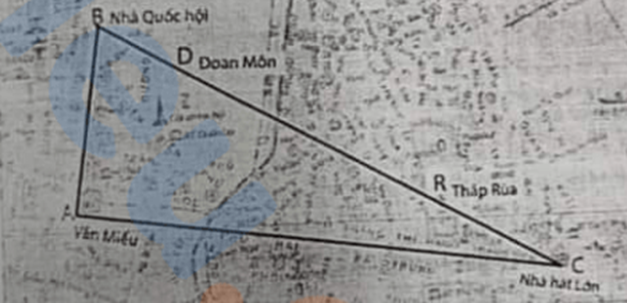
Ở Hà Nội có một tam giác vuông đặc sắc với đỉnh A (Phía đông) là vị trí Văn Miếu, đỉnh B (Phía Bắc) là Nhà Quốc Hội, đỉnh C (Phía Tây) là Nhà hát lớn, trong đó \(\widehat A\)= 90° và \(\widehat B\)= 72°. Con đường thằng từ Văn Miếu đến Nhà hát lớn qua các phố Nguyễn Thái Học, Tràng Thi, Hàng Khay, Tràng Tiền dài khoảng 2,3 km. Hỏi độ dài đường thẳng từ Văn Miếu đến Nhà Quốc hội là bao nhiêu ki–lô–mét? (Kết quả làm tròn đến chữ số thập phân thứ nhất)

Từ các chữ số 0;1;2;3;4;5;6;7 lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau chia hết cho 5, đồng thời luôn có mặt chữ số 2 và chữ số 3 đứng cạnh nhau?

Tìm x biết: –125 + 2(5 – x) = –5.

Cho hàm số bậc nhất: y = (2m – 3)x – 1 (d). Tìm m để:

a. Hàm số là hàm số bậc nhất đồng biến, nghịch biến.

b. Đồ thị của (d) đi qua điểm (–2; 3).

c. Đồ thị của (d) là một đường thẳng song song với đường thẳng 3x – y = 1.

d. Đồ thị của (d) đồng quy với 2 đường thẳng : y = 2x – 4 và y = x + 1.

Một chị bán vải: Lần thứ nhất bán \(\frac{1}{5}\) tấm vải, lần thứ hai bán \(\frac{1}{3}\) tấm vải còn lại. Sau hai lần bán tấm vải còn lại 32 m. Hỏi lúc đầu tấm vải dài bao nhiêu mét ?

Đặt tính rồi tính: 19400 : 435.

Hai xe cùng khởi hành từ thành phố A đến thành phố B với tốc độ lần lượt là v₁ = 20km/h ; v₂ = 10m/s. Hỏi sau 30 phút khoảng cánh giữa hai xe là bao nhiêu?

Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi nếu tổng số tiền lãi là 450 triệu đồng và tiền lãi được chia theo tỉ lệ thuận với số vốn đã đóng?

Cho \(\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2}\). Chứng minh x : 2 = y : 3 = z : 4.

Cho 3 điểm A, B, C thẳng hàng và phân biệt. Trong trường hợp nào thì vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {AC} \)cùng hướng, trường hợp nào thì 2 vectơ đó ngược hướng.

Cho hàm số y = f(x) = mx² + 2(m – 6)x + 2. Có bao nhiêu giá trị nguyên của m để f(x) nghịch biến trên khoảng (–∞; 2)?

Biện luận theo m, số nghiệm của phương trình x³ – 3x² – m = 0.

Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID = IA.

a) Chứng minh ∆ABI = ∆ACI.

b) Chứng minh AC // BD.

c) Kẻ IK vuông góc với AB (K thuộc AB), IH vuông góc với CD (H thuộc CD). Chứng minh IK = IH.

Cho tam giác ABC có AC=2. Gọi M là trung điểm của AB và D là chân đường phân giác trong góc A của tam giác ABC. Hãy tính độ dài AB để trung tuyến CM vuông góc với phân giác AD.

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.

a) Chứng minh: ∆MAB = ∆MDC.

b) Chứng minh: AB // CD và ∆ABC = ∆CDA.

c) Chứng minh: ∆BDC là tam giác vuông.

Cho tanα = 4. Tính giá trị biểu thức P = \[\frac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\].

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

a) Tứ giác MNPQ là hình gì

b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông.

Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \)bằng?

Có bao nhiêu số tự nhiên chia hết cho 4 thoả mãn số đó nhỏ hơn 31,72 và lớn hơn 3,73 ?

Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào 1 bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách xếp cho 3 học sinh nữ ngồi kề nhau?

Hình thang ABCD (AB//CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.

b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.

c) Gọi E là giao điểm của BD và AP. Chứng minh Q, N, E thẳng hàng.

Học sinh khối 5 của một trường tiểu học sinh hoạt động ngoài trời: Nếu chia thành các tổ, mỗi tổ 6 học sinh nam và 6 học sinh nữ thì còn thùa 20 học sinh nam. Nếu chia thành các tổ, mỗi tổ 7 học sinh nam và 5 học sinh nữ thì còn thừa 20 học sinh nữ. Hỏi khối 5 trường tiểu học đó có bao nhiêu học sinh nam ?

Cho \(M = \frac{{2018}}{{2019}} + \frac{{2019}}{{2020}} + \frac{{2020}}{{2021}} + \frac{{2021}}{{2018}}\); \(N = \frac{1}{8} + \frac{1}{9} + \frac{1}{{10}} + ... + \frac{1}{{62}} + \frac{1}{{63}}\). So sánh M và N?

Một cây cau cao 9 m bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu?

Một cửa hàng nhập về 100 cái áo với giá vốn là 200 000 đồng mỗi cái,cửa hàng đã bán 60 cái áo, mỗi cái lời 25% so với giá mua, 40 cái áo còn lại lỗ 5% so với giá mua. Hỏi sau khi bán hết cửa hàng đã lời bao nhiêu tiền?

Một người ăn kiêng muốn trộn hai loại thức ăn A và B, để tạo ra một hỗn hợp chứa ít nhất 50 g protein, ít nhất 130 mg canxi và không quá 550 calo. Giá trị dinh dưỡng của thức ăn loại A và loại B được cho trong bảng sau:

Một lớp có 35 học sinh trong đó có 5 bạn Linh, hỏi có bao nhiêu cách chọn ra 2 bạn để kiểm tra bài cũ trong đó có bạn Linh.

Một người mua một chục bát có giá 40000 đồng. Người đó bán với giá 50000 đồng . Hỏi người đó được lãi bao nhiêu phần trăm so với tiền mua?

Một thợ săn bắn 3 viên đạn vào con mồi. Xác suất để bắn viên đạn trúng mục tiêu là 0,3. Tìm xác suất để người thợ săn bắn trượt mục tiêu.

Một tủ sách khi xếp thành từng bó 8 cuốn, 12 cuốn, 15 cuốn đều vừa đủ bó. Cho biết số sách trong khoảng từ 400 đến 500 cuốn. Tìm số quyển sách đó?

Năm 2010 , gia đình bác Tám thu hoạch được 8 tấn thóc. Năm 2011 gia đình bác tám thu hoạch được 8,5 tấn thóc.

a) Hỏi so với năm 2010 năm 2011 số thóc mà gia đình bác tám thu hoạch tăng thêm bao nhiêu phần trăm?

b) Nếu so với năm 2011 năm 2015 số thóc cũng tăng thêm bấy nhiêu phần trăm thì năm 2015 gia đình bác Tám thu hoạch được bao nhiêu tấn thóc?

Tìm nguyên hàm \(\int {\frac{1}{{\cos x}}dx} \).

Cho tam giác ABC có trung tuyến AM. Đặt \(\overrightarrow a = \overrightarrow {AB} \), \(\overrightarrow b = \overrightarrow {AM} \). Giả sử \(\overrightarrow {AC} = x\overrightarrow a + y\overrightarrow b ;\,\,x,y \in \mathbb{R}\). Tìm cặp số (x; y) tương ứng.

Trong mặt phẳng Oxy, cho tam giác OAB cân tại O. Gọi M(3; 1) là trung điểm cạnh AB. Tìm phương trình ảnh của đường thẳng A qua phép vị tự tâm O, tỉ số k = 4.

Trong số 100 bóng đèn có 4 bóng đèn bị hỏng. Tính xác suất để lấy được 2 bóng tốt.

Tìm các giá trị của tham số m để \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {2m - 1} \right)x - m + 2\) nghịch biển trên (–2; 0).

Tìm một số biết số đó cộng thêm 21 rồi nhân tổng đó với 165 thì được kết quả là 6270.

Tìm số hạng thứ năm trong khai triển \({\left( {x + \frac{2}{x}} \right)^{10}}\) mà trong khai triển đó số mũ của x giảm dần.

Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; –1), B(1; 4) và C(7; 0). Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.

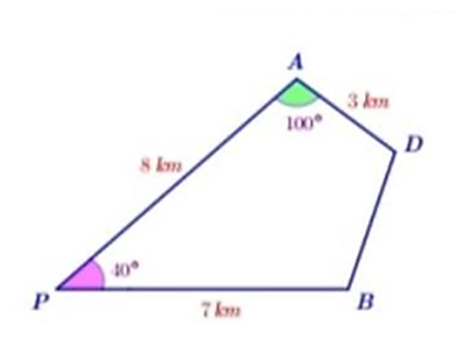
Hai bạn An và Hưng cùng xuất phát từ điểm P, đi theo hai hướng khác nhau và tạo với nhau một góc 40)° để đến đích là điểm D. Biết rằng họ dừng lại để ăn trưa lần lượt tại A và B (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích?

Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau đúng hay sai?

Cho hình thang vuông ABCD với đường cao AB  = 2a, các cạnh đáy AD = a và BC = 3a . Gọi M là điểm trên đoạn AC sao cho \(\overrightarrow {AM} = k\overrightarrow {AC} \). Tìm k để BM ⊥ CD.

Tam giác ABC có \(\widehat A\) = 120° khẳng định nào sau đây đúng?

Cho tam giác ABC có AB = AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a) Chứng minh \(\widehat {EAB}\) = \(\widehat {DAC}\).

b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc \(\widehat {DAE}\).

c) Gỉa sử \(\widehat {DAE} = 60^\circ \). Tính các góc còn lại của tam giác ADE.

Tìm nguyên hàm của sin3x.

Cho tam giác ABC vuông cân tại A, M là trung điểm của AC, trên BM lấy điểm N sao cho NM = MA ; CN cắt AB tại E. Chứng minh:

a) Tam giác BNE đồng dạng với tam giác BAN.

b) \(\frac{{NC}}{{AN}} = \frac{{NB}}{{AB}} + 1\).   

Rút gọn các biểu thức sau:

a) \[\sqrt {x + 1 + 2\sqrt x } \].

b) \(\sqrt {x - 2 + 2\sqrt {x - 3} } \).

c) \(\sqrt {2x - 1 - 2\sqrt {2\left( {x - 1} \right)} } \).

d) \(\sqrt {2x + 1 + 2\sqrt {2x} } \).

Chứng minh rằng: 35x – 14y + 2⁹ – 1 chia hết cho 7.