7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 49)

Tìm giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {\frac{1}{e};\,\,e} \right]\].

Tìm số giao điểm của đồ thị hàm số y = x⁴ − 3x² − 5 và trục hoành.

Tìm giao điểm của đồ thị hàm số y = 2x + 1 (d) và trục hoành.

Cho hàm số y = log₂x. Khẳng định nào sau đây sai?

Một trong các bạn A, B, C và D làm vỡ kính cửa sổ.  Khi được hỏi, họ trả lời như sau:

     A: “C làm vỡ”.

     B: “Không phải tôi”.

     C: “D làm vỡ”.

     D: “C đã nói dối”.

Nếu có đúng một người nói thật thì ai đã làm vỡ cửa số.

Số đo mỗi góc của ngũ giác đều là bao nhiêu?

Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.

Trong các hình sau: hình chữ nhật, hình lục giác đều, hình tam giác. Hình nào không có tâm đối xứng?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = \[a\sqrt 2 \], hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC.

Cho tập A = {0; 1; 2; 3; 4; 5; 6}. Gọi X là tập các số tự nhiên có 5 chữ số khác nhau được lập từ A. Chọn một số từ X, tính xác suất sao cho số được chọn có đúng 3 chữ số chẵn.

Có bao giá trị nguyên của tham số m để phương trình:

4^x – m.2^{x + 1} + 2m² – 5 = 0 có hai nghiệm phân biệt?

Cho phương trình (m + 1)16^x – 2( 2m – 3) . 4^x + 6m + 5 = 0 với m là tham số thực. Tìm tập tất cả các giá trị nguyên của m để phương trình có hai nghiệm trái dấu.

Tìm m để phương trình: cos2x = m – 1 có nghiệm.

Cho hình phẳng (H) giới hạn bởi đường parabol (P): y = x² − x + 2 và tiếp tuyến của đồ thị hàm số y = x² + 1 tại điểm có tọa độ (1; 2). Tính diện tích của hình (H).

Tính tổng S_n = 1² + 2² + ... + n².

Cho tam giác ABC. Chứng minh rằng nếu điểm D thỏa mãn hệ thức: \[\overrightarrow {MA} + 2\overrightarrow {MB} - 3\overrightarrow {MC} = \overrightarrow {CD} \] với M tùy ý thì D là đỉnh của hình bình hành.

Tích tất cả các nghiệm của phương trình \[\log _3^2x - 2{\log _3}x - 7 = 0\] là?

Cho đa giác đều có 20 đỉnh. Số tam giác được tạo từ các đỉnh này là bao nhiêu?

Cho hình nón (N) có bán kính đáy bằng 4, diện tích xung quanh bằng 20π. Tính thể tích khối nón đã cho.

Giải phương trình sau: log₂(x² + x + 2) = 3.

Giải phương trình: $A_x^3+C_x^{x-2}=14x.$

Tìm m để phương trình: x² + mx – 2 = 0 có 2 nghiệm phân biệt x₁, x₂ cùng nhỏ hơn 1.

Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.

Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số:

y = ∣3x⁴ + 8x³ − 6x² − 24x − m∣ có 7 điểm cực trị.

Cho x, y thỏa mãn x – 2y + 2 = 0. Tìm giá trị nhỏ nhất của biểu thức:

\[T = \sqrt {{{(x - 3)}^2} + {{(y - 5)}^2}} + \sqrt {{{(x - 5)}^2} + {{(y - 7)}^2}} \].

Một trường có 50 học sinh giỏi trong đó có 4 cặp anh em sinh đôi. Cần chọn ra 3 học sinh trong số 50 học sinh để tham dự trại hè. Tính xác suất trong 3 em ấy không có cặp anh em sinh đôi?

Một bộ đề thi Olimpic Toán lớp 11 của Trường THPT Kim Liên mà mỗi đề gồm 5 câu được chọn từ 15 câu mức dễ, 10 câu mức trung bình và 5 câu mức khó. Một đề thi được gọi là “Tốt” nếu trong đề thi phải có cả mức dễ, trung bình và khó, đồng thời số câu mức khó không ít hơn 2 . Lấy ngẫu nhiên một đề thi trong bộ đề trên. Tìm xác suất để đề thi lấy ra là một đề thi “Tốt”.

Giải phương trình sau:3^x.2^x+1 = 72.

Giải phương trình sau:\[{5^x}\,.\,{3^{{x^2}}} = 1\].

Tính đạo hàm của hàm số sin²x.

Giải phương trình:sin²x + 2sinx – 3 = 0.

Giải phương trình: \[\sin 3x - \sqrt 3 \cos 3x = 2\sin 2x\].

Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?

Một hộp đựng 15 viên bi khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu.

Tìm tập xác định D của hàm số y = log₂ (x² + 5x − 6).

Tìm tập xác định D của hàm số y = log₂(x³ − 8)¹⁰⁰⁰.

Cho hai điểm cố định A; B. gọi I là trung điểm của AB. Tìm tập hợp các điểm M thoả mãn: \[\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\].

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tính tỉ số \[\frac{{GH}}{{GD}}\].

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[2\sqrt 2 \], cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng?

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác ADFE là hình gì? Vì sao?

Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.

Cho ΔABC vuông tại A, AB = 6 cm, AC = 8 cm. Gọi V₁ là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V₂ là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tính tỉ số \[\frac{{{V_1}}}{{{V_2}}}\].

Cho tam giác ABC, có bao nhiêu điểm M thỏa mãn: \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3?\]

Cho tích phân \[I = \mathop \smallint \limits_0^1 \frac{{{x^7}}}{{{{\left( {1 + {x^2}} \right)}^5}}}dx\], giả sử đặt t = 1 + x². Tính tích phân I.

Cho \[\mathop \smallint \limits_0^1 \left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx = a\ln 2 + b\ln 3\]với a, b là các số nguyên. Chứng minh a + 2b = 0.

Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số \[\overline {abc} \] từ S. Tính xác suất để số được chọn thỏa mãn a ≤ b ≤ c.

Hỏi có bao nhiêu giá trị m nguyên trong [−2017;2017] để phương trình:

log(mx) = 2log(x + 1) có nghiệm duy nhất?

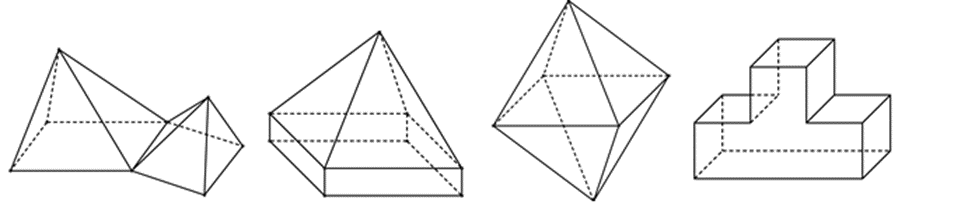
Có bao nhiêu hình đa diện trong các hình dưới đây?

Cho hàm số f(x) thỏa mãn \[f\left( 2 \right) = - \frac{2}{9}\]và f′(x) = 2x[f(x)]² với mọi \[x \in \mathbb{R}\]. Tính giá trị của f(1).

Gọi a và b lần lượt là giá trị lớn nhất và bé nhất của hàm số y = ln(2x² + e²) trên [0; e]. Tính tổng a + b.