7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 47)

Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.

a) Chứng minh ∆ABM = ∆CMA.

b) Chứng minh AK = 2MC.

c) Tính $\widehat{MAK}$.

Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b² + c² – a² = $\sqrt{3}bc$. Tính số đo $\widehat{BAC}$.

Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.

​a) Tính AB, AC, AH.

​b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.

Cho tam giác đều ABC có trọng tâm G và độ dài cạnh a. Tính tích vô hướng $\overrightarrow{AB}.\overrightarrow{AG}$.

Chị Chi mua 50 cái bình hoa với giá mỗi cái là 200000 đồng. Cô bán 20 cái bình lại 20% so với giá vốn, 30 cái còn lại cô bán lỗ vốn 5%. Hỏi việc mua và bán 50 cái bình này chị Chi lãi bao nhiêu tiền?

Giải phương trình: cos³x + cos²x + 2sinx – 2 = 0.

Đặt tính rồi tính 157,25 : 3,7.

Từ A đến B có 3 cách, B đến C có 5 cách, C đến D có 2 cách. Hỏi có bao nhiêu cách đi từ A đến D rồi quay lại A mà không có con đường nào đi từ A đến D?

Có bao nhiêu số tự nhiên có 9 chữ số đôi một khác nhau sao cho có mặt đồng thời bốn chữ số 4; 5; 6; 7 và bốn chữ số đó đôi một không kề nhau?

Có hai địa điểm A, B cùng nằm trên một tuyến đường quốc lộ thẳng. Khoảng cách A và B là 30,5km. Một xe máy xuất phát từ A lúc 7 giờ theo chiều từ A đến B. Lúc 9 giờ, một ô tô xuất phát từ B chuyển động thẳng đều với vận tốc 80 km/h theo cùng chiều với xe máy. Chọn A làm mốc, cho thời điểm 7 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương, Phương trình chuyển động của xe máy là y = 2t² + 36t, trong đó y tính bằng km, t tính bằng giờ. Biết rằng đến lúc ô tô đuổi kịp xe máy thì hai xe dừng lại và vị trí đó cách điểm B là x km. Tính x km?

Hai đội công nhân cùng đào 1 con mương nếu họ cùng làm thì chỉ mất 2 ngày còn nếu làm riêng thì đội 2 nhanh hơn đội 1 là 3 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm bao nhiêu ngày để xong công việc?

Hiện nay anh hơn em 13 tuổi biết sau bảy năm nữa tuổi anh gấp 2 lần tuổi em. Hỏi năm ngoái tuổi anh gấp bao nhiêu lần tuổi em?

Công vào cửa hàng mua 10 quyển vở và 3 bút chì hết 51000 đồng. Dũng mua 5 quyển vở và 6 bút chì cùng loại hết 57000 đồng. Hỏi giá tiền một quyển vở, một cái bút chì là bao nhiêu?

Một thửa đất hình chữ nhật có chu vi là 648m. Chiều rộng kém chiều dài 72m.

a) Tính diện tích thửa đất đó.

b) Một thửa đất hình vuông có chu vi bằng chu vi thửa đất trên. Tính diện tích thửa đất hình vuông.

Cho đa giác đều có 14 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác. Tính xác suất để 3 đỉnh được chọn là 3 đỉnh của một tam giác vuông.

Một vật chuyển động theo quy luật s = $\frac{-1}{3}$t³ + 6t² là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong 9s, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là?

Trong hệ tọa độ Oxy, cho 2 điểm A(2; 3); B(4; –1). Giao điểm của đường thẳng AB với trục tung tại M, đặt $\overrightarrow{MA}=k\overrightarrow{MB}$, giá trị của k là?

Trong mặt phẳng Oxy cho các điểm A(– 1; 2); B(5; 8) điểm M thuộc Ox sao cho tam giác MAB vuông tại A. Tính diện tích tam giác MAB?

Trong một trận lụt ở Hội An, một khách sạn bị nước lụt tràn vào, cần di chuyển cùng một lúc 40 hành khách và 24 vali hành lý. Lúc này chỉ huy động được 8 chiếc ghe lớn và 8 chiếc ghe nhỏ. Một chiếc ghe lớn chỉ có thể chở 10 hành khách và 4 vali hành lý. Một chiếc ghe nhỏ chỉ có thể chở 5 hành khách và 4 vali hành lý. Giá một chuyến ghe lớn là 250 ngàn đồng và giá một chuyến ghe nhỏ là 130 ngàn đồng. Hỏi chủ khách sạn cần thuê bao nhiêu chiếc ghe mỗi loại để chi phí thấp nhất?

Tìm chữ số x, y để $\overline{14x8y}$ chia hết cho 3 và 5.

Vào ngày lễ Black Friday, cửa hàng hoa của chị H quyết định giảm 20% cho 1 bó hoa hướng dương và nếu khách hàng mua 10 bó trở lên thì từ bó thứ 10 trở đi khách hàng sẽ chỉ phải trả nửa giá đang bán hiện tại.

a) Một công ty muốn đặt hoa khai trương nên đã đặt 30 bó hoa. Tính số tiền công ty đó mua biết giá ban đầu của 1 bó là 60000 đồng.

b) 1 khách hàng đã mua hoa hướng dương ở tiệm chị H và tổng số tiền người đó phải trả là 648000 đồng. Hỏi người đó mua bao nhiêu bó?

Viết hỗn số $-3\frac{1}{25}$ sang số thập phân.

Kể tên các khối tròn xoay đã học? Lấy ví dụ trong thực tế.

Tìm ước chung lớn nhất của 11, 13, 17, 19.

Một bể nước cao 2m chứa đầy nước, đáy là hình chữ nhật có chu vi 7,6m, chiều dài hơn chiều rộng 0,8m. Bể đó chứa được lít nước là?

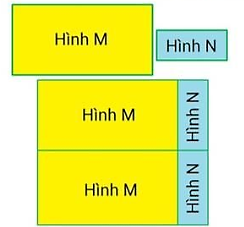
Khi ghép hai hình M và hai hình N lại thì ta được một hình vuông (như hình vẽ) có chu vi là 3232cm. Biết chiều dài hình M lớn hơn chiều rộng hình N là 570 cm. Tìm chu vi hình M?

Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm BC. Phân tích $\overrightarrow{AG}$ theo 2 cạnh của tam giác. Khẳng định nào sau đây đúng?

Cho tam giác ABC vuông tại A , AB = AC. Qua A vẽ đường thẳng d sao cho B và C nằm cùng phía đối với đường thẳng d . Kẻ BH và CK vuông góc với d.

Chứng minh:

a) AH = CK.

b) HK = BH + CK.

Cho tam giác ABC, M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho MC = MN.

a, Chứng minh NB // AC.

b, Trên tia đối tia BN lấy điểm E sao cho BN = BE. Chứng minh: AB = EC.

c, Gọi F là trung điểm của BC. Chứng minh A, E, F thẳng hàng.

Cho tập hợp A = {1; 2; 3; 4; 5}. Có bao nhiêu cặp thứ tự (x; y) biết rằng:

a) x và y đều thuộc A.

b) (x; y) là tập con của A.

c) x và y đều thuộc A sao cho x + y = 6.

Giải phương trình ${\left(\sqrt{4}-x\right)}^2=0$.

Giao điểm của ba đường phân giác gọi là gì?

Tìm các chữ số x,y biết $\overline{x184y}$ chia hết cho 5, chia hết cho 2 dư 1 và chia hết cho 9.

Tìm GTNN, GTLN của A = $\frac{x^2+1}{x^2-x+1}$.

Tìm số bị chia và số chia bé nhất để phép chia đó có thương là 123 và số dư là 44.

Cho tập hợp A = {x ∈ ℝ| x – a| ≤ 2} và B = (– 2; 5]. Biết rằng tập hợp tất cả các giá trị a để A giao B khác rỗng là nửa khoảng (m, n]. Tính S = n + 2m.

Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1, 2, 3.

Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OC = 2cm. Tính AC ?

Cho hình chóp S.ABCD đáy là hình thang (đáy lớn AB). Gọi M, N là trung điểm BC; SB. P thuộc AD sao cho 2PD = PA. Chứng minh MN // (SCD), tìm giao điểm của SA và (MNP).

Một cửa hàng bán trái cây nhập khẩu 500kg Cảm với giá 40000 đồng/1kg. Phí vận chuyển hàng là 4000000 đồng. Giả sử rằng 10% số kg cảm trên bị trong quá trình vận chuyển và số kg cam còn lại được bán hết. Hỏi giá bán của mỗi kg cam là bao nhiêu để công ty có lợi nhuận 20% số với tiền vốn ban đầu?

Một mảnh vườn hình chữ nhật có chu vi là 80m và chiều rộng bằng $\frac{3}{5}$ chiều dài

a) Tính diện tích thửa ruộng đó.

b) Ở giữa mảnh vườn người ta đào một cái ao thả cá. Tính diện tích của ao,biết diện tích của ao chiếm $\frac{2}{5}$ diện tích mảnh vườn.

cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.              

1) Chứng minh AD = BC.        

2) Chứng minh CD vuông góc với AC.          

3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.

Cho hình bình hành ABCD có AB = 2BC. Gọi E và F theo thứ tự là trung điểm của AB, CD.

a) Chứng minh DEBF là hình bình hành.

b) Chứng minh ADFE là hình thoi.

c) Gọi M là giao điểm của DE và AF, N là giao điểm của CE và BF. Chứng minh EMFN là hình chữ nhật.

Có bao nhiêu số nguyên sau khi làm tròn trăm cho kết quả là 6700?

Hai đoạn ống nước có chiều dài lần lượt là 0,8 m và 1,35 m. Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là $\frac{2}{25}$m. Hỏi đoạn ống nước mới dài bao nhiêu mét?

Nêu công thức tính diện tích hình bình hành

Tìm GTNN của P = x² + 2y² + 2xy – 6x – 8y + 2024.

Cho biểu thức Q = $\left(\frac{\sqrt{x}}{1-\sqrt{x}}+\frac{\sqrt{x}}{1+\sqrt{x}}\right)+\frac{3-\sqrt{x}}{x-1}$ với x ≥ 0 và x ≠ 1.

a) Rút gọn Q.

b) Tìm x để Q = – 1.

Cho hình vuông ABCD cạnh a. Tính độ dài vectơ $\overrightarrow{u}=4\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}-2\overrightarrow{MD}$.

Cho hình thang vuông ABCD với đường cao AB  = 2a, các cạnh đáy AD = a và BC = 3a. Gọi M là điểm trên đoạn AC sao cho  $\overrightarrow{AM}=k\overrightarrow{AC}$. Tìm k để BM ⊥ CD

Cho tổng A_n = 1 + 4 + 7+ .... + (3n – 2).

a, Tính A₁, A₂, A₃.

b, Dự đoán công thức A_n và chứng minh bằng quy nạp.

Biết điểm A (– 1; 2) thuộc đường thẳng y = ax + 3(a khác 0). Hệ số góc của đường thẳng trên bằng?

Cho biểu thức $C=\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{2+x}$.

a) Rút gọn C.

b) Tìm x để C = 0.

c) Tìm giá trị nguyên của x để C nhận giá trị dương.

CHo hình vuông ABCD cạnh 6cm. Trên tia đối của AD lấy điểm I sao cho AI = 2cm. IC cắt AB tại K. Tính độ dài IK và IC.

Cho tam giác ABC có  = 60°, a = 10, r = $\frac{5\sqrt{3}}{3}$. Tính R, b, c.

Cho tam giác ABC đều có cạnh 3 cm.

a) Tính diện tích tam giác ABC.

b) Lấy M nằm trong tam giác ABC. Vẽ MI, MJ, MK lần lượt vuông góc với AB, AC, BC. Hãy tính MI + MJ + MK.

Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?

Tính thể tích V của khối lập phương ABCD.A'B'C'D', biết AC' = $a\sqrt{3}$ .

Cho 2 tam giác ABC và A'B'C' lần lượt có các trọng tâm là G và G'. Chứng minh $\overrightarrow{AA\text{'}}+\overrightarrow{BB\text{'}}+\overrightarrow{CC\text{'}}=3\overrightarrow{GG\text{'}}$

Từ đó suy ra điều kiện cần và đủ để 2 tam giác có cùng trọng tâm

Cho đường tròn (O;R). Từ điểm A ở ngoài đường tròn (giả sử OA = 2R) vẽ 2 tiếp tuyến AB, AC với (O) (B, C là 2 tiếp điểm). Chứng minh ΔABC đều.

Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?

Giải phương trình: $\frac{\left(7x+1\right)\left(x-2\right)}{10}+\frac{2}{5}=\frac{{\left(x-2\right)}^2}{5}+\frac{\left(x-1\right)\left(x-3\right)}{2}$.

Tìm tập xác định của hàm số y = $\frac{2\sin x+1}{\tan x}$.

Tính giá trị biểu thức: (– 15).67 – 85.(– 33).

Tìm x, y thỏa mãn $\overline{17x2y}$ chia hết cho 2; 5; 3.

Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ thực tế xí nghiệp 1 vượt mức kế hoạch 10% xí nghiệp 2 vượt mức kế hoạch 15% do đó cả hai xí nghiệp đã làm được 404 dụng cụ tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch.

Tìm giá trị của m để 2x² + 3x + m + 1 > 0 với mọi x ∈ ℝ

Các số chia hết cho 2 có tận cùng là chữ số nào?

Cho hình chữ nhật ABCD có cạnh AB = 5cm và diện tích bằng 30cm2. Lấy M, N lần lượt trên BC và AD sao cho BM = DN = 2cm. Tính diện tích hình thang ABMN.

Cho hình thoi ABCD có cạnh bằng a và có góc A bằng 60°. Tính độ dài của $\left|\overrightarrow{BA}+\overrightarrow{BC}\right|$.

Cho phân thức $\frac{x^2-4x+4}{x^2-4}$.

a) Với giá trị nào của x thì giá trị phân thức được xác định.

b) Tìm giá trị của x để phân thức có giá trị bằng 2.

Cho tam giác ABC (AB = AC). Kẻ đường cao AH cắt đường tròn tâm O ngoại tiếp tam giác tại D.

a) Chứng minh AD là đường kính.

b) Tính $\widehat{ACD}$.

c) Biết AB = AC = 20 cm, BC = 24 cm. Tính bán kính của đường tròn tâm (O)

Cho tam giác ABC vuông tại A có $\widehat{BAC}$ = 60°, kẻ tia Ax song song với BC. Trên Ax lấy điểm D sao cho AD = DC.

a) Tính các góc BAD và DAC.

b) Chứng minh tứ giác ABCD là hình thang cân.

c) Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi.

d) Cho AC = 8cm, AB = 5cm. Tính diện tích hình thoi ABED.

Cho tứ giác ABCD. Xác định điểm O sao cho $\overrightarrow{OB}+4\overrightarrow{OC}=2\overrightarrow{OD}$.

Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C(C≠ A). Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC.

a) Chứng minh AM là đường cao của tam giác ABC và AC² = CM.CB.

b) Chứng minh A, C, I, O cùng nằm trên 1 đường tròn.

c) Chứng minh KM là tiếp tuyến của đường tròn (O).

Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O, R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó.

b) Chứng minh AO vuông góc với BC. Cho biết R = 15 cm, BC = 24cm. Tính AB, OA.

c) Chứng minh BC là tia phân giác của góc ABH

d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. Chứng minh IH = IB.

Cách đổi cm³ sang m³.

Cách làm tròn độ, phút, giây.

Có 9 quả bi sắt giống nhau trong đó có 1 quả nhẹ hơn 8 quả còn lại. Làm thế nào trong 2 lần cân ta phát hiện được quả bi nhẹ hơn ? Giải thích.

Có bao nhiêu số tự nhiên có 2 chữ số mà 2 số đều chẵn?

Giả sử một người có ngân sách tiêu dùng là 1200$ cho hai loại hàng hóa X và Y với giá tương ứng P_X = 100$ và P_Y =300$.

Cho biết hàm tổng lợi ích:            

TU_X = $\frac{-X^2}{3}$ + 10X         

TU_y = $\frac{-Y^2}{2}$ + 20Y

a) Viết phương trình đường ngân sách.

b) Tính lợi ích cận biên của mỗi loại hàng hoá.

c) Tìm kết hợp trong tiêu dùng của người này về hai hàng hóa X và Y sao cho tối đa hóa tổng lợi ích.

Tìm $\lim \frac{2n-\sqrt{4n^2+n}}{n+\sqrt{n^2-2n}}$.

Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2kg nguyên liệu và 30 giờ, đem lại mức lời 40000 đồng. Mỗi kg sản phẩm loại II cần 4kg nguyên liệu và 15giờ, đem lại mức lời 30000 đồng. Xưởng có 200kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?

Một đội xe chuyên chở vật liệu xây dựng.Nếu mỗi chuyến xe chở 2,8 tấn thì phải đi 20 chuyến. Nếu mỗi chuyến chở 4 tấn thì phải đi bao nhiêu chuyến?

So sánh 2021³ và 2020.2021.2022. 

Cho tam giác ABC có $\widehat{B}$ = 60°; $\widehat{C}$ = 45°; BC = a .Tính độ dài cạnh AB và AC?

Cho tam giác ABC vuông tại B có = 30°, BC = a. Gọi I là trung điểm của AC. Hãy tính độ dài vectơ $\overrightarrow{AC},\overrightarrow{AI},\overrightarrow{AB+AC},\overrightarrow{BC}$

Trong một lớp học có 6 bóng đèn, mỗi bóng đèn có xác suất bị cháy là $\frac{1}{4}$. Lớp học đủ ánh sáng nếu có 4 bóng đèn hoạt động. Tính xác suất để lớp học đủ ánh sáng.

Tìm GTLN của biểu thức M = $\frac{x^2-8x+25}{x^2-6x+25}$.

Tổng n số hạng đầu tiên của một cấp số cộng S_n = n² + 4n với n ∈ ℕ^*. Tìm số hạng tổng quát U_n của cấp số cộng đã cho.

Với các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số?

Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Tìm x biết (– 27 + x)(14 – 2x) = 0.

Bác Đức dự định mua loại gỗ giá 200 đồng/ cm² để làm một chiếc bàn. Mặt bàn là một hình thang cân có các đáy lần lượt là 180cm, 240cm và chiều cao 160cm. Hãy tính giúp bác Đức số tiền mua gỗ để đóng mặt bàn đó.

Cho số thực m < 0 và A = (- ∞;9m ), $B=\left(\frac{4}{m};+\infty \right)$ . Tìm điểu kiện m để A ∩ B ≠ ∅.

Cho P = $\frac{8}{-x^2+2x-5}$. Tìm GTNN của P

Qua điểm M ở ngoài đường thẳng a, có có thể vẽ được bao nhiêu đường thẳng đi qua M và vuông góc với đường thẳng a ?

Cho tam giác ABC có AB = 12 cm , AC = 15cm ; BC = 20cm. Trên AC lấy M sao cho AM = 5cm , kẻ MN // BC (N thuộc AB) , kẻ NQ // AC (Q thuộc BC). Tính NA, QB?

$\sqrt{x}+\sqrt{x}$ bằng bao nhiêu?

Một thửa ruộng hình tam giác có cạnh đáy 55,8m và chiều cao bằng 70% độ dài cạnh đáy. Tính diện tích thửa ruộng đó.

Sân nhà bạn An là hình chữ nhật có chu vi là 30m và chiều rộng 5m.

a. Tính diện tích sân nhà bạn An.

b. Bố An muốn dùng những viên gạch hình vuông cạnh là 50cm để lát sân. Vậy bố An cần dùng bao nhiêu viên gạch để lát sân đó?

Trong mặt phẳng tọa độ Oxy cho $\overrightarrow{a}=\left(1;3\right),\overrightarrow{b}=\left(5;7\right)$. Tính tọa độ vectơ $\overrightarrow{u}=3\overrightarrow{a}-2\overrightarrow{b}$.

Trên các cạnh AB, AC của tam giác ABC lần lượt lấy hai điểm M và N sao cho: AM/AB = AN/AC. Gọi I là trung điểm của BC, K là giao điểm của AI với MN. Chứng minh K là trung điểm của MN.

Tìm GTLN, GTNN của biểu thức P = $\frac{x^2-8x+7}{x^2+1}$.

Cho hàm số bậc nhất y = (m - 2)x + 2 - m với m là tham số, có đồ thị là đng thẳng d.

a) Vẽ đường thẳng d trên mặt phẳng tọa độ Oxy với m = 3.

b) Tìm m để hàm số trên đồng biến, nghịch biến.

Cho đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng 1 cạnh là cạnh của (H).

Cho tam giác đều ngoại tiếp đường tròn bán kính 2 cm. Khi đó cạnh của tam giác đều có độ dài bằng bao nhiêu?

Với A, B, C là 3 góc trong 1 tam giác, chứng minh sin A + sin B + sin C = $4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}$.

Tìm x biết $\left|2x+1\right|.\frac{2}{3}=2$.

Cho cấp số cộng (u_n) thỏa mãn u₂ – u₃ + u₅ = 10 và u₁ + u₆ = 17. Tìm u₁ và công sai của cấp số cộng sao cho.

Viết biểu thức bậc ba của 7 + $\sqrt{50}$.

Cho tam giác abc có AB = 2cm, AC = 3cm, $\widehat{A}=60°$. Tính độ dài phân giác góc A

Cho hình chữ nhật ABCD có AB = 8cm , BC = 15cm.

a) Tính độ dài BD.

b) Vẽ AH vuông góc với BD (H thuộc BD). Tính AH.

Cho hình bình hành ABCD.Lấy điểm I trên cạnh AB, điểm K trên cạnh CD sao cho AI = CK.

1. Chứng minh tứ giác AICK là hình bình hành.

2. Qua C kẻ đường thẳng song song với BD cắt AD tại P và cắt AH tại Q. Chứng tỏ C là trung điểm của đoạn PQ.

3. Chứng minh AC, BP, DQ đồng quy.

Một chiếc đồng hồ đánh chuông, số tiếng chuông được đánh đúng bằng số mà kim giờ chỉ tại thời điểm đánh chuông. Hỏi một ngày đêm đồng hồ đó đánh bao nhiêu tiếng chuông?

Hình chiếu vuông góc là hình biểu diễn thu được từ phép chiếu nào?

Hai góc cùng phụ một góc là như thế nào?

Cho (O; R) dây MN vuông góc với OA tại trung điểm H của OA. Các tiếp tuyến với đường tròn (O) tại M và N cắt nhau ở B.

a) Chứng minh rằng 3 điểm O, A, B thẳng hàng.

b) Tam giác BMN là tam giác gì? Vì sao?

c) Tính BM theo R.

Cho hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.

Tìm GTNN của A = x² – 3x + 3.

Cho tam giác ABC vuông tại A có AB = 15, AC = 20.

a) Tính tỉ số lượng giác của B.

b) Vẽ đường cao AH. Tính độ dài các đoạn AH, HB, HC.

c) Gọi D và E lần lượt là trung điểm của BH và AH .Tia CE cắt AD tại M. Chứng minh CM =AM. cos$\widehat{ACM}$.

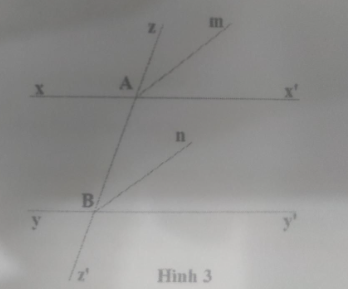
Cho hình 3, biết xx' // yy' ; Am là tia phân giác của góc $\widehat{zAx\text{'}}$, Bn là tia phân giác của góc $\widehat{ zBy\text{'}}$. Chứng minh Am // Bn.

Tìm ƯCLN (16; 40; 176).

Cho tứ giác ABCD. Tìm vị trí của điểm M sao cho $\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{AC}+\overrightarrow{MD}=\overrightarrow{CD}$

Chứng minh nếu n² là số chẵn thì n cũng là số chẵn.

Theo kế hoạch hai tổ được giao sản xuất 600 sản phẩm trong một thời gian đã định. Do cải tiến kĩ thuật nên tổ I đã sản xuất vượt mức kế hoạch 18% và tổ II sản xuất vượt mức kế hoạch 21%. Vì vậy trong cùng thời gian quy định hai tổ đã hoàn thành vượt mức 120 sản phẩm. Tính số sản phẩm được giao của mỗi tổ theo kế hoạch.

Tính giá trị biểu thức: 36.55 – 185.11 + 121.5.

Tìm tập xác định của hàm số y = $tan\left(\frac{\pi }{2}\cos x\right)$.

Giải phương trình sau: sin⁴x + ${\cos }^4\left(x+\frac{\pi }{4}\right)=\frac{1}{4}$.

Quãng đường giữa hai thành phố A và B là 120 km. Lúc 6 giờ sáng, một ô tô xuất phát từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô là một hàm số bậc nhất y = ax + b có đồ thị như hình sau:

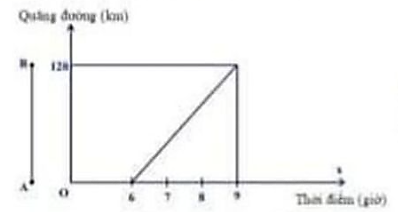
a) Xác định a, b.

b) Lúc 8h sáng ô tô cách B bao nhiêu km?

Tính giá trị của biểu thức A = x² – 6xy + 9y² – 15 tại x = 37, y = – 1.

Tìm giá trị nhỏ nhất của A = a² – 4ab + 5b² + 10a – 22b + 28.

Cho tam giác đều ABC cạnh a. Khi đó $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|$ bằng bao nhiêu?

Họ nguyên hàm của hàm số f(x) = $\frac{1}{\sin x}$ là?

Cách đổi từ vecto chỉ phương sang vecto pháp tuyến

Nhân ngày 20/10 cửa hàng bán túi sách và ví da giảm 30% cho tất cả sản phẩm ai có thẻ VIP giảm 10% trên giá đã giảm.

a) Mẹ bạn An có thẻ VIP thì khi mua 1 cái tui trị giá 500000 đồng phải trả bao nhiêu ?

b) Mẹ bạn An mua thêm 1 cái ví nên phải trả là 693000 đồng. Vậy giá bán đầu của cái bóp là bao nhiêu?

Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?

Cho tam giác abc nội tiếp đường tròn (O) đường kính BC. Chứng minh rằng tam giác ABC là tam giác vuông.

Tính giá trị mỗi chữ số a,b,c biết rằng trong cùng một hàng thì giá trị của chữ số a lớn hơn giá trị của chữ số b là 2 đơn vị của hàng đó và : $\overline{a,bc}+\overline{b,ac}$ = 8,94.

Tìm tập xác định của y = $2\sqrt{x^2-3x+2}$.

Tìm tập xác định của hàm số y = $\frac{\sin x}{\sqrt{3}\sin x+\cos x}$.

Có bao nhiêu giá trị nguyên của tham số m để hàm số:

y =$\sqrt{5-m\sin x-\left(m+1\right)\cos x}$  xác định trên ℝ?

Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần?

Trong mặt phẳng Oxy, cho đường thẳng d: 2x – 5y + 3 = 0. Viết phương trình đường thẳng sao cho d là ảnh của đường thẳng ∆ qua phép quay tâm I(– 1; 2), góc quay – 180°.

Giải phương trình: 2x² – 8x – $3\sqrt{x^2-4x-5}$ = 12.

Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn O (A, B là các tiếp điểm ). Kẻ đường kính AC của đường tròn (O). Gọi H là giao điểm của AB và OM.

a) Chứng minh 4 điểm : O, A, B, M cùng thuộc 1 đường tròn.

b) Tính tỉ số $\frac{OH}{OM}$.

c) Gọi E là giao điểm của CM và đường tròn (O). Chứng minh HE vuông góc với BE.

Chứng minh: sin²x + cos²x = 1 (của 1 góc).

Một chiếc thuyền khởi hành từ bến sông A sau đó 5h20p một chiếc canô từ A đuổi theo và gặp chiếc thuyền cách bến A 20km/h. Hỏi vận tốc chiếc thuyền khi biết ca nô chạy nhanh hơn thuyền 12km/h.

Cô chia kẹo, bánh cho các cháu. Số lượng bánh bằng số lượng kẹo. Nếu chia mỗi cháu 3 bánh thì thừa 2 bánh. Nếu chia mỗi cháu 5 kẹo thì thiếu 28 cái. Tính số kẹo, số bánh và số cháu được chia?

Tìm tập giá trị của hàm số y = tanx?

Tìm x biết x + 17 chia hết cho x + 11.

Cách bấm dấu >, <, lớn hơn hoặc bằng bé hơn hoặc bằng trên máy tính casio 580VNX.

Cách bấm dấu >, <, lớn hơn hoặc bằng bé hơn hoặc bằng trên máy tính casio 580VNX

Cho đoạn thẳng AB và điểm I thỏa mãn $2\overrightarrow{IB}=3\overrightarrow{IA}$. Vẽ hình mô tả đúng giả thiết này?

Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng $\frac{1}{2}$ số đo của cung lớn AB. Tính diện tích của tam giác AOB.

Cho ba điểm A(– 1; 1), B(1; 3), C(– 2; 0).

a) Chứng minh A, B, C thẳng hàng.

b) Tìm các tỉ số mà A chia đoạn BC, B chia đoạn AC và C chia đoạn AB.

Một người mua 72,8 kg gạo nếp và gạo tẻ.Biết rằng số gạo nếp bằng $\frac{3}{5}$ số gạo tẻ. Hỏi người đó mua bao nhiêu ki - lô - gam gạo mỗi loại?

Hai xạ thủ Thế và Vinh cùng bắn vào mục tiêu một cách độc lập. Xác suất bắn trúng của xạ thủ Thế là 0,7. Biết rằng xác suất có ít nhất một người bắn trúng bia là 0,94. Xác suất bắn trung của xạ thủ Vinh là:

Cho biểu thức A = $\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{\sqrt{x}-1}{\sqrt{x}+1}+\frac{3\sqrt{x}+1}{1-x}$  với x ≥ 0 và x ≠ 1.

a) Rút gọn A.

b) Tìm GTNN của A.

Hai tấm vải dài 124m. Hỏi mỗi tấm vải dài bao nhiêu mét? Biết rằng tấm vải thứ nhất dài hơn tấm vải thứ hai 18m.

Cho đường tròn (O; R) và 1 điểm A sao cho OA =$R\sqrt{2}$ . Vẽ tiếp tuyến AB, AC với đường tròn 1 góc  $\widehat{xOy}$= 45° cắt đoạn thẳng AB và AC lần lượt tại D và E.

Chứng minh:

a) DE là tiếp tuyến của đường tròn (O).

b) $\frac{2}{3}R<DE<R$.

Rút gọn biểu thức: A = $\frac{x-3}{x}-\frac{x}{x-3}+\frac{9}{x^2-3x}$.

Trong 1 cái lọ chứa n cái kẹo (n ∈ ℕ^*). 2 bạn Lan và Khoa chơi một trò chơi như sau: 2 người luân phiên lấy kẹo từ trong lọ ra, mỗi lần đc lấy 1, 2, 3, 4, 5 cái. Người lấy được cái kẹo cuối cùng trong lọ là người chiến thắng. Nếu Lan đi trước:

a) Với n = 10, hãy chỉ ra cách chơi của Lan để Lan là người thắng.

b) Với n = 74, hãy chỉ ra cách chơi của Lan để Lan là người thắng.

Nêu cách tính bán kính đường tròn ngoại tiếp.

Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của (O) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N.

a) Chứng minh DC = DN.

b) Chứng minh AC là tiếp tuyến của đường tròn tâm O.

Cho tam giác ABC đều cạnh a. Tính độ dài vectơ $\overrightarrow{AB}-\overrightarrow{AC};\overrightarrow{AB}+\overrightarrow{AC}$. 

Cho tam giác ABC. Chứng minh rằng $\overrightarrow{AB}.\overrightarrow{AC}=\frac{1}{2}\left(A{B}^2+A{C}^2-B{C}^2\right)$.

Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao so với mặt đất sau đó giây nó đạt độ cao và sau giây nó ở độ cao. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?

Có ba chiếc hộp mỗi hộp đựng 2 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 1 viên bi xanh?

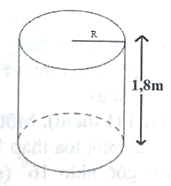
Bác Tư du định mua một bồn nước inox hình trụ có dung tích V = 2500 lít và chiều cao h = 1,8m để đựng nước. Để đưa bồn đó lên vị trí cần đặt phải qua một cửa hình chữ nhật có kích thước 1,4m × 2m. Em tính xem có thể đưa bồn đó qua cửa hình chữ nhật đó được không? Biết bán kính R của 1,8m hình tròn đáy của hình trụ được tính theo công thức R =$\sqrt{\frac{V}{\pi .h}}$ (xem hình vē).

Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.

a) Chứng minh rằng: AD = MN; $\widehat{MDN}$= 90°.

b) Gọi AH vuông góc BC tại H. Chứng minh rằng: $\widehat{MHN}$ = 90°.

c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?

Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?

Giải hệ phương trình: $\left\{\begin{array}{l}{x}^2+y^2=65\\ \left(x-1\right)\left(y-1\right)=18\end{array}\right.$.

Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với mọi điểm I ta có: $\overrightarrow{IG}=\frac{1}{3}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)$

Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại