7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 38)

Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn a + b + c = 0. Chứng minh rằng: \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\) là bình phương của một số hữu tỉ.

Cho biểu thức:\[A = \sqrt {\frac{{{{\left( {{x^2} - 3} \right)}^2} + 12{x^2}}}{{{x^2}}}} + \sqrt {{{\left( {x + 2} \right)}^2} - 8x} \].

a) Rút gọn A.

b) Tìm các giá trị nguyên của x để giá trị của A là một số nguyên.

Cho biểu thức: \(P = \left( { - \frac{2}{3}{x^2}{y^3}{z^2}} \right){\left( { - \frac{1}{2}xy} \right)^3}{\left( {x{y^2}z} \right)^2}\).

a) Rút gọn biểu thức P.

b) Tìm bậc và hệ số biểu thức B.

c) Tìm giá trị các biến để P £ 0.

Chứng minh:\(\sqrt {{a^2} + {b^2}} + \sqrt {{c^2} + {d^2}} \ge \sqrt {{{\left( {a + c} \right)}^2} + {{\left( {b + d} \right)}^2}} ,\;\forall a,\;b,\;c,\;d \in \mathbb{R}\).

Cho tập A = {0; 1; 2; 3; 4; 5}, từ A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau, trong đó nhất thiết phải có chữ số 0 và 3.

Từ các chữ số 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên có năm chữ số khác nhau và nhất thiết phải có chữ số 1 và 5?

Cho một cấp số cộng (u_n) có u₁= 5 và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát u_n.

Cho dãy số (u_n) là một cấp số cộng, biết u₂ + u₂₁ = 50. Tính tổng của 22 số hạng đầu của dãy.

Tìm số mặt cầu chứa một đường tròn cho trước.

Có bao nhiêu mặt cầu chứa một đường tròn cho trước?

Tìm x, biết: 4x + 5 chia hết cho x + 1.

Tìm x biết: 4x − 5 chia hết cho x – 1.

Cho \(\left( {x + \sqrt {{x^2} + 3} } \right)\left( {y + \sqrt {{y^2} + 3} } \right) = 3\). Tính giá trị của biểu thức E = x + y.

Hệ phương trình \(\left\{ \begin{array}{l}{x^2} + \sqrt x = 2y\\{y^2} + \sqrt y = 2x\end{array} \right.\) có bao nhiêu cặp nghiệm (x; y) ¹ (0; 0)?

Cho hình chóp đều S.ABCD có AC = 2a, mặt bên (SBC) tạo với mặt đáy ( ABCD) một góc 45°. Tính thể tích V của khối chóp S.ABCD.  

Cho mặt phẳng (P) và hai đường thẳng song song a và b. Khẳng định nào sau đây đúng? 

Cho một mặt phẳng (P) và hai đường thẳng song song a, b. Mệnh đề nào sau đây là sai?

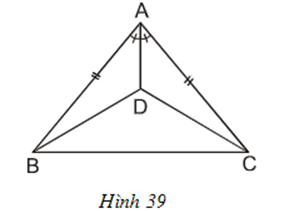
Cho hình 39.

a) Chứng minh ΔABD = ΔACD.

b) So sánh góc DBC và góc DCB.

Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.

a) Chứng minh DABD =DACD.

b) Chứng minh rằng AM = 2.BD.

c) Tính số đo \[\widehat {MAD}\].

Tính giá trị biểu thức: B = (3x + 5)(2x − 1) + (4x − 1)(3x − 2) với |x| = 2.

Rút gọn và tính giá trị:A = (3x + 5)(2x − 1) − (1 − 4x)(3x + 2) tại |x| = 2.

Khi quay 1 hình tam giác vuông một vòng quanh một cạnh góc vuông cố định ta được hình:

Chọn đáp án đúng điền vào chỗ trống: “Khi quay ……… một vòng quanh một cạnh góc vuông cố định, ta được hình nón”  

Một nhà máy sản xuất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là?

Tìm m để phương trình log² x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1).

Tìm m để phương trình \(\log _2^2\left( x \right) - {\log _2}\left( {{x^2}} \right) + 3 = m\) có nghiệm x Î [1; 8].

Tìm tất cả các giá trị của b để hàm số y = x² + 2(b + 6)x + 4 đồng biến trên khoảng (6; +∞).

Tìm tất cả các giá trị của tham số m để hàm số y = x³ − 2mx² + m²x + 2 đạt cực tiểu tại x = 1.

Tính \(x = \sqrt[3]{{2 - \sqrt 3 }} + \sqrt[3]{{2 + \sqrt 3 }}\).

Rút gọn biểu thức: \(A = \sqrt {2 + \sqrt 3 } + \sqrt {2 - \sqrt 3 } \).

Xác định hàm số bậc hai y = ax² − x + c biết đồ thị hàm số đi qua A(1; −2) và B(2; 3).

Tìm công thức hàm số bậc hai, biết:

a) Đồ thị hàm số đi qua 3 điểm A(1; −3), B(0; −2), C(2; −10).

b) Đồ thị hàm số có trục đối xứng là đường thẳng x = 3, cắt trục tung tại điểm có tung độ bằng −16 và một trong hai giao điểm với trục hoành có hoành độ là −2.

Cho \(\left( {x + \sqrt {{x^2} + 3} } \right)\left( {y + \sqrt {{y^2} + 3} } \right) = 3\). Tính giá trị của biểu thức E = x + y.

Hệ phương trình \(\left\{ \begin{array}{l}{x^2} + \sqrt x = 2y\\{y^2} + \sqrt y = 2x\end{array} \right.\) có bao nhiêu cặp nghiệm (x; y) ¹ (0; 0)?

Cho \[\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\]. Tính x + y.

Cho 2 số thực x, y thỏa mãn \[\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\]. Tìm giá trị nhỏ nhất của biểu thức M = 10x⁴ + 8y⁴ − 15xy + 6x² +5y² + 2017.

Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình bên.

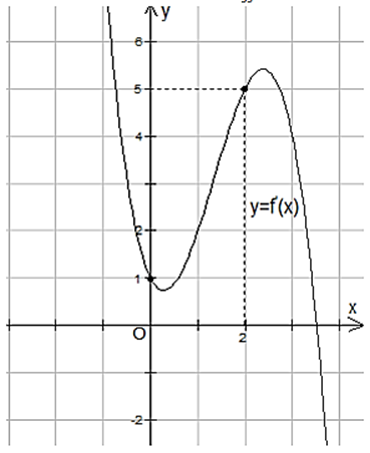
Khẳng định nào sau đây là đúng?

Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị ở hình bên. Số nghiệm dương phân biệt của phương trình \(f\left( x \right) = - \sqrt 3 \) là: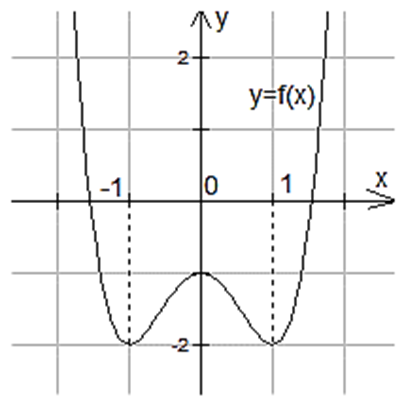

Giải phương trình 2x² + y² − 6x + 2xy − 2y + 5 = 0.

Giải phương trình 2x² + y² − 2xy − 6x + 9 = 0.

Cho hai số hữu tỉ \(\frac{a}{b}\) và \(\frac{c}{d}\;\left( {b > 0,\;d > 0} \right)\). Chứng tỏ rằng:

a) Nếu \[\frac{a}{b} < \frac{c}{d}\] thì ad < bc.

b) Nếu ad < bc thì \[\frac{a}{b} < \frac{c}{d}\].

Hình thang ABCD có đáy AB, CD.

a) Cho biết AD // BC. Chứng minh rằng AD = BC, AB = CD.

b) Cho biết AB = CD. Chứng minh rằng AD // BC, AD = BC.

Cho biểu thức: M = (x − 3)³ − (x + 1)³ + 12x(x − 1).

a) Rút gọn M.

b) Tính giá trị M tại \(x = - \frac{2}{3}\).

c) Tìm x để M = −16.

Rút gọn: (x − 3)³ − (x + 1)³ + 12x(x − 1).

Cho a, b, c Î ℝ thỏa mãn a² + b² + c² = a³ + b³ + c³ = 1.

Tính a²⁰¹² + b²⁰¹³ + c²⁰¹⁴.

Cho a; b; c là các số thực không âm có: a + b + c = 1. Chứng minh rằng:

3(a³ + b³ + c³) ³ a² + b² + c².

Cho a + b + c = 1, a² + b² + c² = 1, a³ + b³ + c³ = 1. Tính M = abc.

Phân tích thành nhân tử:

a) A = ab(a − b) + bc(b − c) + ca(c − a)

b) B = a(b² − c²) + b(c² − a²) + c(a² − b²)

c) C = (a + b + c)³ − a³ − b³ − c³

Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1; 17]. Tính xác suất để ba số được viết ra có tổng chia hết cho 3.

Giải bất phương trình (n Î ℕ): \(\frac{{C_{n + 1}^2}}{{C_n^2}} \ge \frac{3}{{10}}n\).

Tìm số nguyên dương n thỏa mãn:

\(C_n^0 + 2C_n^1 + {2^2}C_n^2 + {2^3}C_n^3 + ... + {2^{n - 2}}C_n^{n - 2} + {2^{n - 1}}C_n^{n - 1} + {2^n}C_n^n = 243\).

Cho a, b, c > 0 thỏa mãn: a + b + c = 1. Chứng minh rằng:

\(\sqrt {5a + 1} + \sqrt {5b + 1} + \sqrt {5c + 1} \le 2\sqrt 6 \).

Cho a, b, c > 0. Chứng minh rằng:

\(\sqrt {\frac{{{a^3}}}{{5{a^2} + {{\left( {b + c} \right)}^2}}}} + \sqrt {\frac{{{b^3}}}{{5{b^2} + {{\left( {c + a} \right)}^2}}}} + \sqrt {\frac{{{c^3}}}{{5{c^2} + {{\left( {a + b} \right)}^2}}}} \le \sqrt {\frac{{a + b + c}}{3}} \).

Cho x² + y² + xy = 1. Tìm GTNN, GTLN của A = x² − xy + 2y².

Cho x, y không âm thỏa mãn: x² + y² = 2. Tìm GTNN, GTLN của

\(A = \frac{{{x^2} + {y^2} + 1}}{{xy + 1}}\).

Cho tam giác vuông ABC vuông tại A có BC = 20 cm; AC = 12 cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là bao nhiêu?

Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi ℓ_a là độ dài đoạn phân giác trong góc \(\widehat {BAC}\). Tính ℓ_a theo b và c.

Cho tam giác ABC có A(3; 3), B(2; 1), C(5; 1). Tìm tọa độ trực tâm H của tam giác ABC.

Cho tam giác ABC có A(7; 3), B(7; 1), C(10; 1). Tìm tọa độ trực tâm H của tam giác ABC.

Tìm x, biết: \(x = \sqrt {5 + \sqrt {13 + \sqrt {5 + \sqrt {13 + ......} } } } \).

Cho a, b, c là các số dương tùy ý. Chứng minh rằng:

\[\frac{{bc}}{{b + c + 2a}} + \frac{{ca}}{{c + a + 2b}} + \frac{{ab}}{{a + b + 2c}} \le \frac{{a + b + c}}{4}\].

Cho a, b, c là số thực dương thỏa mãn a + b + c = 2. Tìm giá trị lớn nhất của: \[P = \frac{{ab}}{{\sqrt {ab + 2c} }} + \frac{{bc}}{{\sqrt {bc + 2a} }} + \frac{{ca}}{{\sqrt {ca + 2b} }}\].

Giải phương trình: sin² 2x − sin 2x − 2 = 0.

Giải phương trình: sin 2x + sin² x = 1

Hãy chọn câu đúng: 

Trong các mệnh đề sau, mệnh đề nào đúng?

Hình chiếu bằng của hình lăng trụ tam giác đều là hình gì?

Hình chiếu bằng của hình lăng trụ tam giác đều là hình gì nếu mặt đáy song song với mặt phẳng chiếu bằng bao nhiêu?

Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được:

Chọn khẳng định sai trong các khẳng định sau:  

Cho các khẳng định:

(I): Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.

(II): Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.

(III): Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng thì chúng thẳng hàng.

Số khẳng định sai trong các khẳng định trên là:

Tìm GTLN và GTNN của biểu thức: \[A = \frac{{{x^2} - x + 1}}{{{x^2} + x + 1}}\].

Tìm GTLN và GTNN của biểu thức: \[A = \frac{{{x^2} + 1}}{{{x^2} - x + 1}}\].

Tìm số nguyên n sao cho n + 2 chia hết cho n − 3.

Tìm số nguyên n lớn nhất sao cho n + 2 chia hết cho n − 3.

Trong mặt phẳng Oxy cho A(−2m; −m), B(2m; m). Với giá trị nào của m thì đường thẳng AB đi qua O? 

Trong mặt phẳng Oxy, cho A (m − 1; −1), B (2; 2 − 2m), C (m + 3; 3). Tìm giá trị m để A, B, C là ba điểm thẳng hàng.

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4); B(3; 2); C(5; 4). Tính chu vi P của tam giác đã cho.

Hình vuông ABCD có A(1; −3), B(5; 4). Tìm tọa độ các đỉnh còn lại.

Tìm GTNN của biểu thức:

a) A = x² − 6x + 11;

b) B = x² − 20x + 101.

Tìm GTNN của biểu thức: A = −x² + 6x – 11.

Khai triển (1 + 2x)¹⁰ = a₀ + a₁x + a₂x² + … + a₁₀x¹⁰. Tìm a₇.

Tìm hệ số của x⁷ trong khai triển biểu thức f (x) = (1 − 2x)¹⁰.

Cho hai số hữu tỉ \(\frac{a}{b}\) và \(\frac{c}{d}\;\left( {b > 0,\;d > 0} \right)\). Chứng tỏ rằng:

a) Nếu \[\frac{a}{b} < \frac{c}{d}\] thì ad < bc.

b) Nếu ad < bc thì \[\frac{a}{b} < \frac{c}{d}\].

Hình thang ABCD có đáy AB, CD. Cho biết AB = CD. Chứng minh rằng AD // BC, AD = BC.

Tính giá trị biểu thức A = (x − 3)² − (x + 1)² + 12x(x − 1) với \(x = - \frac{1}{2}\).

Cho biểu thức: A = (x − 3)² − (x + 1)² + 12x(x − 1).

a) Rút gọn A.

b) Tính giá trị của A tại \(x = - \frac{2}{3}\).

c) Tìm x để A = −16.

Cho bất phương trình 2x + 3y − 6 £ 0 (1). Chọn khẳng định đúng trong các khẳng định sau:

Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\] chứa điểm nào sau đây?

Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Tìm số các cách để chọn những màu cần dùng.

Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình gì?